点集拓扑 3.6 紧性
2023-11-20 21:07:22 新建
波莱尔有限覆盖定理
设 是闭区间 的一个(无限)开覆盖,则必可从 中选择有限个开区间来覆盖 。
实数连续性定理中的 Borel 有限覆盖定理所揭示的**闭区间**的性质, 在一般拓扑学中称为紧性.
紧性在拓扑学的研究中占据核心的地位, 其思想与方法是一般拓扑学发展的重要源泉.
定义 3.6.1 覆盖
设 是拓扑空间, 是 的子集族.
- 如果 , 则称 覆盖 , 或称 是 的覆盖.
- 如果 的每个元素是 的开子集, 则称 是 的开覆盖.
设 是 的覆盖.
- 如果 的子族 也是 的覆盖, 则称 是 的子覆盖.
- 如果 的元素还是有限 (或可数) 的, 则称 是 的有限 (或可数) 子覆盖.
定义 3.6.2 紧空间
设 是拓扑空间, 是 的子空间
- 如果 的**每个**开覆盖**都有**有限子覆盖, 则称 是紧空间.
- 如果 作为拓扑空间是紧空间, 则称 是 的紧子集.
// 此时 可以不是紧空间
如何判断不是紧空间
定义要求 “**每个**开覆盖**都有**...” ,所以**只要举一个**开覆盖没有就行了,如下例子所示
例 3.6.1 几个简单的例子
- 平庸空间是紧空间.
- 离散空间是紧空间当且仅当它是有限的空间.
- 实空间 不是紧空间.
- 因为 是 的开覆盖,
- 但 的**任意**有限子族 都不能覆盖 .
- 因此, 没有有限子覆盖.
- 作为 的子空间是紧的(是 的紧子集).
- 设 是 的任意开覆盖, 存在 使得 .
- 存在 , 使得当 时有 .
- 对 , 存在 使得 .
- 令 , 则 是 的有限子覆盖.
定理 3.6.1 【序拓扑跳过】
若 是具有上确界性质的全序集, 则序拓扑空间 的每个闭区间是紧的.
推论
由此, 实空间 中的每个闭区间是紧的.
在例 3.6.1 的 (4) 中, : 作为 的子空间是紧的, 但实空间 不是紧空间。所以我们想知道:紧空间的子空间是否一定是紧空间呢?这就是紧空间的遗传性问题
例子 紧空间的子空间不一定是紧的.
在例 3.6.1 的 (4) 中, : 是紧的, 但它的子空间 是无限的离散空间, 所以不是紧的.
所以紧性不具有遗传性,此时我们想知道紧空间有没有哪一类子空间一定是紧空间呢?
下面研究紧子集的性质
定义 子空间覆盖
设 是拓扑空间 的子空间.
- 如果 是 的子集族且 , 则称 覆盖 .
拓扑空间的一个子集 是紧子集意味着每个由子空间 中的开集构成的 的开覆盖有一个有限子覆盖那么由 中的开集构成的每个 中的开覆盖是否有有限子覆盖?
引理 3.6.1
如果 是拓扑空间 的子空间,
- 则 是紧的当且仅当由 中开集组成的 的每个覆盖都有有限子覆盖.
证明的关键是区分 的地位:是视为全空间;还是视为 的子空间
- 是紧的: 是全空间
- 中开集组成的 的每个覆盖: 是全空间, 是 的子空间;这个覆盖是子空间覆盖
- ...都有有限子覆盖: 是全空间, 是 的子空间
证明
- 设 是紧的且 是由 中开集组成的 的覆盖,
- 那么 : 是子空间 的开覆盖.
// 这个开覆盖是把 视为全空间,所以下面就能利用紧空间的定义 - 由 是紧的, 得 有有限子覆盖 .
// 这个有限子覆盖是把 视为全空间 - 于是, 的有限子族 覆盖 .
// 这个有限子覆盖是把 视为全空间
- 那么 : 是子空间 的开覆盖.
- 设 是子空间 的开覆盖.
// 这个开覆盖是把 视为全空间,下面要证 是紧的,只要证明这个开覆盖有有限子覆盖- 对每个 , 存在 中的开集 使得 .
// 这步由子空间的定义可得 - 因此, 是由 中开集组成的 的覆盖.
// 这个覆盖是把 视为全空间 - 根据假设, 的某有限子族 覆盖 .
// 这个子覆盖是把 视为全空间 - 于是, 的有限子族 覆盖 .
// 这个子覆盖是把 视为全空间 - 故 是紧的.
- 对每个 , 存在 中的开集 使得 .
随笔
有了这个引理,谁是全空间已经不那么重要了,相当于子空间覆盖和全空间覆盖画了等号
定理 3.6.2
紧空间的每个闭子集是紧的.
证明
- 设 是紧空间 的闭子集.
- 若 是由 中开集组成的 的覆盖,
// 构造使用 引理 3.6.1 的条件 - 则 是 的开覆盖.
// 是 的闭子集,所以 是开集 - 由 的紧性, 它存在有限子覆盖, 记为 .
- 因此, . 于是, 有有限子族覆盖 .
- 根据引理 3.6.1, 是紧的.
- 若 是由 中开集组成的 的覆盖,
通过前面的学习,我们知道紧空间的子空间不一定是紧的。但是紧空间中的每个闭子集都是紧子集,那么紧空间的紧子集是否一定是闭子集?
例子 紧子集不一定是闭的.
让 是无限集, 赋予有限补拓扑, 则 是 的紧空间 (见习题 3.6.1). 显然, 的每个子空间也是有限补空间 (见习题 2.4.5), 所以也是紧空间, 但是 的真闭子集都是有限集. 从而 的紧子集不一定是闭的.
即满足 分离性公理的紧空间中的紧子集不一定是闭集,那么什么条件下紧子集是闭子集?
我们自然去考虑满足 分离性公理的空间中的紧子集是否是闭集。
引理 3.6.2
如果 是 Hausdorff 空间 中不相交的紧子集,
- 则存在 的开集 使得 且 .
证明
- 取定 . 对任意的 , 则 .
- 由于 是 Hausdorff 空间, 存在 中不相交的开集 及 使得 和 .
- 令 , 则 是 中的开集族且覆盖 .
- 由引理 3.6.1, 存在 的有限子族 覆盖 .
- 令 ,
- 则 和 是 中分别包含 与 的不相交开集.
- 现在, 对每个 ,
- 由上段所证, 存在 中不相交的开集 使得 .
- 令 , 则 是 中开集组成的 的覆盖.
- 由 的紧性, 的某有限子族 覆盖 .
- 令 ,
- 则 和 是 的不相交开集, 分别包含 和 .
// 这里的不相交,关键在于一个取并一个取交,任意 与 不相交,否则必与 相交,矛盾。
定理 3.6.3
Hausdorff 空间的每个紧子集是闭的.
证明
- 先设 是 Hausdorff 空间 的紧子集.要证 是闭的,即证 是开的。
- 对每个 ,由定义易知单点集 是紧的。
- 由引理 3.6.2,存在 中不相交的开集 分别包含 和 .
// 这里画个图 - 于是,.
- // 即对任意的 都存在开集 使得
- // 即 是它的每一点的领域。
- 由定理 2.1.1, 是开集, 从而 是闭集.
// 定理 2.1.1:拓扑空间 的子集 是开集当且仅当 是它的每一点的邻域.
// 邻域定义:设 是拓扑空间, . 如果存在开集 使得 , 则称 是 的邻域.
所以我们可以得到下面这个简单的结论
紧空间:闭子集 紧子集
Hausdorff 空间:闭子集 紧子集
引理 3.6.2 中 Hausdorff 空间中不相交的紧子集 都能被空间中两个不相交的开集分离,这个做法和正规空间类似,所以我们想知道:紧的 Hausdorff 空间和正规空间有什么关系。
定理 3.6.4
紧的 Hausdorff 空间是正规的.
证明
- 先设 是紧的 Hausdorff 空间,要证 是正规的。
- 由正规的定义,再设 , 是 的任意两个不相交的闭集
- 所以 , 是紧空间 的闭子集
- 所以由定理 3.6.2 得,, 是紧子集
- 所以 , 是 Hausdorff 空间 的不相交的紧子集
- 所以存在 的开集 使得 且 .
- 所以由正规的定义知, 是正规的。
// 正规:空间中任意两个不相交的闭集 都能被空间中两个不相交的开集分离.
// 定理 3.6.2:紧空间的每个闭子集是紧的.
// 引理 3.6.2:Hausdorff 空间中不相交的紧子集 都能被空间中两个不相交的开集分离.
下面讨论紧空间的映射性质.
定理 3.6.5 关于紧空间的映射定理
紧空间的连续像是紧的, 即连续映射保持紧性.
证明
- 先设 是紧空间且 是连续映射,要证连续像 是紧的
- 再设 是由 中的开集组成的 的覆盖,即
- 所以
- 又因为 连续,所以对任意的 , 是开的。
- 所以 是 的开覆盖.
- 由 的紧性,它的某有限子族 覆盖 .
- 所以 ,所以
- 从而, 的有限子族 覆盖 ,所以 是紧的。
证明【上面的证法应该是对的,老师说直接假设满射更简单】
- 先设 是紧空间且 是连续满映射,要证连续像 是紧的
- 再设 是 的开覆盖,即
- 所以
- 又因为 连续,所以对任意的 , 是开的。
- 所以 是 的开覆盖.
- 由 的紧性,它的某有限子族 覆盖 .
- 所以 ,所以
- 从而, 的有限子族 覆盖 ,所以 是紧的。
由此, 紧性是拓扑性质.
// 书P20 拓扑性质=同胚不变性质,因为同胚映射一定是连续的,所以在连续映射下保持不变的性质一定是拓扑不变性;连续的双射不一定是同胚。
定理 3.6.6 最值定理
设函数 连续, 是序拓扑空间. 如果 是紧空间, 则 中存在点 和 , 使得对任意 , 有 .
证明
// 序拓扑空间改成实空间也是一样的证明
- 设 要证 有最值
- 由定理 3.6.5, 是 的紧子集
- 再设
- 因为 没有最大元,
- 所以对 , s.t. ,
- 即 s.t.
- 所以 ,所以 是 的开覆盖( 是全集)
- 由 是紧的,所以有有限子覆盖 ,其中
- 由开覆盖 的定义 可得
- 设 , 则 .
- 有限个 数 取最大,那这最大值 肯定还在 中
- 我们又知道 ,,所以 .
- 但 .
- 我们知道 是最大的,所以
- 区间右边是开的,所以取不到,不属于
- 这与 覆盖 矛盾.
- 故 有最大元. 同理, 有最小元.
- 设 和 分别是 的最小元和最大元,
- 则存在 , 使得 和 .
- 因此, 对任意的 , 有 .
受上面启发,我们想知道紧空间到 Hausdorff 空间的连续映射有什么性质。
定理 3.6.7
紧空间到 Hausdorff 空间的连续映射是闭映射.
证明
- 先设 是连续映射, 其中 是紧空间, 是 Hausdorff 空间,要证 是闭映射
- 再设 是 的任意一个闭集,即证 是 的闭集。
- 根据定理 3.6.2, 则 是 的紧集.
- 由于 连续, 根据定理 3.6.5, 是 的紧集.
- 因为 是 Hausdorff 空间, 根据定理 3.6.3, 在 中是闭的,
- 所以 是闭的.
// 定理 3.6.2:紧空间的每个闭子集是紧的.
由此可知, 例 2.4.4 中的函数 是闭映射.
根据同胚映射的性质(书 P41 定理2.6.3):既单且满的开(或闭)的连续映射。
有以下推论:
推论 3.6.1
紧空间到 Hausdorff 空间的连续双射是同胚.
下面讨论紧空间的有限可积性。
随笔
同样的,先讨论两个拓扑的积空间,我们一般就是将他们画成坐标平面的形式:
对于一般的开集,是个面,像左边这样,而 就是像右边这样,里面包含一杠。
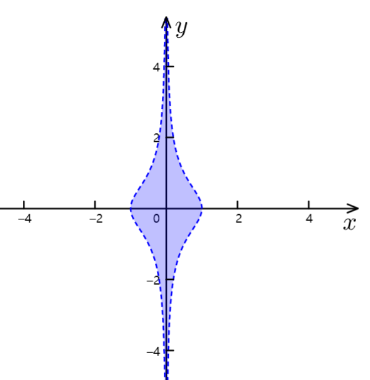
引理 3.6.3 管形引理
设 是拓扑空间, 是紧空间, . 如果积空间 中的开集 , 则存在 中包含 的开集 , 使得 .
证明
- 对任意的 , 有 .
- 又因为 是 的开集,由定理2.2.1,存在 的基,使得 ,其中 和 分别是 与 的开集。
- 集族 是 的开覆盖.
- 由 的紧性, 有有限的子覆盖 .
- 令 , 则 是 中含 的开集.
// 是紧空间用在这,保证 为有限交,才能为开集 - 且 ,事实上,对任意的 ,因为 覆盖 ,所以存在 ,使得 ,又因为 ,所以 .
图 3.6.1
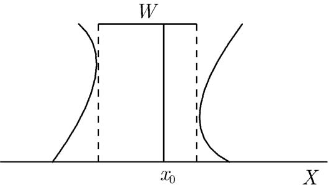
例子 管形引理中, 拓扑空间 的紧性是重要的.
在欧氏平面 中, 取
则 是 中包含 的开集. 但不存在 中包含 0 的开集 , 使得 .
// 纵轴 不是紧的,那就需要取极限 为闭集。
// 这个例子应该严格证明,我没写
定理 3.6.8
紧空间性质是有限可积性.
证明
- 仅证两个紧空间的积空间是紧空间 (类似定理 3.2.6 的说明).
- 设 和 都是紧空间, 是 的开覆盖.
- 对每个 , 由于 同胚于 , 所以 是紧空间.
- 根据引理 3.6.1, 存在 的有限子族 覆盖 .
- 令 , 则 是 中包含 的开集.
- 根据管形引理,存在 中包含 的开集 , 使得 .
- 令 , 则 是 的开覆盖.
- 由 的紧性, 存在 的有限子族 覆盖 .
- 从而, .
- 令 , 则 是 的有限子族且覆盖 . 故 是紧空间.
由定理 3.6.8 和定理 3.6.5, 例 2.6.2 中的环面、Möbius 带、Klein 瓶都是紧空间.
例 3.6.2 【跳过】利用紧性说明正规空间的子空间未必是正规空间
正规空间 的非正规子空间 .
证明
由定理 3.6.1 和定理 3.6.8, 是紧空间. 再由定理 3.6.4, 是正规空间. 下面证明 的子空间 不是正规空间.
令
由于 是 Hausdorff 空间, 则 是 中的闭集 (见习题 3.4.3). 令
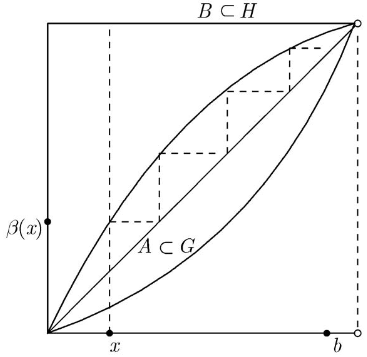
则 与 是 中不相交的非空闭集. 要证 不是正规空间, 只需证如果 和 是 中分别包含 和 的开集, 则 .
假设 . 对任意的 ,有 , 存在 , 使得 . 从而, . 令
则 且 , 见图 3.6.2.
取定 , 定义 . 一般地, 定义 , 则 是 中严格单调增加的序列. 根据推论 1.2.1, 可数集 在 中有上界, 因而有上确界. 记 . 由于 的严格单调增加性, 所以它收敛于 . 于是, 序列 也收敛于 . 因此, 积空间 中的序列 收敛于 . 因为 , 所以当 充分大时, 有 . 这与任意 矛盾. 这表明 .
图 3.6.2