1.2 集合间的基本关系

2024-01-01 22:43:27 新建

我们知道, 两个实数之间有相等关系、大小关系, 如 $5 = 5, 5 < 7, 5 > 3$ , 等等. 两个集合之间是否也有类似的关系呢?

观察

观察下面几个例子, 类比实数之间的相等关系、大小关系, 你能发现下面两个集合之间的关系吗?
(1) $A = {1, 2, 3}, B = {1, 2, 3, 4, 5}$ ;
(2) $C$ 为立德中学高一（2）班全体女生组成的集合, $D$ 为这个班全体学生组成的集合;
(3) $E = {x ∣ x$ 是有两条边相等的三角形 $}, F = {x ∣ x$ 是等腰三角形 $}$ .

可以发现, 在 (1) 中, 集合 $A$ 的任何一个元素都是集合 $B$ 的元素. 这时我们说集合 $A$ 包含于集合 $B$ , 或集合 $B$ 包含集合 $A$ . (2) 中的集合 $C$ 与集合 $D$ 也有这种关系.

定义集合间关系

一般地, 对于两个集合 $A, B$ , 如果集合 $A$ 中任意一个元素都是集合 $B$ 中的元素，就称集合 $A$ 为集合 $B$ 的子集 (subset), 记作 $A \subseteq B$ (或 $B \supseteq A)$ , 读作 “ $A$ 包含于 $B$ ” (或 “ $B$ 包含 $A$ ”).

定义韦恩图

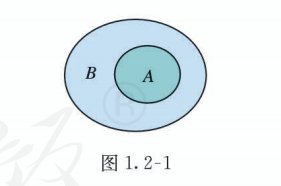
在数学中, 我们经常用平面上封闭曲线的内部代表集合, 这种图称为 Venn 图. 这样, 上述集合 $A$ 与集合 $B$ 的包含关系, 可以用图 1.2-1 表示.

在（3）中，由于 “两条边相等的三角形” 是等腰三角形, 因此, 集合 $E, F$ 都是由所有等腰三角形组成的集合.即集合 $E$ 中任何一个元素都是集合 $F$ 中的元素, 同时, 集合 $F$ 中任何一个元素也都是集合 $E$ 中的元素. 这样, 集合 $E$ 的元素与集合 $F$ 的元素是一样的.

定义

一般地, 如果集合 $A$ 的任何一个元素都是集合 $B$ 的元素, 同时集合 $B$ 的任何一个元素都是集合 $A$ 的元素, 那么集合 $A$ 与集合 $B$ 相等, 记作 $A = B$ .

定理

也就是说, 若 $A \subseteq B$ , 且 $B \subseteq A$ , 则 $A = B$ .

思考

与实数中的结论 “若 $a ⩾ b$ , 且 $b ⩾ a$ , 则 $a = b$ ”相类比, 你有什么体会?

例子

请你举出几个具有包含关系、相等关系的集合实例.

定义

如果集合 $A \subseteq B$ , 但存在元素 $x \in B$ , 且 $x \in / A$ , 就称集合 $A$ 是集合 $B$ 的真子集（proper subset），记作

$A  B (或 B ⫌ A),$

读作 “ $A$ 真包含于 $B$ ” (或 “ $B$ 真包含 $A$ ”).

例子

例如, 在（1）中, $A \subseteq B$ , 但 $4 \in B$ , 且 $4 \in / A$ , 所以集合 $A$ 是集合 $B$ 的真子集.

我们知道, 方程 $x^{2} + 1 = 0$ 没有实数根, 所以方程 $x^{2} + 1 = 0$ 的实数根组成的集合中没有元素.

定义

一般地, 我们把不含任何元素的集合叫做空集 (empty set), 记为 $\emptyset$ , 并规定: 空集是任何集合的子集.

例子

你能举出几个空集的例子吗?

思考

包含关系 ${a} \subseteq A$ 与属于关系 $a \in A$ 有什么区别？试结合实例作出解释.

定理

由上述集合之间的基本关系，可以得到下列结论：
(1) 任何一个集合是它本身的子集, 即

$A \subseteq A;$

(2) 对于集合 $A, B, C$ ，如果 $A \subseteq B$ ，且 $B \subseteq C$ ，那么 $A \subseteq C$ .

例 1

写出集合 ${a, b}$ 的所有子集, 并指出哪些是它的真子集.

解:

集合 ${a, b}$ 的所有子集为 $\emptyset, {a}, {b}, {a, b}$ . 真子集为 $\emptyset, {a}, {b}$ .

例 2

判断下列各题中集合 $A$ 是否为集合 $B$ 的子集, 并说明理由:
(1) $A = {1, 2, 3}, B = {x ∣ x$ 是 8 的约数 $}$ ;
(2) $A = {x ∣ x$ 是长方形 $}, B = {x ∣ x$ 是两条对角线相等的平行四边形 $}$ .

解：

(1) 因为 3 不是 8 的约数, 所以集合 $A$ 不是集合 $B$ 的子集.
(2) 因为若 $x$ 是长方形, 则 $x$ 一定是两条对角线相等的平行四边形, 所以集合 $A$ 是集合 $B$ 的子集.

练习

写出集合 ${a, b, c}$ 的所有子集.

用适当的符号填空:
(1) $a$ ___ ${a, b, c}$ ;
(2) 0 ___ ${x ∣ x^{2} = 0};$
(3) $\emptyset$ ___ ${x \in R ∣ x^{2} + 1 = 0}$ ;
(4) ${0, 1}$ ___ $N$ ;
(5) ${0}$ ___ ${x ∣ x^{2} = x};$
(6) ${2, 1}$ ___ ${x ∣ x^{2} - 3 x + 2 = 0}$ .

判断下列两个集合之间的关系:
(1) $A = {x ∣ x < 0}, B = {x ∣ x < 1}$ ;
(2) $A = {x ∣ x = 3 k, k \in N}, B = {x ∣ x = 6 z, z \in N}$ ;
(3) $A = {x \in N_{+} ∣ x$ 是 4 与 10 的公倍数 $}, B = {x ∣ x = 20 m, m \in N_{+}}$ .

习题 1.2

复习巩固

选用适当的符号填空:
(1) 若集合 $A = {x ∣ 2 x - 3 < 3 x}, B = {x ∣ x ⩾ 2}$ , 则
$- 4$ ___ $B$ , $- 3$ ___ $A$ , ${2}$ ___ $B$ , $B$ ___ $A$ ;
(2) 若集合 $A = {x ∣ x^{2} - 1 = 0}$ , 则
$1$ ___ $A$ , ${- 1}$ ___ $A$ , $\emptyset$ ___ $A$ , ${1, - 1}$ ___ $A$ ;
(3) ${x ∣ x$ 是菱形 $}$ ___ ${x ∣ x$ 是平行四边形 $}$ ;
${x ∣ x$ 是等腰三角形 $}$ ___ ${x ∣ x$ 是等边三角形 $}$ .

指出下列各集合之间的关系, 并用 Venn 图表示:
$A = {x ∣ x$ 是四边形 $}, B = {x ∣ x$ 是平行四边形 $}, C = {x ∣ x$ 是矩形 $}, D = {x ∣ x$ 是正方形 $}$ .

综合运用

举出下列各集合的一个子集:
(1) $A = {x ∣ x$ 是立德中学的学生 $}$ ;
(2) $B = {x ∣ x$ 是三角形 $}$ ;
(3) $C = {0}$ ;
(4) $D = {x \in Z ∣ 3 < x < 30}$ .

在平面直角坐标系中, 集合 $C = {(x, y) ∣ y = x}$ 表示直线 $y = x$ , 从这个角度看, 集合 $D =$ ${(x, y) ∣ {2 x - y = 1 x + 4 y = 5}$ 表示什么? 集合 $C, D$ 之间有什么关系?

拓广探索

(1) 设 $a, b \in R, P = {1, a}, Q = {- 1, - b}$ , 若 $P = Q$ , 求 $a - b$ 的值;
(2) 已知集合 $A = {x ∣ 0 < x < a}, B = {x ∣ 1 < x < 2}$ , 若 $B \subseteq A$ , 求实数 $a$ 的取值范围.