6.2 平面向量的运算
2024-05-17 22:29:10 新建
我们知道, 数能进行运算, 因为有了运算而使数的威力无穷. 那么, 向量是否也能像数一样进行运算呢? 人们从向量的物理背景和数的运算中得到启发, 引进了向量的运算.本节我们就来研究平面向量的运算, 探索其运算性质, 体会向量运算的作用.
下面先学习向量的加法.
6.2.1 向量的加法运算
我们知道, 位移、力是向量, 它们可以合成. 能否从位移、力的合成中得到启发, 引进向量的加法呢?
思考
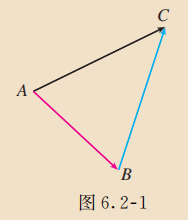
如图 6.2-1, 某质点从点 经过点 到点 , 这个质点的位移如何表示?
答
物理知识告诉我们, 这个质点两次位移 的结果, 与从点 直接到点 的位移 结果相同. 因此, 位移 可以看作位移 与 合成的. 数的加法启发我们, 从运算的角度看, 可以看作 与 的和, 即位移的合成可以看作向量的加法.
如图 6.2-2, 已知非零向量 , 在平面内取任意一点 , 作 , 则向量 叫做 与 的和, 记作 , 即 .

定义 向量加法的三角形法则
求两个向量和的运算, 叫做向量的加法. 这种求向量和的方法, 称为向量加法的三角形法则. 位移的合成可以看作向量加法三角形法则的物理模型.
我们再来看力的合成问题.
思考
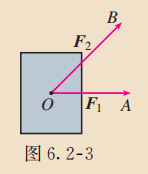
如图 6.2-3, 在光滑的平面上, 一个物体同时受到两个外力 与 的作用, 你能作出这个物体所受的合力 吗?
答
我们知道, 合力 在以 为邻边的平行四边形的对角线上, 并且大小等于这条对角线的长. 从运算的角度看, 可以看作 与 的和, 即力的合成可以看作向量的加法.
定义 向量加法的平行四边形法则
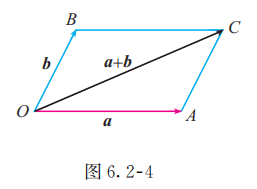
如图 6.2-4, 以同一点 为起点的两个已知向量 , , 以 为邻边作平行四边形 , 则以 为起点的向量 ( 是平行四边形 的对角线) 就是向量 与 的和. 我们把这种作两个向量和的方法叫做向量加法的平行四边形法则. 力的合成可以看作向量加法平行四边形法则的物理模型.
思考
向量加法的平行四边形法则与三角形法则一致吗? 为什么?
定义
对于零向量与任意向量 , 我们规定
例 1
如图 6.2-5, 已知向量 , 求作向量 .
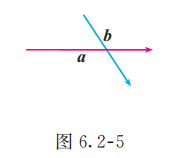
解
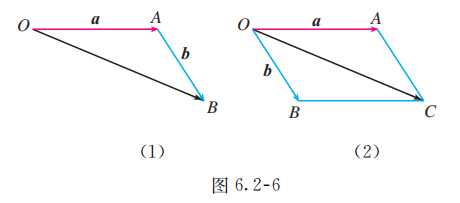
作法 1: 在平面内任取一点 (图 6.2-6 (1) ), 作 . 则 .
作法 2 : 在平面内任取一点 (图 6.2-6 (2) ), 作 . 以 为邻边作平行四边形 , 连接 , 则 .
探究
(1) 如果向量 共线, 它们的加法与数的加法有什么关系? 你能作出向量 吗?
(2) 结合例 1, 探索 之间的关系.
定理
一般地, 我们有
当且仅当 方向相同时等号成立.
根据数的运算的学习经验, 定义了一种运算, 就要研究相应的运算律, 运算律可以有效地简化运算.
探究
数的加法满足交换律、结合律, 向量的加法是否也满足交换律和结合律呢?
定理
向量的加法满足交换律和结合律.
证明
如图 6.2-7 (1), 作 , 以 为邻边作平行四边形 , 容易发现 , 故 . 又 , 所以 .
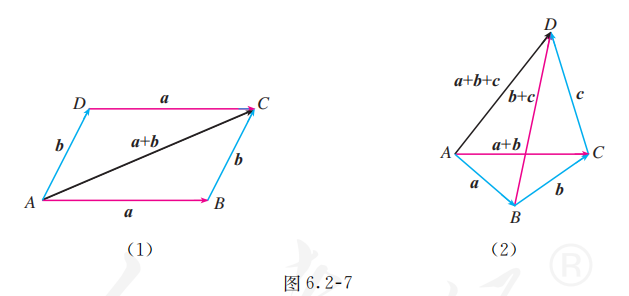
由图 6.2-7 (2), 你能否验证
综上所述, 向量的加法满足交换律和结合律.
例 2
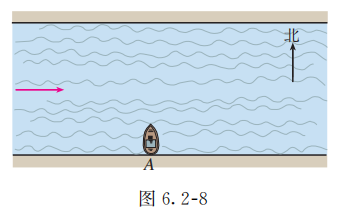
长江两岸之间没有大桥的地方, 常常通过轮渡进行运输. 如图 6.2-8, 一艘船从长江南岸 地出发, 垂直于对岸航行, 航行速度的大小为 , 同时江水的速度为向东 .
(1) 用向量表示江水速度、船速以及船实际航行的速度;
(2) 求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示, 精确到 .
解:
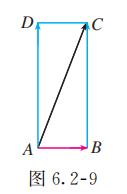
(1) 如图 6.2-9. 表示船速, 表示江水速度,以 , 为邻边作平行四边形 , 则 表示船实际航行的速度.
(2) 在Rt 中, , 于是
因为 , 所以利用计算工具可得 .
因此, 船实际航行速度的大小约为 , 方向与江水速度间的夹角约为 .
练习
1.
如图, 在下列各小题中, 已知向量 , 分别用两种方法求作向量 .
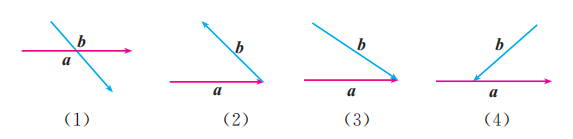
2.
当向量 满足什么条件时, (或 )?
3.
根据图示填空:
(1) ;
(2) ;
(3) ;
(4) .
4.
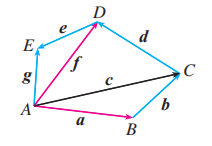
如图, 四边形 是平行四边形, 点 在 上, 判断下列各式是否正确(正确的在括号内打 “ ”, 错误的打 “ ” ).
(1) .
(2) .
(3) .
5.
有一条东西向的小河, 一艘小船从河南岸的渡口出发渡河. 小船航行速度的大小为 , 方向为北偏西 , 河水的速度为向东 , 求小船实际航行速度的大小与方向.
6.2.2 向量的减法运算
思考
在数的运算中, 减法是加法的逆运算, 其运算法则是 “减去一个数等于加上这个数的相反数”. 类比数的减法, 向量的减法与加法有什么关系? 如何定义向量的减法法则?
定义 相反向量
与数 的相反数是 类似, 我们规定, 与向量 长度相等, 方向相反的向量, 叫做 的相反向量, 记作 . 由于方向反转两次仍回到原来的方向, 因此 和 互为相反向量, 于是
我们规定, 零向量的相反向量仍是零向量.
由两个向量和的定义易知
即任意向量与其相反向量的和是零向量. 这样, 如果 互为相反向量, 那么
定义 向量的减法
向量 加上 的相反向量, 叫做 与 的差, 即
求两个向量差的运算叫做向量的减法.
定理
我们看到, 向量的减法可以转化为向量的加法来进行: 减去一个向量相当于加上这个向量的相反向量.
探究
向量减法的几何意义是什么?
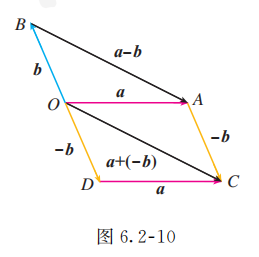
如图 6.2-10, 设 , 连接 ,由向量减法的定义知
在四边形 中, 与 平行且相等, 所以 是平行四边形. 所以
由此, 我们得到 的作图方法.
定理 向量减法的几何意义
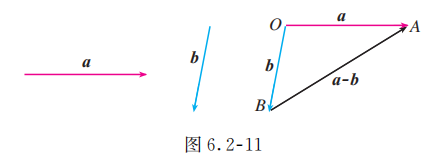
如图 6.2-11, 已知向量 , 在平面内任取一点 , 作 , 则 . 即 可以表示为从向量 的终点指向向量 的终点的向量, 这是向量减法的几何意义.
思考
(1) 在图 6.2-11 中, 如果从 的终点到 的终点作向量, 那么所得向量是什么?
(2) 如果改变图 6.2-11 中向量 的方向, 使 , 怎样作出 呢?
例 3
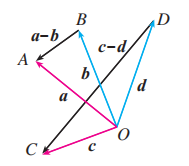
如图, 已知向量 , 求作向量 .
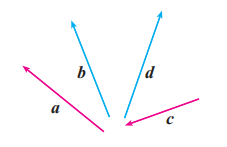
作法:
如图, 在平面内任取一点 , 作 . 则
例 4
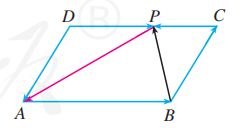
如图 6.2-13, 在平行四边形 中, , 你能用 表示向量 吗?

解:
由向量加法的平行四边形法则, 我们知道
同样, 由向量的减法, 知
练习
1.
如图, 在各小题中, 已知 , 分别求作 .
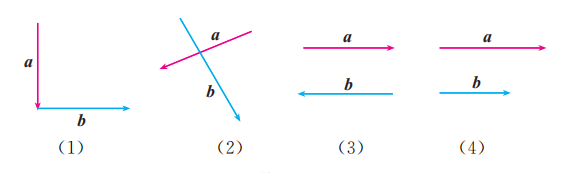
2.
填空:
; ; ;
; .
3.
作图验证: .
6.2.3 向量的数乘运算
探究
已知非零向量 , 作出 和 . 它们的长度和方向分别是怎样的?
如图 6.2-14, . 类比数的乘法, 我们把 记作 , 即 . 显然 的方向与 的方向相同, 的长度是 的长度的 3 倍, 即 .
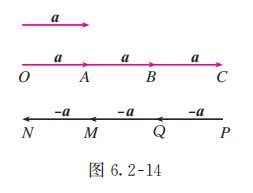
类似地, 由图 6.2-14 可知, , 我们把 记作 , 即 . 显然 的方向与 的方向相反, 的长度是 的长度的 3 倍, 即 .
定义 向量的数乘
一般地, 我们规定实数 与向量 的积是一个向量, 这种运算叫做向量的数乘 (scalar multiplication of vectors), 记作 , 它的长度与方向规定如下:
(1)
(2) 当 时, 的方向与 的方向相同; 当 时, 的方向与 的方向相反.
由 (1) 可知, 当 时, .
你对零向量、相反向量有什么新的认识?
由 (1) (2) 可知, .
思考
你对零向量、相反向量有什么新的认识?
思考
如果把非零向量 的长度伸长到原来的 3.5 倍, 方向不变得到向量 , 向量 该如何表示? 向量 之间的关系怎样?
根据实数与向量的积的定义, 可以验证下面的运算律是成立的.
定理 运算律
设 为实数, 那么
(1)
(2)
(3) .
特别地, 我们有
向量的加、减、数乘运算统称为向量的线性运算. 向量线性运算的结果仍是向量.
对于任意向量 , 以及任意实数 , 恒有
思考
你能证明这些运算律吗?
例 5
计算:
(1) ;
(2) ;
(3) .
解:
(1) 原式 ;
(2) 原式 ;
(3) 原式 .
例 6
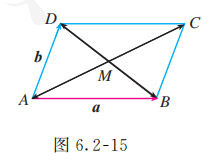
如图 6.2-15, 平行四边形 的两条对角线相交于点 ,且 , 用 表示 和 .
解:
在平行四边形 中,
由平行四边形的两条对角线互相平分, 得
练习
1.
任画一向量 , 分别求作向量 .
2.
点 在线段 上, 且 , 则
3.
把下列各小题中的向量 表示为实数与向量 的积:
(1) ;
(2) ;
(3) ;
(4) .
探究
引入向量数乘运算后, 你能发现实数与向量的积与原向量之间的位置关系吗?
可以发现, 实数与向量的积与原向量共线.
事实上, 对于向量 , 如果有一个实数 , 使 , 那么由向量数乘的定义可知 与 共线.
反过来, 已知向量 与 共线, 且向量 的长度是向量 的长度的 倍, 即 , 那么当 与 同方向时, 有 ; 当 与 反方向时, 有 .
综上, 我们有如下定理:
定理
向量 与 共线的充要条件是:存在唯一一个实数 , 使 .
推论
根据这一定理,设非零向量 位于直线 上,那么对于直线 上的任意一个向量 ,都存在唯一的一个实数 , 使 . 也就是说, 位于同一直线上的向量可以由位于这条直线上的一个非零向量表示.
例 7
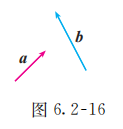
如图 6.2-16, 已知任意两个非零向量 , 试作 . 猜想 三点之间的位置关系, 并证明你的猜想.
分析:
判断三点之间的位置关系, 主要是看这三点是否共线, 为此只要看其中一点是否在另两点所确定的直线上. 在本题中, 应用向量知识判断 三点是否共线, 可以通过判断向量 , 是否共线, 即是否存在 , 使 成立.
解:
分别作向量 , 过点 作直线 (图 6.2-17). 观察发现, 不论向量 怎样变化, 点 始终在直线 上, 猜想 三点共线.
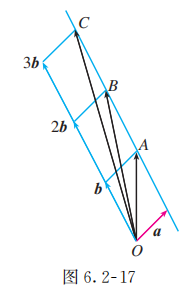
事实上, 因为
所以 .
因此, 三点共线.
例 8
已知 是两个不共线的向量, 向量 共线, 求实数 的值.
解:
由 不共线, 易知向量 为非零向量. 由向量 共线,可知存在实数 , 使得
即
由 不共线, 必有 . 否则, 不妨设 , 则 . 由两个向量共线的充要条件知, 共线, 与已知矛盾.
由 解得 .
因此, 当向量 共线时, .
练习
1.
判断下列各小题中的向量 与 是否共线:
(1) ;
(2) .
2.
化简:
(1) ;
(2) ;
(3) .
3.
已知 是两个不共线的向量, . 若 与 是共线向量, 求实数 的值.
6.2.4 向量的数量积
前面我们学习了向量的加、减运算. 类比数的运算, 出现了一个自然的问题: 向量能否相乘? 如果能, 那么向量的乘法该怎样定义?
在物理课中我们学过功的概念: 如果一个物体在力 的作用下产生位移 (图 6.2-18), 那么力 所做的功
其中 是 与 的夹角.

功是一个标量, 它由力和位移两个向量来确定. 这给我们一种启示, 能否把 “功” 看作两个向量 “相乘” 的结果呢? 受此启发, 我们引入向量 “数量积” 的概念.
因为力做功的计算公式中涉及力与位移的夹角, 所以我们先要定义向量的夹角概念.
定义 向量的夹角
已知两个非零向量 (图 6.2-19), 是平面上的任意一点, 作 , 则 叫做向量 与 的夹角.
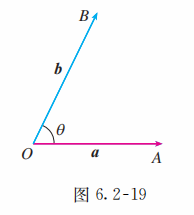
定理
显然, 当 时, 与 同向; 当 时, 与 反向.
如果 与 的夹角是 , 我们说 与 垂直, 记作 .
定义 向量的数量积
已知两个非零向量 与 , 它们的夹角为 , 我们把数量 叫做向量 与 的数量积(或内积(inner product) ), 记作 , 即
的夹角记作 .
规定: 零向量与任一向量的数量积为 0 .
对比向量的线性运算, 我们发现, 向量线性运算的结果是一个向量, 而两个向量的数量积是一个数量, 这个数量的大小与两个向量的长度及其夹角有关.
例 9
已知 与 的夹角 , 求 .
解:
例 10
设 , 求 与 的夹角 .
解:
由 , 得
因为 , 所以 .
定义 投影向量
如图 6.2-20 (1), 设 是两个非零向量, , 我们考虑如下的变换:过 的起点 和终点 , 分别作 所在直线的垂线, 垂足分别为 , 得到 , 我们称上述变换为向量 向向量 投影 (project), 叫做向量 在向量 上的投影向量.

如图 6.2-20 (2), 我们可以在平面内任取一点 , 作 . 过点 作直线 的垂线, 垂足为 , 则 就是向量 在向量 上的投影向量.
探究
如图 6.2-20 (2), 设与 方向相同的单位向量为 与 的夹角为 , 那么 与 之间有怎样的关系?
答
显然, 与 共线, 于是
下面我们探究 与 的关系, 进而给出 的明确表达式. 我们分 为锐角、直角、钝角以及 等情况进行讨论.
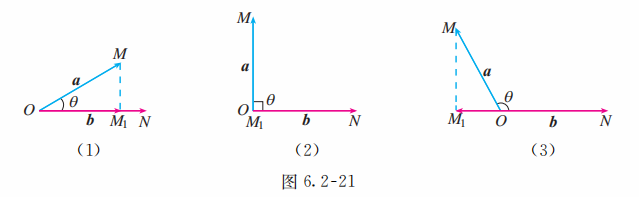
当 为锐角 (图 6.2-21(1))时, 与 方向相同, , 所以
当 为直角 (图 6.2-21(2)) 时, , 所以
当 为钝角 (图 6.2-21(3)) 时, 与 方向相反, 所以
即
当 时, , 所以
当 时, , 所以
从上面的讨论可知, 对于任意的 , 都有
探究
从上面的探究我们看到, 两个非零向量 与 相互平行或垂直时, 向量 在向量 上的投影向量具有特殊性. 这时, 它们的数量积又有怎样的特殊性?
由向量数量积的定义, 可以得到向量数量积的如下重要性质.
定理
设 是非零向量, 它们的夹角是 是与 方向相同的单位向量, 则
(1) .
(2) .
(3) 当 与 同向时, ; 当 与 反向时, . 特别地, 或 .
此外, 由 还可以得到
(4) .
思考
如果 , 是否有 , 或 ?
定义
常常记作 .
练习
1.
已知 和 的夹角是 , 求 .
2.
已知 中, , 当 或 时, 试判断 的形状.
3.
已知 为单位向量, 当向量 的夹角 分别等于 时, 求向量 在向量 上的投影向量.
与向量的线性运算一样, 定义了向量的数量积后, 就要研究数量积运算是否满足一些运算律.
探究
类比数的乘法运算律, 结合向量的线性运算的运算律, 你能得到数量积运算的哪些运算律? 你能证明吗?
由向量数量积的定义, 可以发现下列运算律成立:
定理
对于向量 和实数 , 有
(1) ;
(2) ;
(3) .
证明:
下面我们利用向量投影证明分配律 (3).
如图 6.2-22, 任取一点 , 作 .
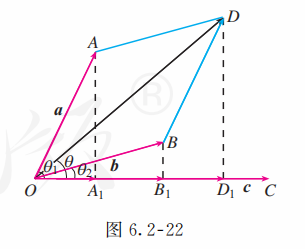
设向量 与 的夹角分别为 , 它们在向量 上的投影向量分别为 , 与 方向相同的单位向量为 , 则
因为 , 所以 . 于是
即
整理, 得
所以
即
所以
因此
思考
设 是向量, 一定成立吗? 为什么?
例 11
我们知道, 对任意 , 恒有
对任意向量 , 是否也有下面类似的结论?
(1) ;
(2) .
解:
(1)
(2)
因此, 上述结论是成立的.
例 12
已知 与 的夹角为 , 求 .
解:
例 13
已知 , 且 与 不共线. 当 为何值时, 向量 与 互相垂直?
解:
与 互相垂直的充要条件是
即
因为 ,
所以 .
解得 .
也就是说, 当 时, 与 互相垂直.
练习
1.
已知 , 向量 与 的夹角为 , 向量 与 的夹角为 , 计算:
(1) ;
(2) .
2.
已知 , 且 与 互相垂直, 求证 .
3.
求证: .
习题 6.2
复习巩固
1.
如果 表示 “向东走 表示 “向西走 ”, 表示 “向北走 表示“向南走 , 那么下列向量具有什么意义?
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) .
2.
一架飞机向北飞行 , 然后改变方向向西飞行 , 求飞机飞行的路程及两次位移的合成.
3.
一艘船垂直于对岸航行, 航行速度的大小为 , 同时河水流速的大小为 . 求船实际航行的速度的大小与方向 (精确到 ).
4.
化简:
(1) ;
(2) ;
(3) ;
(4) ;
(5)
(6) ;
(7) .
5.
作图验证:
(1) ;
(2) .
6.
(1) 已知向量 , 求作向量 , 使 .
(2) (1) 中表示 的有向线段能构成三角形吗?
7.
已知 为两个非零向量,
(1) 求作向量 ;
(2) 当向量 成什么位置关系时, 满足 ? (不要求证明)
8.
化简 :
(1) ;
(2) ;
(3) ;
(4) .
9.
如图, . 求证 .
10.
填空:
(1) 若 满足 , 则 的最大值为 , 最小值为 ;
(2) 当不共线的向量 满足 时, 平分 与 的夹角.
11.
(1) 已知 , 且 与 的夹角 , 求 ;
(2) 已知 , 且 , 求 .
12.
求证:
综合运用
13.
根据下列各小题中的条件, 分别判断四边形 的形状, 并给出证明:
(1) ;
(2) ;
(3) , 且 .
14.
在 中, , 且与边 相交于点 , 的中线 与 相交于点 . 设 , 用 分别表示向量 .
15.
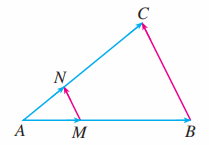
如图, 在任意四边形 中, 分别为 的中点, 求证: .
16.
飞机从甲地沿北偏西 的方向飞行 到达乙地, 再从乙地沿南偏东 的方向飞行 到达丙地. 画出飞机飞行的位移示意图, 并说明丙地在甲地的什么方向? 丙地距甲地多远?
17.
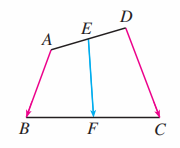
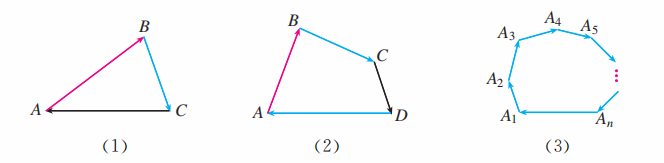
(1) 如图 (1), 在 中, 计算 ;
(2) 如图 (2), 在四边形 中, 计算 ;
(3) 如图 (3), 在 边形 中, ? 证明你的结论.
18.
已知 , 且 , 求 与 的夹角 .
19.
已知 , 且 , 求 与 的夹角 (精确到 ). (可用计算工具)
20.
已知 是非零向量, , 求证:
拓广探索
21.
已知 的外接圆圆心为 , 且 , 则向量 在向量 上的投影向量为 .
(A)
(B)
(C)
(D)
22.
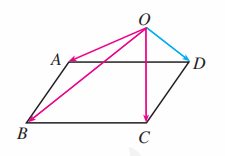
如图, 是平行四边形 外一点, 用 表示 .
23.
已知 为四边形 所在平面内一点, 且向量 满足等式
(1) 作出满足条件的四边形 .
(2) 四边形 有什么特点? 请证明你的猜想.
24.
如图, 在 中, 是不是只需知道 的半径或弦 的长度, 就可以求出 的值?