7.2 复数的四则运算
2024-06-16 22:26:56 新建
在上一节, 我们把实数集扩充到了复数集. 引入新数集后, 就要研究其中的数之间的运算. 下面就来讨论复数集中的运算问题.
7.2.1 复数的加、减运算及其几何意义
我们规定, 复数的加法法则如下:
设 是任意两个复数, 那么它们的和
很明显, 两个复数的和仍然是一个确定的复数. 特别地, 当 都是实数时, 把它们看作复数时的和就是这两个实数的和.
可以看出, 两个复数相加, 类似于两个多项式相加.
思考
复数的加法满足交换律、结合律吗?
定理
容易得到, 对任意 , 有
探究
我们知道, 复数与复平面内以原点为起点的向量一一对应. 而我们讨论过向量加法的几何意义, 你能由此出发讨论复数加法的几何意义吗?
定理 复数加法的几何意义
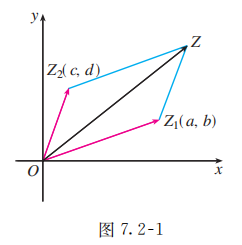
设 分别与复数 对应, 则 . 由平面向量的坐标运算法则, 得
这说明两个向量 与 的和就是与复数 对应的向量. 因此, 复数的加法可以按照向量的加法来进行 (图 7.2-1), 这就是复数加法的几何意义.
思考
我们知道, 实数的减法是加法的逆运算. 类比实数减法的意义, 你认为该如何定义复数的减法?
定理 复数的减法法则
我们规定, 复数的减法是加法的逆运算, 即把满足
的复数 叫做复数 减去复数 的差, 记作
根据复数相等的含义,
因此
所以
即
这就是复数的减法法则. 由此可见, 两个复数的差是一个确定的复数. 可以看出, 两个复数相减, 类似于两个多项式相减.
探究
类比复数加法的几何意义, 你能得出复数减法的几何意义吗?
例 1
计算 .
解:
例 2
根据复数及其运算的几何意义, 求复平面内的两点 之间的距离.
分析:
由于复平面内的点 对应的复数分别为 , 由复数减法的几何意义知, 复数 对应的向量为 , 从而点 之间的距离为 .
解:
因为复平面内的点 对应的复数分别为 , , 所以点 之间的距离为
练习
1.
计算:
(1) ;
(2) ;
(3) ;
(4) .
2.
如图, 向量 对应的复数是 , 分别作出下列运算的结果对应的向量:
(1) ;
(2) ;
(3) .
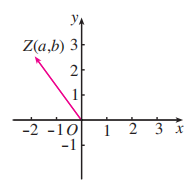
3.
证明复数的加法满足交换律、结合律.
4.
求复平面内下列两个复数对应的两点之间的距离:
(1) ;
(2) .
7.2.2 复数的乘、除运算
定义
我们规定, 复数的乘法法则如下:
设 是任意两个复数, 那么它们的积
很明显, 两个复数的积是一个确定的复数. 特别地, 当 都是实数时, 把它们看作复数时的积就是这两个实数的积.
可以看出, 两个复数相乘, 类似于两个多项式相乘, 只要在所得的结果中把 换成 , 并且把实部与虚部分别合并即可.
思考
复数的乘法是否满足交换律、结合律? 乘法对加法满足分配律吗?
定理
容易得到, 对于任意 , 有
例 3
计算 .
解:
例 4
计算:
(1) ;
(2) .
分析:
本例可以用复数的乘法法则计算, 也可以用乘法公式计算.
这里 “乘法公式” 指的是与实数系中的乘法公式相对应的公式.
解:
(1)
(2)
思考
若 是共轭复数, 则 是一个怎样的数?
探究
类比实数的除法是乘法的逆运算, 我们规定复数的除法是乘法的逆运算. 请探求复数除法的法则.
定义
复数除法的法则是:
由此可见, 两个复数相除 (除数不为 0 ), 所得的商是一个确定的复数.
在进行复数除法运算时, 通常先把 写成 的形式, 再把分子与分母都乘分母的共轴复数 , 化简后就可得到上面的结果. 这里分子分母都乘分母的 “实数化因式” (共轭复数), 从而使分母 “实数化”.
例 5
计算 .
解:
例 6
在复数范围内解下列方程:
(1) ;
(2) , 其中 , 且 .
分析:
利用复数的乘法容易得到 (1) 中方程的根. 对于 (2), 当 时, 一元二次方程 无实数根. 利用求解一元二次方程的 “根本大法” —— 配方法, 类似于 (1), 就能在复数范围内求得 (2) 中方程的根.
解:
(1) 因为 , 所以方程 的根为 .
(2) 将方程 的二次项系数化为 1 , 得
配方, 得
即
由 , 知 . 类似 (1), 可得
所以原方程的根为 .
定理
在复数范围内, 实系数一元二次方程 的求根公式为:
(1) 当 时, ;
(2) 当 时, .
思考
根据复数的加法法则、乘法法则, 你能说明实数系经过扩充后得到的新数集就是复数集 吗?
练习
1.
计算:
(1) ;
(2) ;
(3) .
2.
计算:
(1) ;
(2) ;
(3) .
3.
计算:
(1) ;
(2) ;
(3) ;
(4) .
4.
在复数范围内解下列方程:
(1) ;
(2) .
习题 7.2
复习巩固
1.
计算:
(1) ;
(2) ;
(3) ;
(4) .
2.
在复平面内, 复数 对应的向量分别是 , 其中 是原点, 求向量 , 对应的复数.
3.
计算:
(1) ;
(2) ;
(3) ;
(4) ;
(5) .
4.
计算:
(1) ;
(2) ;
(3) ;
(4) .
综合运用
5.
四边形 是复平面内的平行四边形, 三点对应的复数分别是 ,求点 对应的复数.
6.
在复数范围内解下列方程:
(1) ;
(2) .
7.
已知 是关于 的方程 的一个根, 求实数 的值.
拓广探索
8.
利用公式 , 把下列各式分解成一次因式的积:
(1) ;
(2) .
9.
若 , 则复平面内满足 的点 的集合是什么图形?
10.
使用信息技术手段进行试验:尝试在复数集中对实系数多项式进行因式分解, 观察并记录所发现的规律.
阅读与思考
代数基本定理
在代数发展史上的很长一段时期内, 解一元多项式方程一直是人们研究的一个中心问题. 早在古巴比伦时期, 人们就会解一元二次方程. 16 世纪上半叶, 数学家们得到了一元三次方程、一元四次方程的解法 (包括求根公式). 此后, 数学家们转向求解一元五次及五次以上的方程. 他们想弄清楚以下问题: 一般的一元多项式方程有没有根? 如果有根, 根的个数是多少? 是否存在求根公式?
我们可以发现这样一个现象: 随机生成的一元多项式, 在复数集中最终都可以分解成一次因式的乘积, 且一次因式的个数(包括重复因式)就是被分解的多项式的次数. 事实上, 数学中有如下定理:
定理
代数基本定理(fundamental theorem of algebra) 任何一元 次复系数多项式方程 至少有一个复数根.
代数基本定理是数学中最重要的定理之一, 它在代数学中起着基础作用. 代数基本定理的证明方法有很多种, 但每种证法都涉及高等数学知识, 此处不作介绍. 有兴趣的同学可以查阅相关资料.
由代数基本定理可以得到:任何一元 次复系数多项式 在复数集中可以分解为 个一次因式的乘积. 进而, 一元 次多项式方程有 个复数根(重根按重数计). 你能给出证明吗?
尽管一元 次多项式方程有 个复数根(重根按重数计), 但是一元五次及五次以上的方程不存在一般的求根公式.
下面我们从代数基本定理出发,看看一元多项式方程的根与系数之间的关系.
设实系数一元二次方程
在复数集 内的根为 , 容易得到
设实系数一元三次方程
在复数集 内的根为 , 可以得到, 方程 (1) 可变形为
展开得
比较 (1) (2) 可以得到
思考
如果实系数一元四次方程
在复数集 内的根为 , 那么它们与方程的系数之间有什么关系呢?
思考
对于上述方程, 如果系数是复数, 那么根与系数的这些关系仍然成立吗?