5.5 三角恒等变换

2024-04-16 22:38:49 新建

前面我们学习了诱导公式, 利用它们对三角函数式进行恒等变形, 可以达到化简、求值或证明的目的. 这种利用公式对三角函数式进行的恒等变形就是三角恒等变换. 观察诱导公式, 可以发现它们都是特殊角与任意角 $α$ 的和（或差）的三角函数与这个任意角 $α$ 的三角函数的恒等关系. 如果把特殊角换为任意角 $β$ , 那么任意角 $α$ 与 $β$ 的和（或差）的三角函数与 $α, β$ 的三角函数会有什么关系呢? 下面来研究这个问题.

5.5.1 两角和与差的正弦、余弦和正切公式

1. 两角差的余弦公式

探究

如果已知任意角 $α, β$ 的正弦、余弦, 能由此推出 $α + β, α - β$ 的正弦、余弦吗?

[补] 引理圆的旋转对称性

任意一个圆绕着其圆心旋转任意角后都与原来的圆重合, 这一性质叫做圆的旋转对称性.

[补] 引理平面上任意两点间的距离公式

平面上任意两点 $P_{1} (x_{1}, y_{1}), P_{2} (x_{2}, y_{2})$ 间的距离公式 $P_{1} P_{2} = (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}$ .

下面, 我们来探究 $cos (α - β)$ 与角 $α, β$ 的正弦、余弦之间的关系.

不妨令 $α \neq = 2 kπ + β, k \in Z$ .

如图 5.5-1, 设单位圆与 $x$ 轴的正半轴相交于点 $A (1, 0)$ , 以 $x$ 轴非负半轴为始边作角 $α, β, α - β$ ,它们的终边分别与单位圆相交于点 $P_{1} (cos α, sin α)$ , $A_{1} (cos β, sin β), P (cos (α - β), sin (α - β))$ .

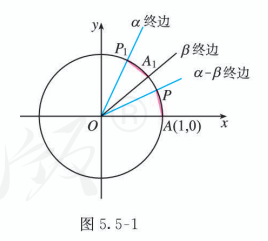
连接 $A_{1} P_{1}, A P$ . 若把扇形 $O A P$ 绕着点 $O$ 旋转 $β$ 角, 则点 $A, P$ 分别与点 $A_{1}, P_{1}$ 重合. 根据圆的旋转对称性可知, $A P$ 与 $A_{1} P_{1}$ 重合, 从而 $A P = A_{1} P_{1}$ ,所以 $A P = A_{1} P_{1}$ .

根据两点间的距离公式, 得

$= [cos (α - β) - 1]^{2} + sin^{2} (α - β) (cos α - cos β)^{2} + (sin α - sin β)^{2},$

化简得

$cos (α - β) = cos α cos β + sin α sin β .$

当 $α = 2 kπ + β (k \in Z)$ 时, 容易证明上式仍然成立.

定理差角的余弦公式

所以, 对于任意角 $α, β$ 有

$cos (α - β) = cos α cos β + sin α sin β . (C_{(α - β)})$

此公式给出了任意角 $α, β$ 的正弦、余弦与其差角 $α - β$ 的余弦之间的关系, 称为差角的余弦公式，简记作 $C_{(α - β)}$ .

例 1

利用公式 $C_{(α - β)}$ 证明：
(1) $cos (\frac{π}{2} - α) = sin α$ ;
(2) $cos (π - α) = - cos α$ .

证明:

(1)

$cos (\frac{π}{2} - α) = cos \frac{π}{2} cos α + sin \frac{π}{2} sin α = 0 + 1 \times sin α = sin α .$

(2)

$cos (π - α) = cos π cos α + sin π sin α = (- 1) \times cos α + 0 = - cos α$

例 2

已知 $sin α = \frac{4}{5}, α \in (\frac{π}{2}, π), cos β = - \frac{5}{13}, β$ 是第三象限角, 求 $cos (α - β)$ 的值.

解:

由 $sin α = \frac{4}{5}, α \in (\frac{π}{2}, π)$ , 得

$cos α = - 1 - sin^{2} α = - 1 - (\frac{4}{5})^{2} = - \frac{3}{5} .$

又由 $cos β = - \frac{5}{13}, β$ 是第三象限角, 得

$sin β = - 1 - cos^{2} β = - 1 - (- \frac{5}{13})^{2} = - \frac{12}{13} .$

所以

$cos (α - β) = cos α cos β + sin α sin β = (- \frac{3}{5}) \times (- \frac{5}{13}) + \frac{4}{5} \times (- \frac{12}{13}) = - \frac{33}{65} .$

练习

利用公式 $C_{(α - β)}$ 证明:
(1) $cos (\frac{3 π}{2} - α) = - sin α$ ;
(2) $cos (- α) = cos α$ .

利用公式 $C_{(α - β)}$ 求 $cos 1 5^{\circ}$ 的值.

已知 $cos α = - \frac{3}{5}, α \in (\frac{π}{2}, π)$ , 求 $cos (\frac{π}{4} - α)$ 的值.

已知 $sin θ = \frac{15}{17}, θ$ 是第二象限角, 求 $cos (θ - \frac{π}{3})$ 的值.

已知 $sin α = - \frac{2}{3}, α \in (π, \frac{3 π}{2}), cos β = \frac{3}{4}, β \in (\frac{3 π}{2}, 2 π)$ , 求 $cos (β - α)$ 的值.

2. 两角和与差的正弦、余弦、正切公式

思考

由公式 $C_{(α - β)}$ 出发, 你能推导出两角和与差的三角函数的其他公式吗?

下面以公式 $C_{(α - β)}$ 为基础来推导其他公式.

例如, 比较 $cos (α - β)$ 与 $cos (α + β)$ , 并注意到 $α + β$ 与 $α - β$ 之间的联系: $α + β = α - (- β)$ , 则由公式 $C_{(α - β)}$ , 有

$cos (α + β) = cos [α - (- β)] = cos α cos (- β) + sin α sin (- β) = cos α cos β - sin α sin β .$

定理两角和的余弦公式

于是得到了两角和的余弦公式, 简记作 $C_{(α + β)}$ .

$cos (α + β) = cos α cos β - sin α sin β . (C_{(α + β)})$

证法 2

这里用到的是加法和减法的联系, 也可用换元的观点来考虑: 由于公式 $C_{(α - β)}$ 对于任意 $α, β$ 都成立, 那么把其中的 $β$ 换成 - $β$ 后, 也一定成立. 由此也可推得公式 $C_{(α + β)}$ .

探究

上面得到了两角和与差的余弦公式. 我们知道, 用诱导公式五（或六）可以实现正弦、余弦的互化. 你能根据 $C_{(α + β)}, C_{(α - β)}$ 及诱导公式五 (或六), 推导出用任意角 $α, β$ 的正弦、余弦表示 $sin (α + β), sin (α - β)$ 的公式吗?

定理

通过推导, 可以得到:

$sin (α + β) = sin α cos β + cos α sin β, (S_{(α + β)}) sin (α - β) = sin α cos β - cos α sin β . (S_{(α - β)})$

探究

你能根据正切函数与正弦函数、余弦函数的关系, 从 $C_{(α \pm β)}, S_{(α \pm β)}$ 出发, 推导出用任意角 $α, β$ 的正切表示 $tan (α + β), tan (α - β)$ 的公式吗?

定理

通过推导, 可以得到:

$tan (α + β) = \frac{tan α + tan β}{1 - tan α tan β}, (T_{(α + β)}) tan (α - β) = \frac{tan α - tan β}{1 + tan α tan β} . (T_{(α - β)})$

定义和角公式，差角公式

公式 $S_{(α + β)}, C_{(α + β)}, T_{(α + β)}$ 给出了任意角 $α, β$ 的三角函数值与其和角 $α + β$ 的三角函数值之间的关系. 为方便起见, 我们把这三个公式都叫做和角公式.

类似地, $S_{(α - β)}, C_{(α - β)}, T_{(α - β)}$ 都叫做差角公式.

探究

和 (差) 角公式中, $α, β$ 都是任意角. 如果令 $α$ 为某些特殊角, 就能得到许多有用的公式. 你能从和 (差) 角公式出发推导出诱导公式吗? 你还能得到哪些等式?

例 3

已知 $sin α = - \frac{3}{5}$ ， $α$ 是第四象限角, 求 $sin (\frac{π}{4} - α), cos (\frac{π}{4} + α), tan (α - \frac{π}{4})$ 的值.

解:

由 $sin α = - \frac{3}{5}$ ， $α$ 是第四象限角, 得

$cos α = 1 - sin^{2} α = 1 - (- \frac{3}{5})^{2} = \frac{4}{5},$

所以

$tan α = \frac{sin α}{cos α} = \frac{- \frac{3}{5}}{\frac{4}{5}} = - \frac{3}{4} .$

于是有

$sin (\frac{π}{4} - α) = sin \frac{π}{4} cos α - cos \frac{π}{4} sin α = \frac{2}{2} \times \frac{4}{5} - \frac{2}{2} \times (- \frac{3}{5}) = \frac{7 2}{10};$

$cos (\frac{π}{4} + α) = cos \frac{π}{4} cos α - sin \frac{π}{4} sin α = \frac{2}{2} \times \frac{4}{5} - \frac{2}{2} \times (- \frac{3}{5}) = \frac{7 2}{10};$

$tan (α - \frac{π}{4}) = \frac{tan α - tan \frac{π}{4}}{1 + tan α tan \frac{π}{4}} = \frac{tan α - 1}{1 + tan α} = \frac{- \frac{3}{4} - 1}{1 + ( - \frac{3}{4} )} = - 7.$

思考

由以上解答可以看到, 在本题条件下有 $sin (\frac{π}{4} - α) = cos (\frac{π}{4} + α)$ . 那么对于任意角 $α$ , 此等式成立吗? 若成立, 你会用几种方法予以证明?

例 4

利用和 (差) 角公式计算下列各式的值:
(1) $sin 7 2^{\circ} cos 4 2^{\circ} - cos 7 2^{\circ} sin 4 2^{\circ}$ ;
(2) $cos 2 0^{\circ} cos 7 0^{\circ} - sin 2 0^{\circ} sin 7 0^{\circ}$ ;
(3) $\frac{1 + tan 1 5 ^{\circ}}{1 - tan 1 5 ^{\circ}}$ .

分析:

和、差角公式把 $α \pm β$ 的三角函数式转化成了 $α, β$ 的三角函数式. 如果反过来, 从右到左使用公式, 就可以将上述三角函数式化简.

解:

(1) 由公式 $S_{(α - β)}$ , 得

$= = = sin 7 2^{\circ} cos 4 2^{\circ} - cos 7 2^{\circ} sin 4 2^{\circ} sin (7 2^{\circ} - 4 2^{\circ}) sin 3 0^{\circ} \frac{1}{2} .$

(2) 由公式 $C_{(a + β)}$ , 得

$= = = cos 2 0^{\circ} cos 7 0^{\circ} - sin 2 0^{\circ} sin 7 0^{\circ} cos (2 0^{\circ} + 7 0^{\circ}) cos 9 0^{\circ} 0.$

(3) 由公式 $T_{(α + β)}$ 及 $tan 4 5^{\circ} = 1$ , 得

$\frac{1 + tan 1 5 ^{\circ}}{1 - tan 1 5 ^{\circ}} = \frac{tan 4 5 ^{\circ} + tan 1 5 ^{\circ}}{1 - tan 4 5 ^{\circ} tan 1 5 ^{\circ}} = tan (4 5^{\circ} + 1 5^{\circ}) = tan 6 0^{\circ} = 3 .$

练习

利用和 (差) 角公式, 求下列各式的值:
(1) $sin 1 5^{\circ}$ ;
(2) $cos 7 5^{\circ}$ ;
(3) $sin 7 5^{\circ}$ ;
(4) $tan 1 5^{\circ}$ .

(1) 已知 $cos θ = - \frac{3}{5}, θ \in (\frac{π}{2}, π)$ , 求 $sin (θ + \frac{π}{3})$ 的值;
(2) 已知 $sin θ = - \frac{12}{13}, θ$ 是第三象限角, 求 $cos (\frac{π}{6} + θ)$ 的值;
(3) 已知 $tan α = 3$ , 求 $tan (α + \frac{π}{4})$ 的值.

求下列各式的值:
(1) $sin 7 2^{\circ} cos 1 8^{\circ} + cos 7 2^{\circ} sin 1 8^{\circ}$ ;
(2) $cos 7 2^{\circ} cos 1 2^{\circ} + sin 7 2^{\circ} sin 1 2^{\circ}$ ;
(3) $\frac{tan 1 2 ^{\circ} + tan 3 3 ^{\circ}}{1 - tan 1 2 ^{\circ} tan 3 3 ^{\circ}}$ ;
(4) $cos 7 4^{\circ} sin 1 4^{\circ} - sin 7 4^{\circ} cos 1 4^{\circ}$ ;
(5) $sin 3 4^{\circ} sin 2 6^{\circ} - cos 3 4^{\circ} cos 2 6^{\circ}$ ;
(6) $sin 2 0^{\circ} cos 11 0^{\circ} + cos 16 0^{\circ} sin 7 0^{\circ}$ .

化简:
(1) $\frac{1}{2} cos x - \frac{3}{2} sin x$ ;
(2) $3 sin x + cos x$ ;
(3) $2 (sin x - cos x)$ ;
(4) $2 cos x - 6 sin x$ .

已知 $sin (α - β) cos α - cos (β - α) sin α = \frac{3}{5}, β$ 是第三象限角, 求 $sin (β + \frac{5 π}{4})$ 的值.

3. 二倍角的正弦、余弦、正切公式

以公式 $C_{(α - β)}$ 为基础, 我们已经得到六个和（差）角公式, 下面将以和（差）角公式为基础来推导倍角公式.

探究

你能利用 $S_{(α \pm β)}, C_{(α \pm β)}, T_{(α \pm β)}$ 推导出 $sin 2 α, cos 2 α, tan 2 α$ 的公式吗?

定理倍角公式

通过推导, 可以得到:

$sin 2 α cos 2 α tan 2 α = 2 sin α cos α, = cos^{2} α - sin^{2} α, = \frac{2 tan α}{1 - tan ^{2} α} . (S_{2 α}) (C_{2 α}) (T_{2 α})$

如果要求二倍角的余弦公式 $(C_{2 α})$ 中仅含 $α$ 的正弦 (余弦), 那么又可得到:

$cos 2 α = 1 - 2 sin^{2} α, cos 2 α = 2 cos^{2} α - 1.$

以上这些公式都叫做倍角公式. 倍角公式给出了 $α$ 的三角函数与 $2 α$ 的三角函数之间的关系.

这里的“倍角” 专指 “二倍角”, 遇到“三倍角”等名词时, “三”字等不可省去.

归纳

从和 (差) 角公式、倍角公式的推导过程可以发现, 这些公式存在紧密的逻辑联系, 请你进行归纳总结.

例 5

已知 $sin 2 α = \frac{5}{13}, \frac{π}{4} < α < \frac{π}{2}$ , 求 $sin 4 α, cos 4 α, tan 4 α$ 的值.

分析：

已知条件给出了 $2 α$ 的正弦函数值. 由于 $4 α$ 是 $2 α$ 的二倍角, 因此可以考虑用倍角公式.

解:

由 $\frac{π}{4} < α < \frac{π}{2}$ , 得

$\frac{π}{2} < 2 α < π .$

又

$sin 2 α = \frac{5}{13},$

所以

$cos 2 α = - 1 - (\frac{5}{13})^{2} = - \frac{12}{13} .$

于是

$sin 4 α cos 4 α tan 4 α = sin [2 \times (2 α)] = 2 sin 2 α cos 2 α = 2 \times \frac{5}{13} \times (- \frac{12}{13}) = - \frac{120}{169}; = cos [2 \times (2 α)] = 1 - 2 sin^{2} 2 α = 1 - 2 \times (\frac{5}{13})^{2} = \frac{119}{169}; = \frac{sin 4 α}{cos 4 α} = - \frac{120}{169} \times \frac{169}{119} = - \frac{120}{119} .$

“倍” 是描述两个数量之间关系的, $2 α$ 是 $α$ 的二倍, $4 α$ 是 $2 α$ 的二倍, $\frac{α}{2}$ 是 $\frac{α}{4}$ 的二倍, 这里蕴含着换元思想.

例 6

在 $△ A BC$ 中, $cos A = \frac{4}{5}, tan B = 2$ , 求 $tan (2 A + 2 B)$ 的值.

思考

$2 A + 2 B$ 与 $A, B$ 之间能构成怎样的关系?

解法 1:

在 $△ A BC$ 中,

由 $cos A = \frac{4}{5}, 0 < A < π$ , 得

$sin A = 1 - cos^{2} A = 1 - (\frac{4}{5})^{2} = \frac{3}{5},$

所以

$tan A tan 2 A = \frac{sin A}{cos A} = \frac{3}{5} \times \frac{5}{4} = \frac{3}{4}, = \frac{2 tan A}{1 - tan ^{2} A} = \frac{2 \times \frac{3}{4}}{1 - ( \frac{3}{4} ) ^{2}} = \frac{24}{7} .$

又

$tan B = 2,$

所以

$tan 2 B = \frac{2 tan B}{1 - tan ^{2} B} = \frac{2 \times 2}{1 - 2 ^{2}} = - \frac{4}{3} .$

于是

$tan (2 A + 2 B) = \frac{tan 2 A + tan 2 B}{1 - tan 2 A tan 2 B} = \frac{\frac{24}{7} - \frac{4}{3}}{1 - \frac{24}{7} \times ( - \frac{4}{3} )} = \frac{44}{117} .$

解法 2:

在 $△ A BC$ 中,

由 $cos A = \frac{4}{5}, 0 < A < π$ , 得

$sin A = 1 - cos^{2} A = 1 - (\frac{4}{5})^{2} = \frac{3}{5},$

所以

$tan A = \frac{sin A}{cos A} = \frac{3}{5} \times \frac{5}{4} = \frac{3}{4} .$

又

$tan B = 2,$

所以

$tan (A + B) = \frac{tan A + tan B}{1 - tan A tan B} = \frac{\frac{3}{4} + 2}{1 - \frac{3}{4} \times 2} = - \frac{11}{2},$

所以

$tan (2 A + 2 B) = tan [2 (A + B)] = \frac{2 tan ( A + B )}{1 - tan ^{2} ( A + B )} = \frac{2 \times ( - \frac{11}{2} )}{1 - ( - \frac{11}{2} ) ^{2}} = \frac{44}{117} .$

练习

已知 $cos \frac{α}{8} = - \frac{4}{5}, 8 π < α < 12 π$ , 求 $sin \frac{α}{4}, cos \frac{α}{4}, tan \frac{α}{4}$ 的值.

已知 $sin (α - π) = \frac{3}{5}$ , 求 $cos 2 α$ 的值.

已知 $sin 2 α = - sin α, α \in (\frac{π}{2}, π)$ , 求 $tan α$ 的值.

已知 $tan 2 α = \frac{1}{3}$ , 求 $tan α$ 的值.

求下列各式的值:
(1) $sin 1 5^{\circ} cos 1 5^{\circ}$ ;
(2) $cos^{2} \frac{π}{8} - sin^{2} \frac{π}{8}$ ;
(3) $\frac{tan 22. 5 ^{\circ}}{1 - tan ^{2} 22. 5 ^{\circ}}$ ;
(4) $2 cos^{2} 22. 5^{\circ} - 1$ .

信息技术应用

利用信息技术制作三角函数表

前面在 “对数的发明” 中曾经谈到, 纳皮尔利用对数制作了 $0^{\circ} \sim 9 0^{\circ}$ 每隔 $1^{'}$ 的八位三角函数表. 应当说, 纳皮尔仅仅凭借手工运算得到这个三角函数表的工作量是非常大的, 这也显示出他超人的效力和为科学献身的精神. 今天, 我们可以利用已经学会的三角函数知识以及算法知识, 借助信息技术, 容易地制作出非常精确的三角函数表. 下面我们借助信息技术来作一个 $0^{\circ} \sim 9 0^{\circ}$ 每隔 $1^{'}$ 的八位三角函数表.

用计算工具可得:

$sin 1^{'} \approx 2.908882046 \times 1 0^{- 4} \approx 0.000290888.$

以此作为初始值, 利用

$cos 1^{'} = 1 - sin^{2} 1^{'}; α_{0} = 1^{'}, α_{n} = α_{n - 1} + 1^{'}, n ⩾ 1; sin α_{n} = sin 1^{'} cos α_{n - 1} + cos 1^{'} sin α_{n - 1}, cos α_{n} = 1 - sin^{2} α_{n},$

就可以写出一个程序框图 (如右图所示), 然后通过信息技术得到一个正弦函数的三角函数表.

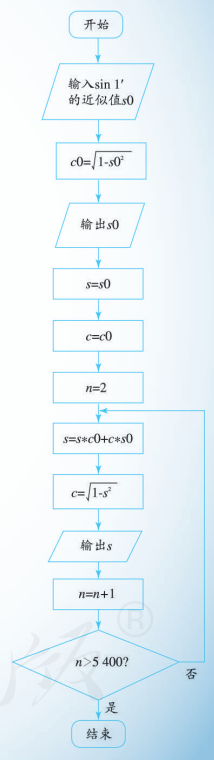
请同学们根据上述思路, 自己编写程序, 得出一个三角函数表.

5.5.2 简单的三角恒等变换

学习了和 (差) 角公式、二倍角公式以后, 我们就有了进行三角恒等变换的新工具,从而使三角恒等变换的内容、思路和方法更加丰富.

例 7

试以 $cos α$ 表示 $sin^{2} \frac{α}{2}, cos^{2} \frac{α}{2}, tan^{2} \frac{α}{2}$ .

思考

$α$ 与 $\frac{α}{2}$ 有什么关系?

解:

$α$ 是 $\frac{α}{2}$ 的二倍角. 在倍角公式 $cos 2 α = 1 - 2 sin^{2} α$ 中, 以 $α$ 代替 $2 α$ , 以 $\frac{α}{2}$ 代替 $α$ , 得

$cos α = 1 - 2 sin^{2} \frac{α}{2},$

所以

$sin^{2} \frac{α}{2} = \frac{1 - cos α}{2} . (\overset{◯}{1})$

在倍角公式 $cos 2 α = 2 cos^{2} α - 1$ 中, 以 $α$ 代替 $2 α$ , 以 $\frac{α}{2}$ 代替 $α$ , 得

$cos α = 2 cos^{2} \frac{α}{2} - 1,$

所以

$cos^{2} \frac{α}{2} = \frac{1 + cos α}{2} . (\overset{◯}{2})$

将 $\overset{◯}{1}$ $\overset{◯}{2}$ 两个等式的左右两边分别相除, 得

$tan^{2} \frac{α}{2} = \frac{1 - cos α}{1 + cos α} .$

定理半角公式

例 7 的结果还可以表示为:

$sin \frac{α}{2} = \pm \frac{1 - cos α}{2}, cos \frac{α}{2} = \pm \frac{1 + cos α}{2}, tan \frac{α}{2} = \pm \frac{1 - cos α}{1 + cos α},$

并称之为半角公式, 符号由 $\frac{α}{2}$ 所在象限决定。

因为不同的三角函数式不仅会有结构形式方面的差异, 而且还会存在所包含的角, 以及这些角的三角函数种类方面的差异, 所以进行三角恒等变换时, 常常要先寻找式子所包含的各个角之间的联系, 并以此为依据选择适当的公式. 这是三角恒等变换的一个重要特点.

例 8

求证:
(1) $sin α cos β = \frac{1}{2} [sin (α + β) + sin (α - β)]$ ;
(2) $sin θ + sin φ = 2 sin \frac{θ + φ}{2} cos \frac{θ - φ}{2}$ .

思考

这两个式子的左右两边在结构形式上有什么不同?

证明：

(1) 因为

$sin (α + β) = sin α cos β + cos α sin β, sin (α - β) = sin α cos β - cos α sin β,$

将以上两式的左右两边分别相加, 得

$sin (α + β) + sin (α - β) = 2 sin α cos β,$

即

$sin α cos β = \frac{1}{2} [sin (α + β) + sin (α - β)] .$

(2) 由 (1) 可得

$sin (α + β) + sin (α - β) = 2 sin α cos β . (\overset{◯}{1})$

设 $α + β = θ, α - β = φ$ ,那么

$α = \frac{θ + φ}{2}, β = \frac{θ - φ}{2} .$

把 $α, β$ 的值代入 $\overset{◯}{1}$ , 即得

$sin θ + sin φ = 2 sin \frac{θ + φ}{2} cos \frac{θ - φ}{2} .$

思考

如果不用 (1) 的结果, 如何证明?

例 8 的证明用到了换元的方法. 如把 $α + β$ 看作 $θ, α - β$ 看作 $φ$ , 从而把包含 $α, β$ 的三角函数式转化为 $θ, φ$ 的三角函数式. 或者, 把 $sin α cos β$ 看作 $x, cos α sin β$ 看作 $y$ , 把等式看作 $x, y$ 的方程, 则原问题转化为解方程 (组) 求 $x$ . 它们都体现了化归思想.

练习

求证: $tan \frac{α}{2} = \frac{sin α}{1 + cos α} = \frac{1 - cos α}{sin α}$ .

已知 $cos θ = \frac{1}{3}$ , 且 $27 0^{\circ} < θ < 36 0^{\circ}$ , 试求 $sin \frac{θ}{2}$ 和 $cos \frac{θ}{2}$ 的值.

已知等腰三角形的顶角的余弦等于 $\frac{7}{25}$ , 求这个三角形的一个底角的正切.

求证:
(1) $cos α sin β = \frac{1}{2} [sin (α + β) - sin (α - β)]$ ;
(2) $cos α cos β = \frac{1}{2} [cos (α + β) + cos (α - β)]$ ;
(3) $sin α sin β = - \frac{1}{2} [cos (α + β) - cos (α - β)]$ .

求证:
(1) $sin θ - sin φ = 2 cos \frac{θ + φ}{2} sin \frac{θ - φ}{2}$ ;
(2) $cos θ + cos φ = 2 cos \frac{θ + φ}{2} cos \frac{θ - φ}{2}$ ;
(3) $cos θ - cos φ = - 2 sin \frac{θ + φ}{2} sin \frac{θ - φ}{2}$ .

例 9

求下列函数的周期, 最大值和最小值:
(1) $y = sin x + 3 cos x$ ;
(2) $y = 3 sin x + 4 cos x$ .

分析：

便于求周期和最大值、最小值的三角函数式是 $y = A sin (x + φ)$ , 利用和角公式将其展开, 可化为 $y = a sin x + b cos x$ 的形式. 反之, 利用和（差）角公式, 可将 $y = a sin x + b cos x$ 转化为 $y = A sin (x + φ)$ 的形式, 进而就可以求得其周期和最值了.

解:

(1)

$y = sin x + 3 cos x = 2 (\frac{1}{2} sin x + \frac{3}{2} cos x)^{\overset{◯}{1}} = 2 (sin x cos \frac{π}{3} + cos x sin \frac{π}{3}) = 2 sin (x + \frac{π}{3}) .$

因此, 所求周期为 $2 π$ , 最大值为 2 , 最小值为 -2 .
(2) 设 $3 sin x + 4 cos x = A sin (x + φ)$ , 则

$3 sin x + 4 cos x = A sin x cos φ + A cos x sin φ .$

于是

$A cos φ = 3, A sin φ = 4,$

于是

$A^{2} cos^{2} φ + A^{2} sin^{2} φ = 25,$

所以

$A^{2} = 25 .$

取 $A = 5$ , 则 $cos φ = \frac{3}{5}, sin φ = \frac{4}{5}$ .

由 $y = 5 sin (x + φ)$ 可知, 所求周期为 $2 π$ , 最大值为 $5$ , 最小值为 $- 5$ .

思考

$\overset{◯}{1}$ 你能说说这一步变形的理由吗?

例 10

如图 5.5-2, 在扇形 $OPQ$ 中, 半径 $OP = 1$ , 圆心角 $∠ POQ = \frac{π}{3}, C$ 是扇形弧上的动点, 矩形 $A BC D$ 内接于扇形. 记 $∠ POC = α$ , 求当角 $α$ 取何值时, 矩形 $A BC D$ 的面积最大? 并求出这个最大面积.

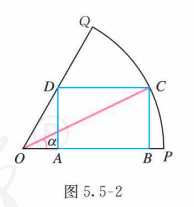
分析：

可先建立矩形 $A BC D$ 的面积 $S$ 与 $α$ 之间的函数关系 $S =$ $f (α)$ , 再求函数 $S = f (α)$ 的最大值.

解：

在 Rt $△ OBC$ 中, $OB = cos α, BC = sin α$ .
在 Rt $△ O A D$ 中, $\frac{D A}{O A} = tan \frac{π}{3} = 3$ .

所以

$O A = \frac{3}{3} D A = \frac{3}{3} BC = \frac{3}{3} sin α, A B = OB - O A = cos α - \frac{3}{3} sin α .$

设矩形 $A BC D$ 的面积为 $S$ , 则

$S = A B \cdot BC = (cos α - \frac{3}{3} sin α) sin α = sin α cos α - \frac{3}{3} sin^{2} α = \frac{1}{2} sin 2 α - \frac{3}{6} (1 - cos 2 α) = \frac{1}{2} sin 2 α + \frac{3}{6} cos 2 α - \frac{3}{6} = \frac{1}{3} (\frac{3}{2} sin 2 α + \frac{1}{2} cos 2 α) - \frac{3}{6} = \frac{1}{3} sin (2 α + \frac{π}{6}) - \frac{3}{6} .$

由 $0 < α < \frac{π}{3}$ , 得 $\frac{π}{6} < 2 α + \frac{π}{6} < \frac{5 π}{6}$ , 所以当 $2 α + \frac{π}{6} = \frac{π}{2}$ , 即 $α = \frac{π}{6}$ 时,

$S_{最大} = \frac{1}{3} - \frac{3}{6} = \frac{3}{6} .$

因此, 当 $α = \frac{π}{6}$ 时, 矩形 $A BC D$ 的面积最大, 最大面积为 $\frac{3}{6}$ .

由例 9 、例 10 可以看到, 通过三角恒等变换, 我们把 $y = a sin x + b cos x$ 转化为 $y = A sin (x + φ)$ 的形式, 这个过程中蕴含了化归思想.

练习

求下列函数的周期, 最大值和最小值:
(1) $y = 5 cos x - 12 sin x$ ;
(2) $y = cos x + 2 sin x$ .

要在半径为 $R$ 的圆形场地内建一个矩形的花坛, 应怎样截取, 才能使花坛的面积最大?

已知正 $n$ 边形的边长为 $a$ , 内切圆的半径为 $r$ , 外接圆的半径为 $R$ . 求证 $R + r = \frac{a}{2 tan \frac{π}{2 n}}$ .

习题 5.5

复习巩固

已知 $sin α = \frac{2}{3}, cos β = - \frac{3}{4}, α \in (\frac{π}{2}, π), β \in (π, \frac{3 π}{2})$ , 求 $cos (α - β)$ 的值.

已知 $α, β$ 都是锐角, $cos α = \frac{1}{7}, cos (α + β) = - \frac{11}{14}$ , 求 $cos β$ 的值. (提示: $β = (α + β) - α_{.}$ )

已知 $sin (3 0^{\circ} + α) = \frac{3}{5}, 6 0^{\circ} < α < 15 0^{\circ}$ , 求 $cos α$ 的值.

在 $△ A BC$ 中, $sin A = \frac{5}{13}, cos B = \frac{3}{5}$ , 求 $cos C$ 的值.

已知 $tan (α + β) = 3, tan (α - β) = 5$ , 求 $tan 2 α, tan 2 β$ 的值.

化简:
(1) $sin 34 7^{\circ} cos 14 8^{\circ} + sin 7 7^{\circ} cos 5 8^{\circ}$ ;
(2) $sin 16 4^{\circ} sin 22 4^{\circ} + sin 25 4^{\circ} sin 31 4^{\circ}$ ;
(3) $sin (α + β) cos (γ - β) - cos (β + α) sin (β - γ)$ ;
(4) $sin (α - β) sin (β - γ) - cos (α - β) cos (γ - β)$ ;
(5) $\frac{tan \frac{5 π}{4} + tan \frac{5 π}{12}}{1 - tan \frac{5 π}{12}}$ ;
(6) $\frac{sin ( α + β ) - 2 sin α cos β}{2 sin α sin β + cos ( α + β )}$ .

已知 $sin α = 0.80, α \in (0, \frac{π}{2})$ , 求 $sin 2 α, cos 2 α$ 的值（精确到 0.01 ).

求证:
(1) $(sin 2 α - cos 2 α)^{2} = 1 - sin 4 α$ ，
(2) $tan (\frac{x}{2} + \frac{π}{4}) + tan (\frac{x}{2} - \frac{π}{4}) = 2 tan x$ ;
(3) $\frac{1 + sin 2 φ}{cos φ + sin φ} = cos φ + sin φ$ ;
(4) $\frac{1 - 2 sin α cos α}{cos ^{2} α - sin ^{2} α} = \frac{1 - tan α}{1 + tan α}$ ;
(5) $\frac{1 - cos 2 θ}{1 + cos 2 θ} = tan^{2} θ$ ;
(6) $\frac{1 + sin 2 θ - cos 2 θ}{1 + sin 2 θ + cos 2 θ} = tan θ$ .

已知 $sin (α + β) = \frac{1}{2}, sin (α - β) = \frac{1}{3}$ , 求证:
(1) $sin α cos β = 5 cos α sin β$ ;
(2) $tan α = 5 tan β$ .

10.

已知 $\frac{1 - tan θ}{2 + tan θ} = 1$ , 求证 $tan 2 θ = - 4 tan (θ + \frac{π}{4})$ .

11.

已知一段圆弧所对的圆心角的正弦值等于 $\frac{3}{5}$ , 求这段圆弧所对的圆周角的正弦、余弦和正切.

12.

化简:
(1) $315 sin x + 35 cos x$ ;
(2) $\frac{3}{2} cos x - \frac{3}{2} sin x$ ;
(3) $3 sin \frac{x}{2} + cos \frac{x}{2}$ ;
(4) $\frac{2}{4} sin (\frac{π}{4} - x) + \frac{6}{4} cos (\frac{π}{4} - x)$ .

综合运用

13.

在 $△ A BC$ 中, 已知 $tan A, tan B$ 是 $x$ 的方程 $x^{2} + p (x + 1) + 1 = 0$ 的两个实根, 求 $∠ C$ .

14.

在 $△ A BC$ 中, $B = \frac{π}{4}, BC$ 边上的高等于 $\frac{1}{3} BC$ , 则 $cos A = ()$ .
(A) $\frac{3 10}{10}$
(B) $\frac{10}{10}$
(C) $- \frac{10}{10}$
(D) $- \frac{3 10}{10}$

15.

求证:
(1) $3 + cos 4 α - 4 cos 2 α = 8 sin^{4} α$ ;
(2) $\frac{tan α tan 2 α}{tan 2 α - tan α} + 3 (sin^{2} α - cos^{2} α) = 2 sin (2 α - \frac{π}{3})$ .

16.

是否存在锐角 $α, β$ , 使 $α + 2 β = \frac{2 π}{3}, tan \frac{α}{2} tan β = 2 - 3$ 同时成立? 若存在, 求出 $α, β$ 的度数; 若不存在, 请说明理由.

17.

(1) 求函数 $f (x) = sin (\frac{π}{3} + 4 x) + sin (4 x - \frac{π}{6})$ 的周期和单调递增区间;
(2) 求函数 $f (x) = a sin x + b cos x (a^{2} + b^{2} \neq = 0)$ 的最大值和最小值.

拓广探索

18.

观察以下各等式:

$sin^{2} 3 0^{\circ} + cos^{2} 6 0^{\circ} + sin 3 0^{\circ} cos 6 0^{\circ} = \frac{3}{4}, sin^{2} 2 0^{\circ} + cos^{2} 5 0^{\circ} + sin 2 0^{\circ} cos 5 0^{\circ} = \frac{3}{4}, sin^{2} 1 5^{\circ} + cos^{2} 4 5^{\circ} + sin 1 5^{\circ} cos 4 5^{\circ} = \frac{3}{4} .$

分析上述各式的共同特点, 写出能反映一般规律的等式, 并对等式的正确性作出证明.

19.

你能利用所给图形, 证明下列两个等式吗?

$\frac{1}{2} (sin α + sin β) = sin \frac{α + β}{2} cos \frac{α - β}{2}; \frac{1}{2} (cos α + cos β) = cos \frac{α + β}{2} cos \frac{α - β}{2} .$

20.

设 $f (α) = sin^{x} α + cos^{x} α, x \in {n ∣ n = 2 k, k \in N_{+}}$ . 利用三角变换, 估计 $f (α)$ 在 $x = 2, 4, 6$ 时的取值情况, 进而猜想 $x$ 取一般值时 $f (α)$ 的取值范围.