7.3 复数的三角表示

2024-06-21 22:23:20 新建

选学内容, 不作考试要求.

前面我们研究了复数 $a + b i$ 及其四则运算, 本节研究复数的另一种重要表示 —— 复数的三角表示. 它可以帮助我们进一步认识复数, 同时能给复数的运算带来便利.

7.3.1 复数的三角表示式

我们知道, 复数可以用 $a + b i (a, b \in R)$ 的形式来表示, 复数 $a + b i$ 与复平面内的点 $Z (a, b)$ 是一一对应的, 与平面向量 $OZ = (a, b)$ 也是一一对应的. 借助复数的几何意义,复数能不能用其他形式来表示呢?

探究

如图 7.3-1, 复数 $z = a + b i$ 与向量 $OZ = (a, b)$ 一一对应,复数 $z$ 由向量 $OZ$ 的坐标 $(a, b)$ 唯一确定. 我们知道向量也可以由它的大小和方向唯一确定, 那么能否借助向量的大小和方向这两个要素来表示复数呢? 如何表示?

答

向量的大小可以用模来刻画, 那么向量的方向如何刻画呢? 由图 7.3-1 容易想到, 可以借助以 $x$ 轴的非负半轴为始边, 以向量 $OZ$ 所在射线（射线 $OZ$ ）为终边的角 $θ$ 来刻画 $OZ$ 的方向.

思考

你能用向量 $OZ$ 的模和角 $θ$ 来表示复数 $z$ 吗?

答

记向量的模 $∣ OZ ∣ = ∣ a + b i ∣ = r$ , 由图 7.3-1 可以得到,

${a = r cos θ, b = r sin θ$

所以

$a + b i = r cos θ + i r sin θ = r (cos θ + i sin θ),$

其中

$r = a^{2} + b^{2}, cos θ = \frac{a}{r}, sin θ = \frac{b}{r} .$

这样, 我们就用刻画向量大小的模 $r$ 和刻画向量方向的角 $θ$ 表示了复数 $z$ .

思考

当点 $Z$ 在实轴或虚轴上时, 这个结论成立吗?

定义三角表示式代数表示式

一般地, 任何一个复数 $z = a + b i$ 都可以表示成

$r (cos θ + i sin θ)$

的形式. 其中, $r$ 是复数 $z$ 的模; $θ$ 是以 $x$ 轴的非负半轴为始边, 向量 $OZ$ 所在射线 (射线 $OZ$ ) 为终边的角, 叫做复数 $z = a + b i$ 的辐角 (argument of a complex number). $r (cos θ + i sin θ)$ 叫做复数 $z = a + b i$ 的三角表示式, 简称三角形式. 为了与三角形式区分开来, $a + b i$ 叫做复数的代数表示式, 简称代数形式.

定义辐角的主值

显然, 任何一个不为零的复数的辐角有无限多个值, 且这些值相差 $2 π$ 的整数倍. 例如, 复数 $i$ 的辐角是 $\frac{π}{2} + 2 kπ$ , 其中 $k$ 可以取任何整数. 对于复数 0 , 因为它对应着零向量,而零向量的方向是任意的, 所以复数 0 的辐角也是任意的. 我们规定在 $0 ⩽ θ < 2 π$ 范围内的

辐角 $θ$ 的值为辐角的主值. 通常记作 $ar g z$ , 即 $0 ⩽ ar g z < 2 π$ . 例如, $ar g 1 = 0, ar g i = \frac{π}{2}$ , $ar g (- 1) = π, ar g (- i) = \frac{3 π}{2}$

复数的代数形式可以转化为三角形式, 三角形式也可以转化为代数形式. 我们可以根据运算的需要, 将复数的三角形式和代数形式进行互化.

例 1

画出下列复数对应的向量, 并把这些复数表示成三角形式:
(1) $\frac{1}{2} + \frac{3}{2} i$ ;
(2) $1 - i$ .
分析: 只要确定复数的模和一个辐角, 就能将复数的代数形式转化为三角形式.

解:

(1) 复数 $\frac{1}{2} + \frac{3}{2} i$ 对应的向量如图 7.3-2 所示, 则

$r = (\frac{1}{2})^{2} + (\frac{3}{2})^{2} = 1, cos θ = \frac{1}{2} .$

因为与 $\frac{1}{2} + \frac{3}{2} i$ 对应的点在第一象限, 所以 $ar g (\frac{1}{2} + \frac{3}{2} i) = \frac{π}{3}$ .
于是 $\frac{1}{2} + \frac{3}{2} i = cos \frac{π}{3} + i sin \frac{π}{3}$ .

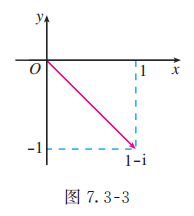
(2) 复数 $1 - i$ 对应的向量如图 7.3-3 所示，则

$r = 1^{2} + (- 1)^{2} = 2, cos θ = \frac{1}{2} = \frac{2}{2} .$

因为与 $1 - i$ 对应的点在第四象限, 所以 $ar g (1 - i) = \frac{7 π}{4}$ .
于是 $1 - i = 2 (cos \frac{7 π}{4} + i sin \frac{7 π}{4})$ .

当然, 把一个复数表示成三角形式时, 辐角 $θ$ 不一定取主值.

例如 $2 [cos (- \frac{π}{4}) + i sin (- \frac{π}{4})]$ 也是 $1 - i$ 的三角形式.

例 2

分别指出下列复数的模和一个辐角, 画出它们对应的向量, 并把这些复数表示成代数形式:
(1) $cos π + i sin π$ ;
(2) $6 (cos \frac{11 π}{6} + i sin \frac{11 π}{6})$ .

解:

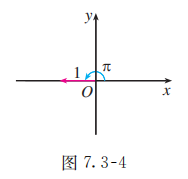
(1) 复数 $cos π + i sin π$ 的模 $r = 1$ , 一个辐角 $θ =$ $π$ , 对应的向量如图 7.3-4 所示. 所以

$cos π + i sin π = - 1 + 0 i = - 1.$

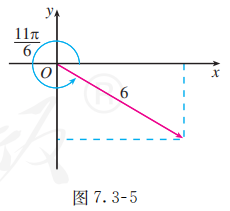
(2) 复数 $6 (cos \frac{11 π}{6} + i sin \frac{11 π}{6})$ 的模 $r = 6$ , 一个辐角 $θ = \frac{11 π}{6}$ , 对应的向量如图 7.3-5 所示. 所以

$6 (cos \frac{11 π}{6} + i sin \frac{11 π}{6}) = 6 cos \frac{11 π}{6} + (6 sin \frac{11 π}{6}) i = 6 \times \frac{3}{2} + 6 \times (- \frac{1}{2}) i = 33 - 3 i .$

思考

两个用三角形式表示的复数在什么条件下相等?

答

每一个不等于零的复数有唯一的模与辐角的主值, 并且由它的模与辐角的主值唯一确定. 因此, 两个非零复数相等当且仅当它们的模与辐角的主值分别相等.

练习

画出下列复数对应的向量, 并把这些复数表示成三角形式:
(1) 4 ;
(2) $- i$ ;
(3) $23 + 2 i$ ;
(4) $- \frac{1}{2} - \frac{3}{2} i$ .

下列复数是不是三角形式? 如果不是, 把它们表示成三角形式.
(1) $\frac{1}{2} (cos \frac{π}{4} - i sin \frac{π}{4})$ ;
(2) $- \frac{1}{2} (cos \frac{π}{3} + i sin \frac{π}{3})$ ;
(3) $\frac{1}{2} (sin \frac{5 π}{12} + i cos \frac{5 π}{12})$ ;
(4) $cos \frac{7 π}{5} + i sin \frac{7 π}{5}$ ;
(5) $2 (cos \frac{π}{3} + i sin \frac{π}{6})$ .

把下列复数表示成代数形式:
(1) $6 (cos \frac{3 π}{2} + i sin \frac{3 π}{2})$ ;
(2) $2 (cos \frac{5 π}{3} + i sin \frac{5 π}{3})$ .

7.3.2 复数乘、除运算的三角表示及其几何意义

前面, 我们研究了复数代数形式的乘、除运算, 下面我们利用复数的三角表示研究复数的乘、除运算及其几何意义.

思考

如果把复数 $z_{1}, z_{2}$ 分别写成三角形式 $z_{1} = r_{1} (cos θ_{1} + i sin θ_{1}), z_{2} = r_{2} (cos θ_{2} +$ isin $θ_{2}$ ), 你能计算 $z_{1} z_{2}$ 并将结果表示成三角形式吗?

答

根据复数的乘法法则以及两角和的正弦、余弦公式, 可以得到

$z_{1} z_{2} = r_{1} (cos θ_{1} + i sin θ_{1}) \cdot r_{2} (cos θ_{2} + i sin θ_{2}) = r_{1} r_{2} (cos θ_{1} + i sin θ_{1}) (cos θ_{2} + i sin θ_{2}) = r_{1} r_{2} [(cos θ_{1} cos θ_{2} - sin θ_{1} sin θ_{2}) + i (sin θ_{1} cos θ_{2} + cos θ_{1} sin θ_{2})] = r_{1} r_{2} [cos (θ_{1} + θ_{2}) + i sin (θ_{1} + θ_{2})],$

即

定理

$= r_{1} (cos θ_{1} + i sin θ_{1}) \cdot r_{2} (cos θ_{2} + i sin θ_{2}) r_{1} r_{2} [cos (θ_{1} + θ_{2}) + i sin (θ_{1} + θ_{2})] .$

这就是说,
两个复数相乘, 积的模等于各复数的模的积, 积的辐角等于各复数的辐角的和.

探究

由复数乘法运算的三角表示, 你能得到复数乘法的几何意义吗?

答

两个复数 $z_{1}, z_{2}$ 相乘时, 可以像图 7.3-6 那样, 先分别画出与 $z_{1}, z_{2}$ 对应的向量 $O Z_{1}, O Z_{2}$ , 然后把向量 $O Z_{1}$ 绕点 $O$ 按逆时针方向旋转角 $θ_{2}$ (如果 $θ_{2} < 0$ , 就要把 $O Z_{1}$ 绕点 $O$ 按顺时针方向旋转角 $∣ θ_{2} ∣)$ , 再把它的模变为原来的 $r_{2}$ 倍, 得到向量 $OZ, OZ$ 表示的复数就是积 $z_{1} z_{2}$ . 这是复数乘法的几何意义.

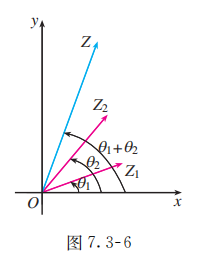
思考

你能解释 $i^{2} = - 1$ 和 $(- 1)^{2} = 1$ 的几何意义吗?

例 3

已知 $z_{1} = \frac{3}{2} (cos \frac{π}{6} + i sin \frac{π}{6}), z_{2} = 2 (cos \frac{π}{3} + i sin \frac{π}{3})$ ,求 $z_{1} z_{2}$ , 请把结果化为代数形式, 并作出几何解释.

解:

$z_{1} z_{2} = \frac{3}{2} (cos \frac{π}{6} + i sin \frac{π}{6}) \times 2 (cos \frac{π}{3} + i sin \frac{π}{3}) = \frac{3}{2} \times 2 [cos (\frac{π}{6} + \frac{π}{3}) + i sin (\frac{π}{6} + \frac{π}{3})] = 3 (cos \frac{π}{2} + i sin \frac{π}{2}) = 3 i .$

首先作与 $z_{1}, z_{2}$ 对应的向量 $O Z_{1}, O Z_{2}$ , 然后把向量 $O Z_{1}$ 绕点 $O$ 按逆时针方向旋转 $\frac{π}{3}$ , 再将其长度伸长为原来的 2 倍, 这样得到一个长度为 3 , 辐角为 $\frac{π}{2}$ 的向量 $OZ$ (图 7.3-7). $OZ$ 即为积 $z_{1} z_{2} = 3 i$ 所对应的向量.

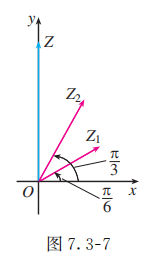
当不要求把计算结果化为代数形式时, 也可以用三角形式表示.

例 4

如图 7.3-8, 向量 $OZ$ 对应的复数为 $1 +$ $i$ , 把 $OZ$ 绕点 $O$ 按逆时针方向旋转 $12 0^{\circ}$ , 得到 $O Z^{'}$ .求向量 $O Z^{'}$ 对应的复数 (用代数形式表示).

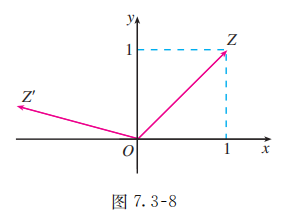
分析:

根据复数乘法的几何意义, 向量 $O Z^{'}$ 对应的复数是复数 $1 + i$ 与 $z_{0}$ 的积, 其中复数 $z_{0}$ 的模是 1 , 辐角的主值是 $12 0^{\circ}$ .

解:

向量 $O Z^{'}$ 对应的复数为

$= = (1 + i) (cos 12 0^{\circ} + i sin 12 0^{\circ}) (1 + i) (- \frac{1}{2} + \frac{3}{2} i) \frac{- 1 - 3}{2} + \frac{3 - 1}{2} i .$

探究

复数的除法运算是乘法运算的逆运算. 根据复数乘法运算的三角表示, 你能得出复数除法运算的三角表示吗?

答

设 $z_{1} = r_{1} (cos θ_{1} + i sin θ_{1}), z_{2} = r_{2} (cos θ_{2} + i sin θ_{2})$ , 且 $z_{2} \neq = 0$ , 因为

$r_{2} (cos θ_{2} + i sin θ_{2}) \cdot \frac{r _{1}}{r _{2}} [cos (θ_{1} - θ_{2}) + i sin (θ_{1} - θ_{2})] = r_{1} (cos θ_{1} + i sin θ_{1}),$

所以根据复数除法的定义, 有

定理

$\frac{r _{1} ( cos θ _{1} + i sin θ _{1} )}{r _{2} ( cos θ _{2} + i sin θ _{2} )} = \frac{r _{1}}{r _{2}} [cos (θ_{1} - θ_{2}) + i sin (θ_{1} - θ_{2})] .$

这就是说, 两个复数相除, 商的模等于被除数的模除以除数的模所得的商, 商的辐角等于被除数的辐角减去除数的辐角所得的差.

探究

类比复数乘法的几何意义, 由复数除法运算的三角表示, 你能得出复数除法的几何意义吗?

例 5

计算 $4 (cos \frac{4 π}{3} + i sin \frac{4 π}{3}) \div [2 (cos \frac{5 π}{6} + i sin \frac{5 π}{6})]$ , 并把结果化为代数形式.

解:

$原式 = 2 [cos (\frac{4 π}{3} - \frac{5 π}{6}) + i sin (\frac{4 π}{3} - \frac{5 π}{6})] = 2 (cos \frac{π}{2} + i sin \frac{π}{2}) = 2 (0 + i) = 2 i .$

练习

计算:
(1) $8 (cos \frac{π}{6} + i sin \frac{π}{6}) \times 2 (cos \frac{π}{4} + i sin \frac{π}{4})$ ;
(2) $2 (cos \frac{4 π}{3} + i sin \frac{4 π}{3}) \times 4 (cos \frac{5 π}{6} + i sin \frac{5 π}{6})$ ;
(3) $2 (cos 24 0^{\circ} + i sin 24 0^{\circ}) \times \frac{3}{2} (cos 6 0^{\circ} + i sin 6 0^{\circ})$ ;
(4) $3 (cos 1 8^{\circ} + i sin 1 8^{\circ}) \times 2 (cos 5 4^{\circ} + i sin 5 4^{\circ}) \times 5 (cos 10 8^{\circ} + i sin 10 8^{\circ})$ .

计算:
(1) $12 (cos \frac{7 π}{4} + i sin \frac{7 π}{4}) \div [6 (cos \frac{2 π}{3} + i sin \frac{2 π}{3})]$ ;
(2) $3 (cos 15 0^{\circ} + i sin 15 0^{\circ}) \div [2 (cos 22 5^{\circ} + i sin 22 5^{\circ})]$ ;
(3) $2 \div (cos \frac{π}{4} + i sin \frac{π}{4})$ ;
(4) $- i \div [2 (cos 12 0^{\circ} + i sin 12 0^{\circ})]$ .

在复平面内, 把与复数 $3 - 3 i$ 对应的向量绕原点 $O$ 按顺时针方向旋转 $6 0^{\circ}$ , 求与所得的向量对应的复数 (用代数形式表示).

习题 7.3

复习巩固

画出下列复数对应的向量, 并把这些复数表示成三角形式:
(1) 6 ;
(2) $1 + i$ ;
(3) $1 - 3 i$ ;
(4) $- \frac{3}{2} + \frac{1}{2} i$ .

把下列复数表示成代数形式:
(1) $32 (cos \frac{π}{4} + i sin \frac{π}{4})$ ;
(2) $8 (cos \frac{11 π}{6} + i sin \frac{11 π}{6})$ ;
(3) $9 (cos π + i sin π)$ ;
(4) $6 (cos \frac{4 π}{3} + i sin \frac{4 π}{3})$ .

计算:
(1) $3 (cos \frac{π}{3} + i sin \frac{π}{3}) \times 3 (cos \frac{π}{6} + i sin \frac{π}{6})$ ;
(2) $10 (cos \frac{π}{2} + i sin \frac{π}{2}) \times 2 (cos \frac{π}{4} + i sin \frac{π}{4})$ ;
(3) $10 (cos \frac{2 π}{3} + i sin \frac{2 π}{3}) \div [5 (cos \frac{π}{3} + i sin \frac{π}{3})]$ ;
(4) $12 (cos \frac{3 π}{2} + i sin \frac{3 π}{2}) \div [6 (cos \frac{π}{6} + i sin \frac{π}{6})]$ .

计算下列各式, 并作出几何解释:
(1) $2 (cos \frac{2 π}{3} + i sin \frac{2 π}{3}) \times 22 (cos \frac{π}{3} + i sin \frac{π}{3})$ ;
(2) $2 (cos 7 5^{\circ} + i sin 7 5^{\circ}) \times (\frac{1}{2} - \frac{1}{2} i)$ ;
(3) $4 (cos 30 0^{\circ} + i sin 30 0^{\circ}) \div [2 (cos \frac{3 π}{4} + i sin \frac{3 π}{4})]$ ;
(4) $(- \frac{1}{2} + \frac{3}{2} i) \div [2 (cos \frac{π}{3} + i sin \frac{π}{3})]$ .

综合运用

(1) 求证 $\frac{1}{cos θ + i sin θ} = cos θ - i sin θ$ ;
(2) 写出下列复数 $z$ 的倒数 $\frac{1}{z}$ 的模与辐角:

$z = 4 (cos \frac{π}{12} + i sin \frac{π}{12}), z = cos \frac{π}{6} - i sin \frac{π}{6}, z = \frac{2}{2} (1 - i) .$

求证:
(1) $(cos 7 5^{\circ} + i sin 7 5^{\circ}) (cos 1 5^{\circ} + i sin 1 5^{\circ}) = i$ ;
(2) $(cos 3 θ - i sin 3 θ) (cos 2 θ - i sin 2 θ) = cos 5 θ - i sin 5 θ$ .

化简:
(1) $\frac{( cos 7 θ + i sin 7 θ ) ( cos 2 θ + i sin 2 θ )}{( cos 5 θ + i sin 5 θ ) ( cos 3 θ + i sin 3 θ )}$ ;
(2) $\frac{cos φ - i sin φ}{cos φ + i sin φ}$ .

设 $z = 3 - i$ 对应的向量为 $OZ$ , 将 $OZ$ 绕点 $O$ 按逆时针方向和顺时针方向分别旋转 $4 5^{\circ}$ 和 $6 0^{\circ}$ ,求所得向量对应的复数 (用代数形式表示).

拓广探索

如图, 复平面内的 $△ A BC$ 是等边三角形, 它的两个顶点 $A, B$ 的坐标分别为 $(1, 0)$ , $(2, 1)$ , 求点 $C$ 的坐标.

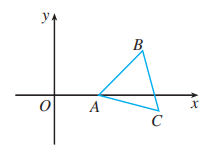
10.

如图, 已知平面内并列的三个全等的正方形, 利用复数证明

$∠1 + ∠2 + ∠3 = \frac{π}{2} .$

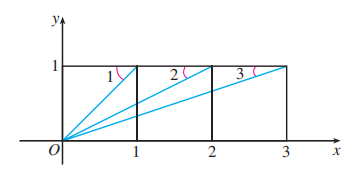
探究与发现

1 的 $n$ 次方根

初中我们学过, 1 的平方根为 $\pm 1$ , 它们互为相反数. 如何求 1 的 3 次方根, 4 次方根 $\dots\dots . n$ 次方根? 它们有什么性质呢?

我们知道开方是乘方的逆运算, 为了探求 1 的 $n$ 次方根, 需要先研究复数的乘方.

由复数乘法运算的三角表示知, 若 $z_{1} = r_{1} (cos θ_{1} + i sin θ_{1}), z_{2} = r_{2} \cdot (cos θ_{2} +$ $i sin θ_{2})$ , 则 $z_{1} z_{2} = r_{1} r_{2} [cos (θ_{1} + θ_{2}) + i sin (θ_{1} + θ_{2})]$ . 这个结论可以推广到 $n (n ⩾ 2, n \in N)$ 个复数相乘的情况, 即若 $z_{1} = r_{1} (cos θ_{1} + i sin θ_{1}), z_{2} = r_{2} (cos θ_{2} +$ $i sin θ_{2}), \dots, z_{n} = r_{n} (cos θ_{n} + i sin θ_{n})$ , 则

$z_{1} z_{2} \dots z_{n} = r_{1} r_{2} \dots r_{n} [cos (θ_{1} + θ_{2} + \dots + θ_{n}) + i sin (θ_{1} + θ_{2} + \dots + θ_{n})] .$

特别地, 如果 $z_{1} = z_{2} = \dots = z_{n} = r (cos θ + i sin θ)$ , 那么

$[r (cos θ + i sin θ)]^{n} = r^{n} (cos n θ + i sin n θ) .$

这就是说, 复数的 $n (n \in N^{*})$ 次幂的模等于这个复数的模的 $n$ 次幂, 它的辐角等于这个复数的辐角的 $n$ 倍, 这个结论叫做棣莫弗定理.

下面我们利用棣莫弗定理, 探求 1 的 3 次方根,给出它们的几何解释, 并探求它们的性质.

思考

类比复数乘法的几何意义, 你能给出复数乘方的几何意义吗?

设 $z = ρ (cos φ + i sin φ) (ρ > 0)$ 是 1 的 3 次方根, 则 $z^{3} = 1 = cos 0 + i sin 0$ , 从而

$[ρ (cos φ + i sin φ)]^{3} = ρ^{3} (cos 3 φ + i sin 3 φ) = cos 0 + i sin 0.$

因为相等的复数的模相等, 辐角可以相差 $2 π$ 的整数倍, 所以

${ρ^{3} = 1, 3 φ = 0 + 2 kπ (k \in Z),$

即

${ρ = 1, φ = \frac{2 kπ}{3} (k \in Z) .$

因此 1 的 3 次方根是 $cos \frac{2 kπ}{3} + i sin \frac{2 kπ}{3} (k \in Z)$ .

根据三角函数的周期性可得, 1 的 3 次方根为 $ω_{k} = cos \frac{2 kπ}{3} + i sin \frac{2 kπ}{3} (k = 0, 1, 2)$ , 即 $ω_{0} = cos 0 + i sin 0 = 1$ , $ω_{1} = cos \frac{2 π}{3} + i sin \frac{2 π}{3} = - \frac{1}{2} + \frac{3}{2} i$ , $ω_{2} = cos \frac{4 π}{3} + i sin \frac{4 π}{3} = - \frac{1}{2} - \frac{3}{2} i$ .

1 的 3 次方根的几何意义是什么呢?

如图 1, 在复平面内, 设 $ω_{0}, ω_{1}, ω_{2}$ 对应的点分别为 $Z_{0}, Z_{1}, Z_{2}$ , 对应的向量分别为 $O Z_{0}, O Z_{1}, O Z_{2}$ . 因为 $∣ ω_{0} ∣ = ∣ ω_{1} ∣ = ∣ ω_{2} ∣ = 1$ , 所以 $ω_{0}, ω_{1}, ω_{2}$ 所对应的点 $Z_{0}, Z_{1}, Z_{2}$ 都在以原点 $O$ 为圆心的单位圆上. 因为 $ω_{0}$ , $ω_{1}, ω_{2}$ 的辐角依次相差 $\frac{2 π}{3}$ , 所以 $Z_{0}, Z_{1}, Z_{2}$ 是单位圆的三等分点（也可以看成单位圆的内接正三角形的顶点）,且分点 $Z_{0}$ 恰为单位圆与实轴的正半轴的交点.

从 $ω_{0}, ω_{1}, ω_{2}$ 对应的向量 $O Z_{0}, O Z_{1}, O Z_{2}$ 来看, 容易发现: 将 $O Z_{0}$ 绕原点 $O$ 按逆时针方向旋转 $\frac{2 π}{3}$ 得到 $O Z_{1}$ , 再按逆时针方向旋转 $\frac{2 π}{3}$ 得到 $O Z_{2}$ , 继续按逆时针方向旋转 $\frac{2 π}{3}$ 得到 $O Z_{0}$ .

我们还可以得到 1 的 3 次方根的一些性质:
(1) $(ω_{k})^{3} = 1, ∣ ω_{k} ∣ = 1$ , 其中 $k = 0, 1, 2$ ;
(2) $ω_{1}$ 和 $ω_{2}$ 互为共轭复数;
(3) $1 + ω_{k} + ω_{k}^{2} = 0 (k = 1, 2)$ .

你能证明这些性质吗?
类比上述研究方法, 请你自己探求 1 的 4 次方根, 5 次方根 $\dots\dots n$ 次方根. 你能解释它们的几何意义, 并探求它们的性质吗?