3.2 函数的基本性质
2024-01-31 22:28:20 新建
变化中的不变性就是性质, 变化中的规律性也是性质.
前面学习了函数的定义和表示法, 知道函数 描述了客观世界中变量之间的一种对应关系. 这样, 我们就可以通过研究函数的变化规律来把握客观世界中事物的变化规律. 因此, 研究函数的性质, 如随着自变量的增大函数值是增大还是减小, 有没有最大值或最小值, 函数图象有什么特征等, 是认识客观规律的重要方法.
思考
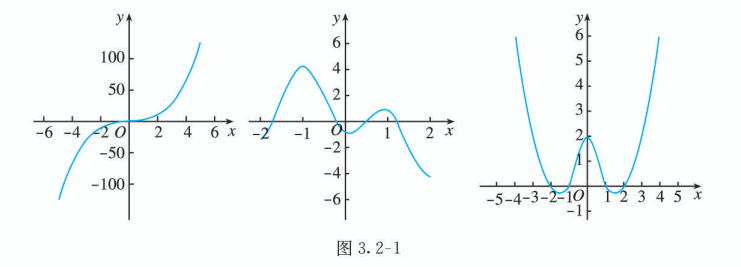
我们知道, 先画出函数图象, 通过观察和分析图象的特征, 可以得到函数的一些性质. 观察图 3.2-1 中的各个函数图象, 你能说说它们分别反映了相应函数的哪些性质吗?
3.2.1 单调性与最大(小)值
在初中, 我们利用函数图象研究过函数值随自变量的增大而增大 (或减小) 的性质, 这一性质叫做函数的单调性. 下面进一步用符号语言刻画这种性质.
例子
先研究二次函数 的单调性.
画出它的图象 (如图 3.2-2), 可以看到:
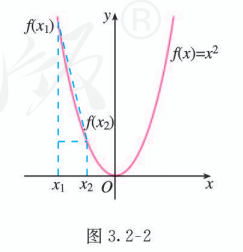
图象在 轴左侧部分从左到右是下降的, 也就是说,当 时, 随 的增大而减小. 用符号语言描述, 就是任意取 , 得到 ,那么当 时, 有 . 这时我们就说函数 在区间 上是单调递减的.
你能说明为什么 吗?
图象在 轴右侧部分从左到右是上升的,也就是说,当 时, 随 的增大而增大. 用符号语言表达, 就是任意取 , 得到 ,那么当 时, 有 . 这时我们就说函数 在区间 上是单调递增的.
你能说明为什么 吗?
思考
函数 各有怎样的单调性?
定义 单调性
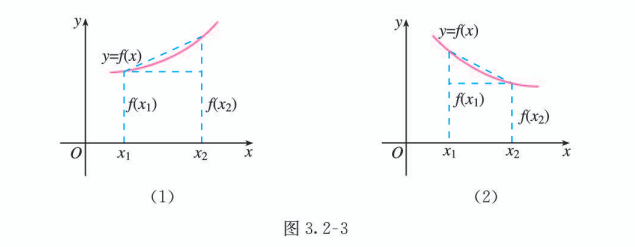
一般地, 设函数 的定义域为 , 区间 :
如果 , 当 时, 都有 , 那么就称函数 在区间 上单调递增 (图 3.2-3 (1)).
特别地, 当函数 在它的定义域上单调递增时, 我们就称它是增函数(increasing function).
如果 , 当 时, 都有 , 那么就称函数 在区间 上单调递减 (图 3.2-3(2)).
特别地, 当函数 在它的定义域上单调递减时, 我们就称它是减函数 (decreasing function).
如果函数 在区间 上单调递增或单调递减, 那么就说函数 在这一区间具有(严格的)单调性,区间 叫做 的单调区间.
思考
(1) 设 是区间 上某些自变量的值组成的集合,而且 , 当 时, 都有 , 我们能说函数 在区间 上单调递增吗? 你能举例说明吗?
(2) 函数的单调性是对定义域内某个区间而言的, 你能举出在整个定义域内是单调递增的函数例子吗? 你能举出在定义域内的某些区间上单调递增但在另一些区间上单调递减的函数例子吗?
其实就是列举一些特殊的例子来对定义加强理解。
例 1
根据定义, 研究函数 的单调性.
分析:
根据函数单调性的定义, 需要考察当 时, 还是 . 根据实数大小关系的基本事实, 只要考察 与 的大小关系.
解:
函数 的定义域是 . , 且 , 则
由 , 得 . 所以
(1) 当 时, . 于是
即
这时, 是增函数.
(2) 当 时, . 于是
即
这时, 是减函数.
在初中,我们利用函数图象得到了上述结论,这里用严格的推理运算得到了函数 的单调性.
例 2
物理学中的玻意耳定律 ( 为正常数) 告诉我们, 对于一定量的气体,当其体积 减小时, 压强 将增大. 试对此用函数的单调性证明.
分析:
根据题意, 只要证明函数 是减函数即可.
证明:
, 且 , 则
由 , 得 ;
由 , 得 .
又 , 于是
即
所以, 根据函数单调性的定义, 函数 是减函数. 也就是说, 当体积 减小时, 压强 将增大.
例 3
根据定义证明函数 在区间 上单调递增.
证明:
, 且 , 有
由 , 得 .
所以
又由 , 得 .
于是
即
所以, 函数 在区间 上单调递增.
练习
1.
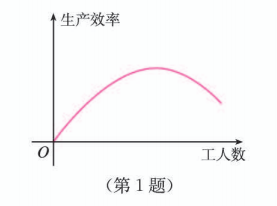
请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.
2.
根据定义证明函数 是增函数.
3.
证明函数 在区间 上单调递增.
4.
画出反比例函数 的图象.
(1) 这个函数的定义域 是什么?
(2) 它在定义域 上的单调性是怎样的? 证明你的结论.
通过观察图象, 先对函数是否具有某种性质做出猜想, 然后通过逻辑推理, 证明这种猜想的正确性, 是研究函数性质的一种常用方法.
再来观察本节的图 3.2-2, 可以发现, 二次函数 的图象上有一个最低点 , 即 , 都有 . 当一个函数 的图象有最低点时, 我们就说函数 有最小值.
思考
你能以函数 为例说明函数 的最大值的含义吗?
定义 最大值
一般地, 设函数 的定义域为 , 如果存在实数 满足:
(1) , 都有 ;
(2) ,使得 .
那么, 我们称 是函数 的最大值 (maximum value).
思考
你能仿照函数最大值的定义,给出函数 的最小值(minimum value)的定义吗?
例 4
“菊花” 烟花是最壮观的烟花之一. 制造时一般是期望在它达到最高点时爆裂. 如果烟花距地面的高度 (单位: ) 与时间 (单位: ) 之间的关系为 , 那么烟花冲出后什么时候是它爆裂的最佳时刻? 这时距地面的高度是多少 (精确到 )?
解:
画出函数 的图象 (图 3.2-4).显然, 函数图象的顶点就是烟花上升的最高点, 顶点的横坐标就是烟花爆裂的最佳时刻, 纵坐标就是这时距地面的高度.
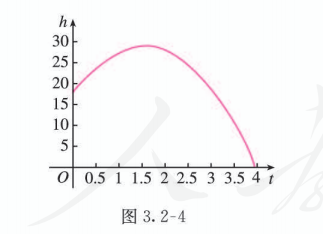
由二次函数的知识, 对于函数 , 我们有:
当 时, 函数有最大值
于是, 烟花冲出后 是它爆裂的最佳时刻, 这时距地面的高度约为 .
烟花设计者就是按照这些数据设定引信的长度, 以达到施放烟花的最佳效果.
例 5
已知函数 , 求函数的最大值和最小值.
分析:由函数 的图象(图 3.2-5) 可知, 函数 在区间 上单调递减.所以, 函数 在区间 的两个端点上分别取得最大值和最小值.
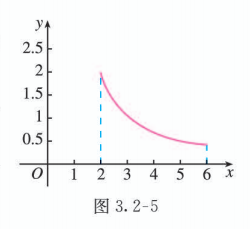
解:
, 且 , 则
由 , 得 ,于是
即
所以, 函数 在区间 上单调递减.
因此, 函数 在区间 的两个端点上分别取得最大值与最小值. 在 时取得最大值, 最大值是 2 ; 在 时取得最小值, 最小值是 0.4 .
练习
1.
整个上午 天气越来越暖, 中午时分 一场暴风雨使天气骤然凉爽了许多. 暴风雨过后, 天气转暖, 直到太阳落山 才又开始转凉. 画出这一天 期间气温作为时间函数的一个可能的图象 (示意图), 并说出所画函数的单调区间.
2.
设函数 的定义域为 . 如果 在区间 上单调递减, 在区间 上单调递增, 画出 的一个大致的图象, 从图象上可以发现 是函数 的一个 _ _ _
3.
已知函数 , 求函数在区间 上的最大值和最小值.
3.2.2 奇偶性
前面我们用符号语言精确地描述了函数图象在定义域的某个区间上 “上升”(或 “下降”)的性质. 下面继续研究函数的其他性质.
思考
画出并观察函数 和 的图象 (图 3.2-6), 你能发现这两个函数图象有什么共同特征吗?
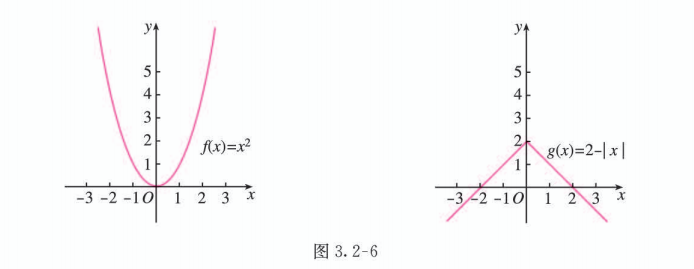
回答
可以发现, 这两个函数的图象都关于 轴对称.
探究
类比函数单调性, 你能用符号语言精确地描述 “函数图象关于 轴对称” 这一特征吗?
探究过程
不妨取自变量的一些特殊值, 观察相应函数值的情况, 如表 3.2-1.
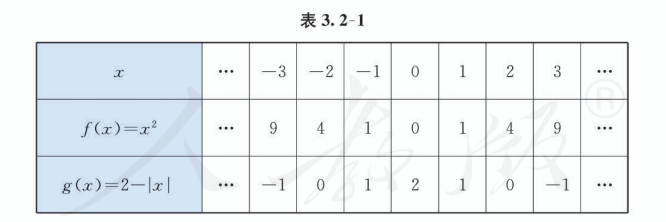
可以发现, 当自变量取一对相反数时, 相应的两个函数值相等.
例如, 对于函数 , 有
实际上, , 都有 , 这时称函数 为偶函数.
思考
请你仿照这个过程,说明函数 也是偶函数.
偶函数
一般地, 设函数 的定义域为 , 如果 , 都有 , 且 , 那么函数 就叫做偶函数 (even function).
例子
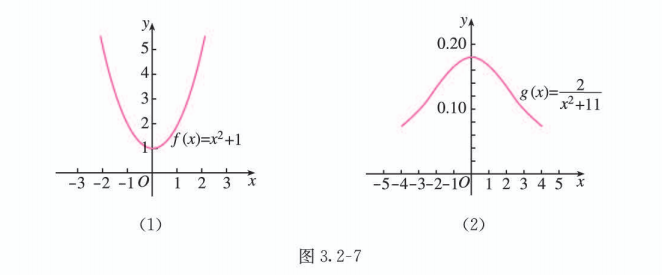
例如, 函数 都是偶函数, 它们的图象分别如图 3.2-7 (1)(2) 所示.
探究
观察函数 和 的图象 (图 3.2-8), 你能发现这两个函数图象有什么共同特征吗? 你能用符号语言精确地描述这一特征吗?
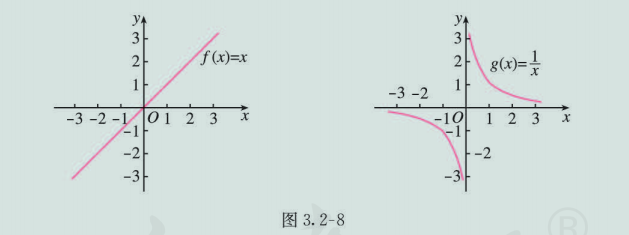
探究过程
可以发现, 两个函数的图象都关于原点成中心对称图形. 为了用符号语言描述这一特征, 不妨取自变量的一些特殊值, 看相应函数值的情况, 请完成表 3.2-2.
可以发现, 当自变量 取一对相反数时, 相应的函数值 也是一对相反数.
例如, 对于函数 , 有
实际上, , 都有 . 这时称函数 为奇函数.
一般地, 设函数 的定义域为 , 如果 , 都有 , 且 , 那么函数 就叫做奇函数 (odd function).
思考
请你仿照这个过程,说明函数 也是奇函数.
奇偶性是函数在它的定义域上的整体性质, 所以判断函数的奇偶性应先明确它的定义域。
例 6
判断下列函数的奇偶性:
(1) ;
(2) ;
(3) ;
(4) .
解:
(1) 函数 的定义域为 .
因为 , 都有 , 且
所以, 函数 为偶函数.
(2) 函数 的定义域为 .
因为 , 都有 , 且
所以, 函数 为奇函数.
(3) 函数 的定义域为 .
因为 , 都有 , 且
所以, 函数 为奇函数.
(4) 函数 的定义域为 .
因为 , 都有 , 且
所以, 函数 为偶函数.
思考
(1) 判断函数 的奇偶性.
(2) 图 3.2-9 是函数 图象的一部分, 你能根据 的奇偶性画出它在 轴左边的图象吗?
(3) 一般地, 如果知道 为偶(奇)函数, 那么我们可以怎样简化对它的研究?
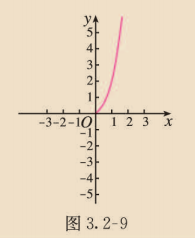
练习
1.
已知 是偶函数, 是奇函数, 试将下图补充完整.

2.
判断下列函数的奇偶性:
(1) ;
(2) .
3.
(1) 从偶函数的定义出发, 证明函数 是偶函数的充要条件是它的图象关于 轴对称;
(2) 从奇函数的定义出发, 证明函数 是奇函数的充要条件是它的图象关于原点对称.
习题 3.2
复习巩固
1.
根据下图说出函数的单调区间及在每一单调区间上的单调性.
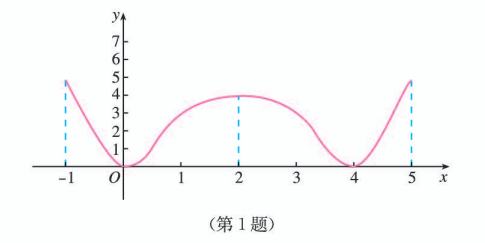
2.
画出下列函数的图像, 并根据图象说出函数 的单调区间及在每一单调区间上的单调性.
(1) ;
(2) .
3.
证明:
(1) 函数 是减函数;
(2) 函数 在 上单调递增;
(3) 函数 在 上单调递增.
4.
某汽车租凭公司的月收益 (单位: 元) 与每辆车的月租金 (单位: 元) 间的关系为 , 那么, 每辆车的月租金为多少元时, 租赁公司的月收益最大? 最大月收益是多少?
5.
判断下列函数的奇偶性:
(1) ;
(2) .
综合运用
6.
一名心率过速患者服用某种药物后心率立刻明显减慢, 之后随着药力的减退, 心率再次慢慢升高. 画出自服药那一刻起, 心率关于时间的一个可能的图象 (示意图).
7.
已知函数 ,
(1) 求 的单调区间;
(2) 求 的最小值.
8.
(1) 根据函数单调性的定义证明函数 在区间 上单调递增.
(2) 讨论函数 在区间 上的单调性.
(3) 讨论函数 在区间 上的单调性.
9.
设函数 的定义域为 , 区间 , 记 . 证明:
(1) 函数 在区间 上单调递增的充要条件是: , 都有 ;
(2) 函数 在区间 上单调递减的充要条件是: , 都有 .
10.
如图所示, 动物园要建造一面靠墙的两间面积相同的矩形熊猫居室, 如果可供建造围墙的材料总长是 , 那么宽 (单位: ) 为多少时才能使所建造的每间熊猫居室面积最大?每间熊猫居室的最大面积是多少?
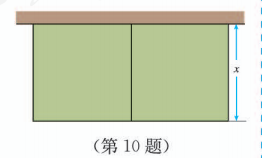
11.
已知函数 是定义域为 的奇函数,当 时, . 画出函数 的图象, 并求出函数的解析式.
拓广探索
12.
已知函数 是偶函数, 而且在 上单调递减, 判断 在 上单调递增还是单调递减, 并证明你的判断.
13.
我们知道, 函数 的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数, 有同学发现可以将其推广为: 函数 的图象关于点 成中心对称图形的充要条件是函数 为奇函数.
(1) 求函数 图象的对称中心;
(2) 类比上述推广结论, 写出 “函数 的图象关于 轴成轴对称图形的充要条件是函数 为偶函数” 的一个推广结论.
信息技术应用:用计算机绘制函数图象
用计算机绘制函数图象
利用计算机软件可以便捷、迅速地绘制各种函数图象. 不同的计算机软件绘制函数图象的具体操作不尽相同, 但都是基于我们熟悉的描点作图, 即给自变量赋值, 用计算法则算出相应的函数值, 再由这些对应值生成一系列的点, 最后连接这些点描绘出函数图象. 下面以软件《GeoGebra》为例, 介绍用计算机软件绘制函数图象的方法.
一、直接输入函数绘制函数 的图象
打开软件 《GeoGebra》, 在下方的输入框内直接输入 “ y=x^3 ”, 回车, 在代数区就会显示该函数的解析式 “ ”, 而在绘图区就会自动显示相应函数 的图象 (如图 1).
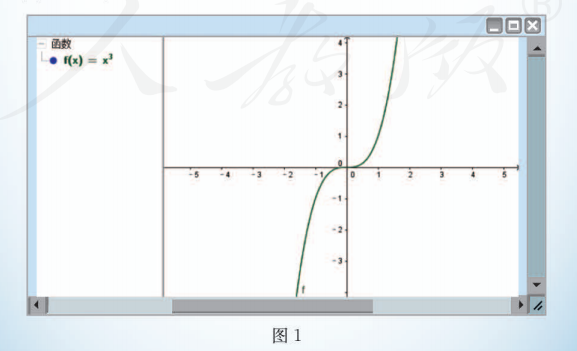
二、绘制含参数 的函数 的图象
(1) 打开软件 《GeoGebra》, 在输入框内输入参数 “ ”, 回车, 创建滑动条 , 选择 的 “属性”, 依图 2 提示可自由设置其最小值、最大值、增量等后关闭.
(2) 在输入框内直接输入函数 “ y = b * x ^ 2 ”, 回车, 在绘图区直接显示出当时参数 的值对应的函数 的图象 (图 2).
当你左右移动滑动条中点 的位置时, 函数 的图象就会 “动” 起来,如图 2.
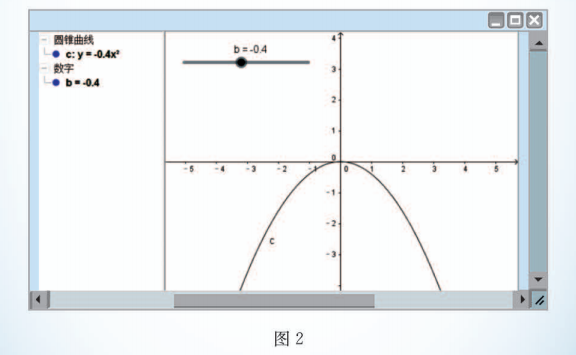
如果有条件, 请你绘制函数 的图象, 并探究系数 , 对函数图象的影响.