7.4 小结

2024-06-26 22:35:42 新建

本章知识结构

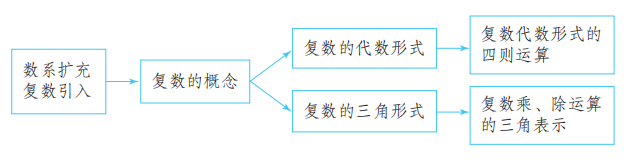
回顾与思考

本章我们通过解方程引入了复数, 进而研究了复数的表示和运算, 以及它们的几何意义, 将实数系扩充成复数系.

在数学史上, 从古希腊丢番图时代人们求一元二次方程的解时发现复数问题开始, 到意大利数学家卡尔达诺在他 1545 年出版的《大术》中, 在求解一元三次方程过程中无法回避虚数问题, 再到 18 世纪末韦塞尔给出复数的几何表示, 人们才开始接受复数, 这是一个漫长而曲折的过程, 其中充满着数学家的想象力、创造力, 表现了数学家不屈不挠、精益求精的精神. 我们看到, 人们是在解决纯粹的数学问题的过程中发现复数的, 但它现在在流体力学、信号分析等学科中得到了广泛的应用. 1843 年, 英国数学家哈密顿在复数基础上构造了四元数, 从而导致了物理学中著名的麦克斯韦方程的建立, 显示了人类理性思维的强大作用.

复数本质上是一对有序实数, 因此复数与复平面内的点是一一对应的, 与复平面内以原点为起点的向量也是一一对应的, 由复数的向量表示可以进一步得到复数的三角形式. 因此, 复数的代数形式、三角形式都具有明显的几何意义. 从复数的运算看, 复数代数形式的加、减运算的几何意义, 就是相应平面向量的加减运算; 复数的乘、除运算的几何意义, 就是平面向量的旋转、伸缩. 本章强调数与形的结合, 学习时应注意把握数形结合的思想方法.

学习本章时, 应注意复数与实数、有理数的联系, 复数及其代数形式的加法、减法、乘法运算与多项式及其加法、减法、乘法运算的联系, 应注意复数及其代数形式的加、减运算与平面向量及其加、减运算的联系, 还应关注复数的三角表示以及复数的乘、除运算与平面向量、三角函数的联系. 这些联系可以用以下框图表示:

请你带着下面的问题, 复习一下全章内容吧!

收集一些从实数系扩充到复数系的数学史料, 并对 “整数——有理数——实数——复数”的数系扩充过程进行整理.
学习复数应联系实数, 注意到复数事实上是一对有序实数, 请比较实数、虚数、纯虚数、复数之间的区别和联系, 比较实数和复数的几何意义的区别.
你对复数四则运算法则规定的合理性, 以及复数代数形式的加、减运算与向量的加、减运算的一致性有什么体会?
什么是复数的三角形式? 它与复数的几何意义之间有什么联系? 复数的代数形式与三角形式之间有什么关系?
复数乘、除运算的几何意义是什么?
比较复数乘、除运算的代数表示与三角表示, 体会复数的三角表示给乘、除运算带来的便利.

复习参考题 7

复习巩固

选择题
(1) 复数 $a + b i$ 与 $c + d i$ 的积是实数的充要条件是 ( ).
(A) $a d + b c = 0$
(B) $a c + b d = 0$
(C) $a c = b d$
(D) $a d = b c$
(2) 复数 $\frac{5}{i - 2}$ 的共轭复数是（）.
(A) $i + 2$
(B) $i - 2$
(C) $- 2 - i$
(D) $2 - i$
(3) 当 $\frac{2}{3} < m < 1$ 时，复数 $m (3 + i) - (2 + i)$ 在复平面内对应的点位于（）.
(A) 第一象限
(B) 第二象限
(C) 第三象限
(D) 第四象限
$^{*}$ (4) 复数 $sin 4 0^{\circ} - i cos 4 0^{\circ}$ 的辐角主值是 ( ).
(A) $4 0^{\circ}$
(B) $14 0^{\circ}$
(C) $22 0^{\circ}$
(D) $31 0^{\circ}$

填空题
(1) 若复数 $z$ 的模为 $5$ , 虚部为 $- 4$ , 则复数 $z =$ .
(2) 已知复数 $z = 1 - 2 i$ , 那么 $\frac{1}{z ˉ} =$ .
(3) 复数 $6 + 5 i$ 与 $- 3 + 4 i$ 分别表示向量 $O A$ 与 $OB$ , 则表示向量 $B A$ 的复数为 .
$^{*}$ (4) 如果向量 $OZ$ 对应复数 $4 i, OZ$ 绕点 $O$ 按逆时针方向旋转 $4 5^{\circ}$ 后再把模变为原来的 $2$ 倍得到向量 $O Z_{1}$ , 那么与 $O Z_{1}$ 对应的复数是 (用代数形式表示).

求证: $z \cdot \overset{z}{ˉ} = ∣ z ∣^{2} = ∣ \overset{z}{ˉ} ∣^{2}$ .

已知复数 $z$ 与 $(z + 2)^{2} - 8 i$ 都是纯虚数, 求 $z$ .

在复数集 $C$ 中解下列方程:
(1) $4 x^{2} + 9 = 0$ ;
(2) $(x - 3) (x - 5) + 2 = 0$ .

综合运用

已知 $z_{1} = 5 + 10 i, z_{2} = 3 - 4 i, \frac{1}{z} = \frac{1}{z _{1}} + \frac{1}{z _{2}}$ , 求 $z$ .

已知 $(1 + 2 i) \overset{z}{ˉ} = 4 + 3 i$ , 求 $z$ 及 $\frac{z}{z ˉ}$ .

(1) 求 $i^{1}, i^{2}, i^{3}, i^{4}, i^{5}, i^{6}, i^{7}, i^{8}$ 的值;
(2) 由 (1) 推测 $i^{n} (n \in N^{*})$ 的值有什么变化规律, 并把这个规律用式子表示出来.

拓广探索

已知复数 $z_{1} = m + (4 - m^{2}) i (m \in R), z_{2} = 2 cos θ + (λ + 3 sin θ) i (λ, θ \in R)$ , 并且 $z_{1} = z_{2}$ ,求 $λ$ 的取值范围.

$^{*}$ 10.

在复平面的上半平面内有一个菱形 $O A BC, ∠ A OC = 12 0^{\circ}$ , 点 $A$ 所对应的复数是 $2 + i$ , 求另外两个顶点 $B, C$ 所对应的复数.