5.4 三角函数的图象与性质

2024-03-28 22:12:45 新建

前面给出了三角函数的定义, 如何从定义出发研究这个函数呢? 类比已有的研究方法, 可以先画出函数图象, 通过观察图象的特征, 获得函数性质的一些结论.

我们知道, 单位圆上任意一点在圆周上旋转一周就回到原来的位置, 这一现象可以用公式

$sin (x \pm 2 π) = sin x, cos (x \pm 2 π) = cos x$

来表示. 这说明, 自变量每增加 (减少) $2 π$ , 正弦函数值、余弦函数值将重复出现. 利用这一特性, 就可以简化正弦函数、余弦函数的图象与性质的研究过程.

5.4.1 正弦函数、余弦函数的图象

下面先研究函数 $y = sin x, x \in R$ 的图象, 从画函数 $y = sin x, x \in [0, 2 π]$ 的图象开始.

思考

在 $[0, 2 π]$ 上任取一个值 $x_{0}$ , 如何利用正弦函数的定义, 确定正弦函数值 $sin x_{0}$ ,并画出点 $T (x_{0}, sin x_{0})$ ?

解

如图 5.4-1, 在直角坐标系中画出以原点 $O$ 为圆心的单位圆, $⊙ O$ 与 $x$ 轴正半轴的交点为 $A (1, 0)$ . 在单位圆上, 将点 $A$ 绕着点 $O$ 旋转 $x_{0}$ 弧度至点 $B$ , 根据正弦函数的定义, 点 $B$ 的纵坐标 $y_{0} = sin x_{0}$ . 由此, 以 $x_{0}$ 为横坐标, $y_{0}$ 为纵坐标画点, 即得到函数图象上的点 $T (x_{0}, sin x_{0})$ .

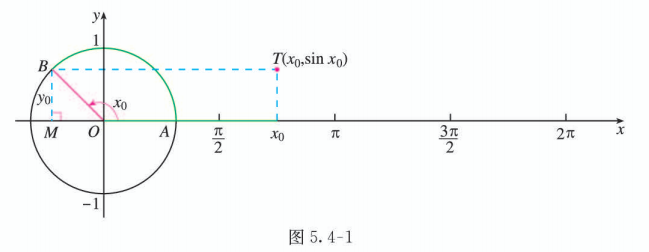
若把 $x$ 轴上从 0 到 $2 π$ 这一段分成 12 等份, 使 $x_{0}$ 的值分别为 $0, \frac{π}{6}, \frac{π}{3}, \frac{π}{2}, \dots, 2 π$ ,它们所对应的角的终边与单位圆的交点将圆周 12 等分, 再按上述画点 $T (x_{0}, sin x_{0})$ 的方法, 就可画出自变量取这些值时对应的函数图象上的点 (图 5.4-2).

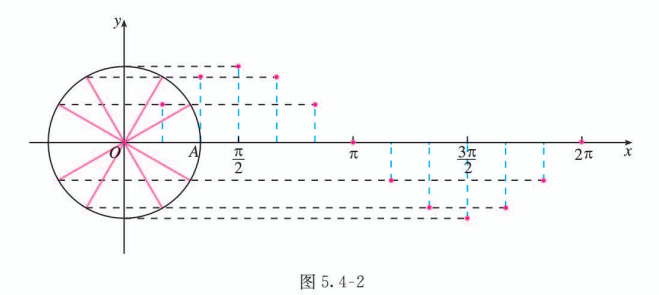
事实上，利用信息技术，可使 $x_{0}$ 在区间 $[0, 2 π]$ 上取到足够多的值而画出足够多的点 $T (x_{0}, sin x_{0})$ , 将这些点用光滑的曲线连接起来, 可得到比较精确的函数 $y = sin x, x \in$ $[0, 2 π]$ 的图象 (图 5.4-3).

思考

根据函数 $y = sin x, x \in [0, 2 π]$ 的图象, 你能想象函数 $y = sin x, x \in R$ 的图象吗?

解

由诱导公式一可知, 函数 $y = sin x, x \in [2 kπ, 2 (k + 1) π], k \in Z$ 且 $k \neq = 0$ 的图象与 $y = sin x, x \in [0, 2 π]$ 的图象形状完全一致. 因此将函数 $y = sin x, x \in [0, 2 π]$ 的图象不断向左、向右平移 (每次移动 $2 π$ 个单位长度), 就可以得到正弦函数 $y = sin x, x \in R$ 的图象 (图 5.4-4).

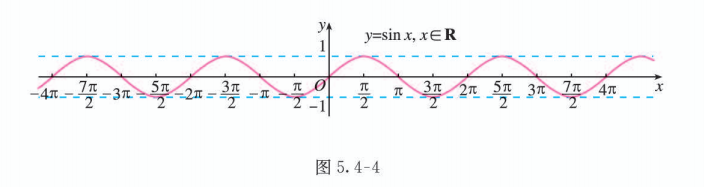
定义正弦曲线

正弦函数的图象叫做正弦曲线 (sine curve), 是一条 “波浪起伏” 的连续光滑曲线.

思考

在确定正弦函数的图象形状时, 应抓住哪些关键点?

观察图 5.4-3, 在函数 $y = sin x, x \in [0, 2 π]$ 的图象上, 以下五个点:

$(0, 0), (\frac{π}{2}, 1), (π, 0), (\frac{3 π}{2}, - 1), (2 π, 0)$

在确定图象形状时起关键作用. 描出这五个点, 函数 $y = sin x, x \in [0, 2 π]$ 的图象形状就基本确定了. 因此, 在精确度要求不高时, 常先找出这五个关键点, 再用光滑的曲线将它们连接起来, 得到正弦函数的简图. 这种近似的 “五点（画图）法” 是非常实用的.

由三角函数的定义可知, 正弦函数、余弦函数是一对密切关联的函数. 下面我们利用这种关系, 借助正弦函数的图象画出余弦函数的图象.

思考

你认为应该利用正弦函数和余弦函数的哪些关系, 通过怎样的图形变换, 才能将正弦函数的图象变换为余弦函数的图象?

解

对于函数 $y = cos x$ , 由诱导公式 $cos x = sin (x + \frac{π}{2})$ 得,

$y = cos x = sin (x + \frac{π}{2}), x \in R .$

而函数

$y = sin (x + \frac{π}{2}), x \in R$

的图象可以通过正弦函数

$y = sin x, x \in R$

的图象向左平移 $\frac{π}{2}$ 个单位长度而得到. 所以, 将正弦函数的图象向左平移 $\frac{π}{2}$ 个单位长度,就得到余弦函数的图象, 如图 5.4-5 所示.

思考

你能说明理由吗?

定义余弦曲线

余弦函数 $y = cos x, x \in R$ 的图象叫做余弦曲线 (cosine curve). 它是与正弦曲线具有相同形状的 “波浪起伏” 的连续光滑曲线.

探究

类似于用 “五点法” 画正弦函数图象, 找出余弦函数在区间 $[- π, π]$ 上相应的五个关键点, 将它们的坐标填入表 5.4-1, 然后画出 $y = cos x, x \in [- π, π]$ 的简图.

例 1

画出下列函数的简图:
(1) $y = 1 + sin x, x \in [0, 2 π]$ ;
(2) $y = - cos x, x \in [0, 2 π]$ .

解：

(1) 按五个关键点列表:

$x$	0	$\frac{π}{2}$	$π$	$\frac{3 π}{2}$	$2 π$
$sin x$	0	1	0	-1	0
$1 + sin x$	1	2	1	0	1

描点并将它们用光滑的曲线连接起来 (图 5.4-6):

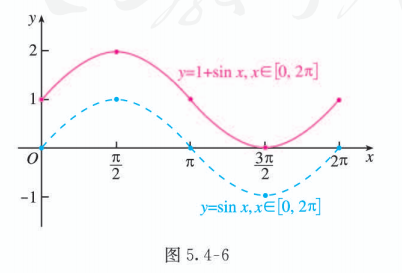
(2) 按五个关键点列表:

$x$	0	$\frac{π}{2}$	$π$	$\frac{3 π}{2}$	$2 π$
$cos x$	1	0	-1	0	1
$- cos x$	-1	0	1	0	-1

描点并将它们用光滑的曲线连接起来（图 5.4-7):

思考

你能利用函数 $y = sin x, x \in [0, 2 π]$ 的图象, 通过图象变换得到 $y = 1 + sin x$ , $x \in [0, 2 π]$ 的图象吗? 同样地, 利用函数 $y = cos x, x \in [0, 2 π]$ 的图象, 通过怎样的图象变换就能得到函数 $y = - cos x, x \in [0, 2 π]$ 的图象?

练习

在同一直角坐标系中, 画出函数

$y = sin x, x \in [0, 2 π], y = cos x, x \in [- \frac{π}{2}, \frac{3 π}{2}]$

的图象. 通过观察两条曲线, 说出它们的异同.

用五点法分别画下列函数在 $[- π, π]$ 上的图象:
(1) $y = - sin x$ ;
(2) $y = 2 - cos x$ .

想一想函数 $y = ∣ sin x ∣$ 与 $y = sin x$ 的图象及其关系, 并借助信息技术画出函数的图象进行检验.

(多项选择题) 函数 $y = 1 + cos x, x \in (\frac{π}{3}, 2 π)$ 的图象与直线 $y = t$ ( $t$ 为常数) 的交点可能有 ().
(A) 0 个
(B) 1 个
(C) 2 个
(D) 3 个
(E) 4 个

5.4.2 正弦函数、余弦函数的性质

探究

类比以往对函数性质的研究, 你认为应研究正弦函数、余弦函数的哪些性质? 观察它们的图象, 你能发现它们具有哪些性质?

根据研究函数的经验, 我们要研究正弦函数、余弦函数的单调性、奇偶性、最大 (小) 值等. 另外, 三角函数是刻画 “周而复始” 现象的数学模型, 与此对应的性质是特别而重要的.

1. 周期性

定理周期性

观察正弦函数的图象, 可以发现, 在图象上, 横坐标每隔 $2 π$ 个单位长度, 就会出现纵坐标相同的点, 这就是正弦函数值具有的 “周而复始” 的变化规律. 实际上, 这一点既可从定义中看出, 也能从诱导公式 $sin (x + 2 kπ) = sin x (k \in Z)$ 中得到反映, 即自变量 $x$ 的值增加 $2 π$ 整数倍时所对应的函数值, 与 $x$ 所对应的函数值相等. 数学上, 用周期性这个概念来定量地刻画这种 “周而复始” 的变化规律.

定义周期函数，周期

一般地, 设函数 $f (x)$ 的定义域为 $D$ , 如果存在一个非零常数 $T$ , 使得对每一个 $x \in D$ 都有 $x + T \in D$ , 且

$f (x + T) = f (x),$

那么函数 $f (x)$ 就叫做周期函数（periodic function). 非零常数 $T$ 叫做这个函数的周期（period).

定理周期函数的周期不止一个.

周期函数的周期不止一个. 例如, $2 π, 4 π, 6 π, \dots$ 以及 $- 2 π, - 4 π, - 6 π, \dots$ 都是正弦函数的周期. 事实上, $\forall k \in Z$ 且 $k \neq = 0$ , 常数 $2 kπ$ 都是它的周期.

定义最小正周期

如果在周期函数 $f (x)$ 的所有周期中存在一个最小的正数, 那么这个最小正数就叫做 $f (x)$ 的最小正周期.

定理

根据上述定义, 我们有:

正弦函数是周期函数, $2 kπ (k \in Z$ 且 $k \neq = 0)$ 都是它的周期, 最小正周期是 $2 π$ .

类似地, 余弦函数也是周期函数, $2 kπ (k \in Z$ 且 $k \neq = 0)$ 都是它的周期, 最小正周期是 $2 π$ . $^{[1]}$

[1] 证明从略. 同学们可以从函数图象上观察出这一结论. 今后本书中所涉及的周期，如果不加特别说明，一般都是指函数的最小正周期.

例 2

求下列函数的周期:
(1) $y = 3 sin x, x \in R$ ;
(2) $y = cos 2 x, x \in R$ ;
(3) $y = 2 sin (\frac{1}{2} x - \frac{π}{6}), x \in R$ .

分析:

通常可以利用三角函数的周期性, 通过代数变形, 得出等式 $f (x + T) = f (x)$ 而求出相应的周期.
对于 (2), 应从余弦函数的周期性出发, 通过代数变形得出 $cos 2 (x + T) = cos 2 x, x \in R$ ;
对于 (3), 应从正弦函数的周期性出发, 通过代数变形得出 $sin [\frac{1}{2} (x + T) - \frac{π}{6}] =$ $sin (\frac{1}{2} x - \frac{π}{6}), x \in R$ .

解:

(1) $\forall x \in R$ , 有

$3 sin (x + 2 π) = 3 sin x .$

由周期函数的定义可知, 原函数的周期为 $2 π$ .
(2) 令 $z = 2 x$ , 由 $x \in R$ 得 $z \in R$ , 且 $y = cos z$ 的周期为 $2 π$ , 即

$cos (z + 2 π) = cos z,$

于是

$cos (2 x + 2 π) = cos 2 x,$

所以

$cos 2 (x + π) = cos 2 x, x \in R .$

由周期函数的定义可知, 原函数的周期为 $π$ .
(3) 令 $z = \frac{1}{2} x - \frac{π}{6}$ , 由 $x \in R$ 得 $z \in R$ , 且 $y = 2 sin z$ 的周期为 $2 π$ , 即

$2 sin (z + 2 π) = 2 sin z,$

于是

$2 sin (\frac{1}{2} x - \frac{π}{6} + 2 π) = 2 sin (\frac{1}{2} x - \frac{π}{6}),$

所以

$2 sin [\frac{1}{2} (x + 4 π) - \frac{π}{6}] = 2 sin (\frac{1}{2} x - \frac{π}{6}) .$

由周期函数的定义可知, 原函数的周期为 $4 π$ .

思考

回顾例 2 的解答过程, 你能发现这些函数的周期与解析式中哪些量有关吗?

2. 奇偶性

定理

观察正弦曲线和余弦曲线, 可以看到正弦曲线关于原点 $O$ 对称, 余弦曲线关于 $y$ 轴对称. 这个事实, 也可由诱导公式

$sin (- x) = - sin x, cos (- x) = cos x$

得到. 所以

正弦函数是奇函数, 余弦函数是偶函数.

思考

知道一个函数具有周期性和奇偶性, 对研究它的图象与性质有什么帮助?

练习

等式 $sin (\frac{π}{6} + \frac{2}{3} π) = sin \frac{π}{6}$ 是否成立? 如果这个等式成立, 能否说 $\frac{2}{3} π$ 是正弦函数 $y = sin x, x \in R$ 的一个周期? 为什么?

求下列函数的周期, 并借助信息技术画出下列函数的图象进行检验:
(1) $y = sin \frac{3}{4} x, x \in R$ ;
(2) $y = cos 4 x, x \in R$ ;
(3) $y = \frac{1}{2} cos (2 x - \frac{π}{3}), x \in R$ ;
(4) $y = sin (\frac{1}{3} x + \frac{π}{4}), x \in R$ .

下列函数中, 哪些是奇函数? 哪些是偶函数?
(1) $y = 2 sin x$ ;
(2) $y = 1 - cos x$ ;
(3) $y = x + sin x$ ;
(4) $y = - sin x cos x$ .

设函数 $f (x) (x \in R)$ 是以 2 为最小正周期的周期函数, 且当 $x \in [0, 2]$ 时, $f (x) = (x - 1)^{2}$ . 求 $f (3), f (\frac{7}{2})$ 的值.

探究与发现

函数 $y = A sin (ω x + φ)$ 及函数 $y = A cos (ω x + φ)$ 的周期

从前面的例子中可以看出, 函数

$y = A sin (ω x + φ), x \in R$

及函数

$y = A cos (ω x + φ), x \in R$

（其中 $A, ω, φ$ 为常数, 且 $A \neq = 0, ω > 0$ ) 的周期仅与自变量的系数有关. 那么,如何用自变量的系数表示上述函数的周期呢?

事实上, 令 $z = ω x + φ$ , 那么由 $x \in R$ 得 $z \in R$ , 且函数 $y = A sin z, z \in R$ 及函数 $y = A cos z, z \in R$ 的周期都是 $2 π$ .
因为

$z + 2 π = (ω x + φ) + 2 π = ω (x + \frac{2 π}{ω}) + φ,$

所以, 自变量 $x$ 增加 $\frac{2 π}{ω}$ , 函数值就重复出现; 并且增加量小于 $\frac{2 π}{ω}$ 时, 函数值不会重复出现. 即

$T = \frac{2 π}{ω}$

是使等式

$A sin [ω (x + T) + φ] = A sin (ω x + φ), A cos [ω (x + T) + φ] = A cos (ω x + φ)$

成立的最小正数. 从而, 函数

$y = A sin (ω x + φ), x \in R$

及函数

$y = A cos (ω x + φ), x \in R$

的周期 $T = \frac{2 π}{ω}$ .

根据这个结论, 我们可以由这类函数的解析式直接写出函数的周期.

思考

想一想：上述求函数 $y = A sin (ω x + φ), x \in R$ 及函数 $y = A cos (ω x + φ)$ , $x \in R$ 周期的方法是否能推广到求一般周期函数的周期? 即命题 “如果函数 $y =$ $f (x)$ 的周期是 $T$ , 那么函数 $y = f (ω x) （ ω > 0)$ 的周期是 $\frac{T}{ω}$ ” 是否成立?

3. 单调性

根据三角函数的周期性, 只要把握了它一个周期内的规律, 就把握了整个三角函数的规律.

根据正弦函数的周期性, 我们可以先在它的一个周期的区间（如 $[- \frac{π}{2}, \frac{3 π}{2}]$ ) 上讨论它的单调性, 再利用它的周期性, 将单调性扩展到整个定义域.

观察图 5.4-8, 可以看到:

当 $x$ 由 $- \frac{π}{2}$ 增大到 $\frac{π}{2}$ 时, 曲线逐渐上升, $sin x$ 的值由 -1 增大到 1 ; 当 $x$ 由 $\frac{π}{2}$ 增大到 $\frac{3 π}{2}$ 时, 曲线逐渐下降, $sin x$ 的值由 1 减小到 -1 .

$sin x$ 的值的变化情况如表 5.4-2 所示:

这就是说,
正弦函数 $y = sin x$ 在区间 $[- \frac{π}{2}, \frac{π}{2}]$ 上单调递增, 在区间 $[\frac{π}{2}, \frac{3 π}{2}]$ 上单调递减.

由正弦函数的周期性可得,

定理正弦函数单调性

正弦函数在每一个闭区间 $[- \frac{π}{2} + 2 kπ, \frac{π}{2} + 2 kπ] (k \in Z)$ 上都单调递增, 其值从 -1 增大到 1 ; 在每一个闭区间 $[\frac{π}{2} + 2 kπ, \frac{3 π}{2} + 2 kπ] (k \in Z)$ 上都单调递减, 其值从 1 减小到 -1 .

探究

类似地, 观察余弦函数在一个周期区间 (如 $[- π, π]$ ) 上函数值的变化规律, 将看到的函数值的变化情况填人表 5.4-3:

由此可得,
函数 $y = cos x, x \in [- π, π]$ 在区间上单调递增, 其值从 -1 增大到 1 ;在区间上单调递减, 其值从 1 减小到 -1 .

由余弦函数的周期性可得，

定理余弦函数单调性

余弦函数在每一个闭区间上都单调递增, 其值从 -1 增大到 1 ; 在每一个闭区间上都单调递减, 其值从 1 减小到 -1 .

4. 最大值与最小值

从上述对正弦函数、余弦函数的单调性的讨论中容易得到,

定理正余弦函数的最值

正弦函数当且仅当 $x =$ 时取得最大值 1 , 当且仅当 $x =$ 时取得最小值 -1 ;
余弦函数当且仅当 $x =$ 时取得最大值 1 , 当且仅当 $x =$ 时取得最小值 -1 .

例 3

下列函数有最大值、最小值吗? 如果有, 请写出取最大值、最小值时自变量 $x$ 的集合, 并求出最大值、最小值.
(1) $y = cos x + 1, x \in R$ ;
(2) $y = - 3 sin 2 x, x \in R$ .

解:

容易知道, 这两个函数都有最大值、最小值.
(1) 使函数 $y = cos x + 1, x \in R$ 取得最大值的 $x$ 的集合, 就是使函数 $y = cos x$ , $x \in R$ 取得最大值的 $x$ 的集合

${x ∣ x = 2 kπ, k \in Z};$

使函数 $y = cos x + 1, x \in R$ 取得最小值的 $x$ 的集合, 就是使函数 $y = cos x, x \in R$ 取得最小值的 $x$ 的集合

${x ∣ x = (2 k + 1) π, k \in Z} .$

函数 $y = cos x + 1, x \in R$ 的最大值是 $1 + 1 = 2$ ; 最小值是 $- 1 + 1 = 0$ .

(2) 令 $z = 2 x$ , 使函数 $y = - 3 sin z, z \in R$ 取得最大值的 $z$ 的集合, 就是使 $y = sin z$ , $z \in R$ 取得最小值的 $z$ 的集合

${z ∣ ∣ z = - \frac{π}{2} + 2 kπ, k \in Z} .$

由 $2 x = z = - \frac{π}{2} + 2 kπ$ , 得 $x = - \frac{π}{4} + kπ$ . 所以, 使函数 $y = - 3 sin 2 x, x \in R$ 取得最大值的 $x$ 的集合是

${x ∣ ∣ x = - \frac{π}{4} + kπ, k \in Z} .$

同理, 使函数 $y = - 3 sin 2 x, x \in R$ 取得最小值的 $x$ 的集合是

${x ∣ ∣ x = \frac{π}{4} + kπ, k \in Z} .$

函数 $y = - 3 sin 2 x, x \in R$ 的最大值是 3 , 最小值是 -3 .

例 4

不通过求值, 比较下列各组数的大小:
(1) $sin (- \frac{π}{18})$ 与 $sin (- \frac{π}{10})$ ;
(2) $cos (- \frac{23 π}{5})$ 与 $cos (- \frac{17 π}{4})$ .

分析:

可利用三角函数的单调性比较两个同名三角函数值的大小. 为此, 先用诱导公式将已知角化为同一单调区间内的角, 然后再比较大小.

解:

(1) 因为

$- \frac{π}{2} < - \frac{π}{10} < - \frac{π}{18} < 0,$

正弦函数 $y = sin x$ 在区间 $[- \frac{π}{2}, 0]$ 上单调递增,所以

$sin (- \frac{π}{18}) > sin (- \frac{π}{10}) .$

(2)

$cos (- \frac{23 π}{5}) = cos \frac{23 π}{5} = cos \frac{3 π}{5}, cos (- \frac{17 π}{4}) = cos \frac{17 π}{4} = cos \frac{π}{4} .$

因为 $0 < \frac{π}{4} < \frac{3 π}{5} < π$ , 且函数 $y = cos x$ 在区间 $[0, π]$ 上单调递减, 所以

$cos \frac{π}{4} > cos \frac{3 π}{5},$

即

$cos (- \frac{17 π}{4}) > cos (- \frac{23 π}{5}) .$

思考

你能借助单位圆直观地比较上述两对函数值的大小吗? 试一试.

例 5

求函数 $y = sin (\frac{1}{2} x + \frac{π}{3}), x \in [- 2 π, 2 π]$ 的单调递增区间.

分析:

令 $z = \frac{1}{2} x + \frac{π}{3}, x \in [- 2 π, 2 π]$ , 当自变量 $x$ 的值增大时, $z$ 的值也随之增大, 因此若函数 $y = sin z$ 在某个区间上单调递增, 则函数 $y = sin (\frac{1}{2} x + \frac{π}{3})$ 在相应的区间上也一定单调递增.

解:

令 $z = \frac{1}{2} x + \frac{π}{3}, x \in [- 2 π, 2 π]$ , 则 $z \in [- \frac{2}{3} π, \frac{4}{3} π]$ .

因为 $y = sin z, z \in [- \frac{2 π}{3}, \frac{4 π}{3}]$ 的单调递增区间是 $[- \frac{π}{2}, \frac{π}{2}]$ , 且由

$- \frac{π}{2} ⩽ \frac{1}{2} x + \frac{π}{3} ⩽ \frac{π}{2},$

得 $- \frac{5 π}{3} ⩽ x ⩽ \frac{π}{3}$ .

所以, 函数 $y = sin (\frac{1}{2} x + \frac{π}{3}), x \in [- 2 π, 2 π]$ 的单调递增区间是 $[- \frac{5 π}{3}, \frac{π}{3}]$ .

思考

你能求出函数 $y = sin (- \frac{1}{2} x + \frac{π}{3}), x \in [- 2 π, 2 π]$ 的单调递增区间吗?

练习

观察正弦曲线和余弦曲线, 写出满足下列条件的 $x$ 所在的区间:
(1) $sin x > 0$ ;
(2) $sin x < 0$ ;
(3) $cos x > 0$ ;
(4) $cos x < 0$ .

求使下列函数取得最大值、最小值的自变量的集合, 并求出最大值、最小值.
(1) $y = 2 sin x, x \in R$ ;
(2) $y = 2 - cos \frac{x}{3}, x \in R$ .

下列关于函数 $y = 4 sin x, x \in [0, 2 π]$ 的单调性的叙述, 正确的是 ( ).
(A) 在 $[0, π]$ 上单调递增, 在 $[π, 2 π]$ 上单调递减
(B) 在 $[0, \frac{π}{2}]$ 上单调递增, 在 $[\frac{3 π}{2}, 2 π]$ 上单调递减
(C) 在 $[0, \frac{π}{2}]$ 及 $[\frac{3 π}{2}, 2 π]$ 上单调递增, 在 $[\frac{π}{2}, \frac{3 π}{2}]$ 上单调递减
(D) 在 $[\frac{π}{2}, \frac{3 π}{2}]$ 上单调递增, 在 $[0, \frac{π}{2}]$ 及 $[\frac{3 π}{2}, 2 π]$ 上单调递减

不通过求值, 比较下列各组中两个三角函数值的大小:
(1) $cos \frac{2}{7} π$ 与 $cos (- \frac{3 π}{5})$ ;
(2) $sin 25 0^{\circ}$ 与 $sin 26 0^{\circ}$ .

求函数 $y = 3 sin (2 x + \frac{π}{4}), x \in [0, π]$ 的单调递减区间.

探究与发现

利用单位圆的性质研究正弦函数、余弦函数的性质

根据三角函数的定义可知, “单位圆上点的坐标就是三角函数”. 因此, 单位圆的性质与三角函数的性质有天然的联系, 单位圆是研究三角函数性质的好工具.例如, 借助单位圆的对称性可以方便地得到诱导公式. 借助单位圆研究三角函数的性质体现了数形结合的思想方法, 有利于从整体上把握三角函数.

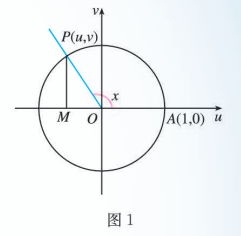
如图 1, 在直角坐标系 $u O v$ 中, 角 $x$ 的顶点与原点重合, 始边与 $O u$ 轴重合, 终边与单位圆交于点 $P (cos x, sin x)$ . 容易发现, 当角 $x$ 的终边绕原点从 $O u$ 轴的正半轴开始, 按照逆时针方向旋转时,点 $P$ 的横坐标按照

$1 \to 0 \to - 1 \to 0 \to 1 \dots$

的规律连续地、周而复始地变化; 同时, 纵坐标按照

$0 \to 1 \to 0 \to - 1 \to 0 \dots$

的规律连续地、周而复始地变化.

由上述变化规律, 可得余弦函数、正弦函数的各种性质（下述表格中的 $k \in Z$ ).

(1) 周期性
自变量每增加 $2 π$ (角 $x$ 的终边旋转一周), 余弦函数值、正弦函数值重复出现，所以余弦函数、正弦函数的周期都是 $2 π$ .

(2) 奇偶性
角 $x$ 、角 $- x$ 与单位圆的交点 $P (cos x, sin x) 、 P^{'} (cos (- x), sin (- x))$ 关于 $O u$ 轴对称, 所以 $cos (- x) = cos x, sin (- x) = - sin x$ , 所以余弦函数为偶函数, 正弦函数为奇函数.

(3) 单调性
余弦函数的单调性:

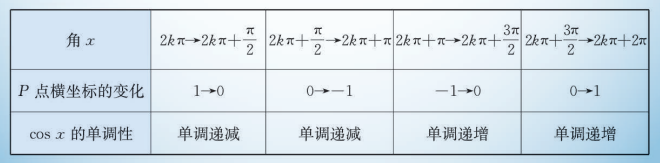
正弦函数的单调性：

(4) 最大值、最小值

余弦函数的最大值、最小值:

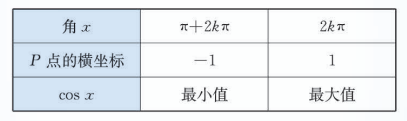
正弦函数的最大值、最小值:

在后续的学习中我们还可以看到, 借助单位圆的性质 (主要是对称性), 不仅可以得到三角函数的各种性质, 而且可以推导各种三角公式.

5.4.3 正切函数的性质与图象

思考

(1) 根据研究正弦函数、余弦函数的经验, 你认为应如何研究正切函数的图象与性质?
(2) 你能用不同的方法研究正切函数吗?
有了前面的知识准备, 我们可以换个角度, 即从正切函数的定义出发研究它的性质,再利用性质研究正切函数的图象.

定理 1. 周期性

由诱导公式

$tan (x + π) = tan x, x \in R, 且 x \neq = \frac{π}{2} + kπ, k \in Z$

可知, 正切函数是周期函数, 周期是 $π$ .

定理 2. 奇偶性

由诱导公式

$tan (- x) = - tan x, x \in R, 且 x \neq = \frac{π}{2} + kπ, k \in Z$

可知, 正切函数是奇函数.

思考

你认为正切函数的周期性和奇偶性对研究它的图象及其他性质会有什么帮助?

答

可以先考察函数 $y = tan x, x \in [0, \frac{π}{2})$ 的图象与性质, 然后再根据奇偶性、周期性进行拓展.

探究

如何画出函数 $y = tan x, x \in [0, \frac{π}{2})$ 的图象?

答

如图 5.4-9, 设 $x \in [0, \frac{π}{2})$ , 在直角坐标系中画出角 $x$ 的终边与单位圆的交点 $B (x_{0}, y_{0})$ . 过点 $B$ 作 $x$ 轴的垂线, 垂足为 $M$ ; 过点 $A (1, 0)$ 作 $x$ 轴的垂线与角 $x$ 的终边交于点 $T$ , 则

$tan x = \frac{y _{0}}{x _{0}} = \frac{MB}{OM} = \frac{A T}{O A} = A T .$

由此可见, 当 $x \in [0, \frac{π}{2})$ 时, 线段 $A T$ 的长度就是相应角 $x$ 的正切值. 我们可以利用线段 $A T$ 画出函数 $y = tan x, x \in$ $[0, \frac{π}{2})$ 的图象, 如图 5.4-10 所示.

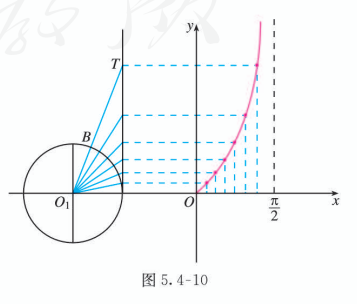
观察图 5.4-10 可知, 当 $x \in [0, \frac{π}{2})$ 时, 随着 $x$ 的增大, 线段 $A T$ 的长度也在增大, 而且当 $x$ 趋向于 $\frac{π}{2}$ 时, $A T$ 的长度趋向于无穷大. 相应地, 函数 $y = tan x, x \in [0, \frac{π}{2})$ 的图象从左向右呈不断上升趋势,且向右上方无限逼近直线 $x = \frac{π}{2}$ .

探究

你能借助以上结论, 并根据正切函数的性质, 画出正切函数的图象吗? 正切函数的图象有怎样的特征?

答

根据正切函数是奇函数, 只要画 $y = tan x, x \in [0, \frac{π}{2})$ 的图象关于原点的对称图形,就可得到 $y = tan x, x \in (- \frac{π}{2}, 0]$ 的图象; 根据正切函数的周期性, 只要把函数 $y =$ $tan x, x \in (- \frac{π}{2}, \frac{π}{2})$ 的图象向左、右平移, 每次平移 $π$ 个单位, 就可得到正切函数

$y = tan x, x \in R, x \neq = \frac{π}{2} + kπ, k \in Z$

的图象,

定义正切曲线

我们把它叫做正切曲线 (tangent curve) (图 5.4-11).

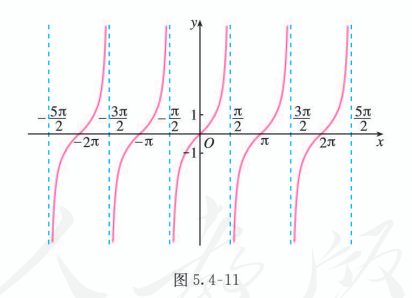
从图 5.4-11 可以看出, 正切曲线是被与 $y$ 轴平行的一系列直线 $x = \frac{π}{2} + kπ, k \in Z$ 所隔开的无穷多支形状相同的曲线组成的.

定理 3. 单调性

观察正切曲线可知, 正切函数在区间 $(- \frac{π}{2}, \frac{π}{2})$ 上单调递增.

由正切函数的周期性可得,

正切函数在每一个区间 $(- \frac{π}{2} + kπ, \frac{π}{2} + kπ) (k \in Z)$ 上都单调递增.

定理 4. 值域

当 $x \in (- \frac{π}{2}, \frac{π}{2})$ 时, $tan x$ 在 $(- \infty, + \infty)$ 内可取到任意实数值, 但没有最大值、最小值.

因此, 正切函数的值域是实数集 $R$ .

例 6

求函数 $y = tan (\frac{π}{2} x + \frac{π}{3})$ 的定义域、周期及单调区间.

分析：

利用正切函数的性质，通过代数变形可以得出相应的结论.

解:

自变量 $x$ 的取值应满足

$\frac{π}{2} x + \frac{π}{3} \neq = kπ + \frac{π}{2}, k \in Z,$

即

$x \neq = 2 k + \frac{1}{3}, k \in Z .$

所以, 函数的定义域是 ${x ∣ ∣ x \neq = 2 k + \frac{1}{3}, k \in Z}$ .

设 $z = \frac{π}{2} x + \frac{π}{3}$ , 又 $tan (z + π) = tan z ，$
所以

$tan [(\frac{π}{2} x + \frac{π}{3}) + π] = tan (\frac{π}{2} x + \frac{π}{3}),$

即

$tan [\frac{π}{2} (x + 2) + \frac{π}{3}] = tan (\frac{π}{2} x + \frac{π}{3}) .$

因为 $\forall x \in {x ∣ ∣ x \neq = 2 k + \frac{1}{3}, k \in Z}$ 都有

$tan [\frac{π}{2} (x + 2) + \frac{π}{3}] = tan (\frac{π}{2} x + \frac{π}{3}),$

所以，函数的周期为 2 .

由 $- \frac{π}{2} + kπ < \frac{π}{2} x + \frac{π}{3} < \frac{π}{2} + kπ, k \in Z$ 解得

$- \frac{5}{3} + 2 k < x < \frac{1}{3} + 2 k, k \in Z .$

因此, 函数的单调递增区间为 $(- \frac{5}{3} + 2 k, \frac{1}{3} + 2 k), k \in Z$ .

练习

借助函数 $y = tan x$ 的图象解不等式 $tan x ⩾ - 1, x \in [0, \frac{π}{2}) \cup (\frac{π}{2}, π)$ .

观察正切曲线, 写出满足下列条件的 $x$ 值的范围:
(1) $tan x > 0$ ;
(2) $tan x = 0$ ;
(3) $tan x < 0$ .

求函数 $y = tan 3 x$ 的定义域.

求下列函数的周期:
(1) $y = tan 2 x, x \neq = \frac{π}{4} + \frac{kπ}{2} (k \in Z)$ ;
(2) $y = 5 tan \frac{x}{2}, x \neq = (2 k + 1) π (k \in Z)$ .

不通过求值, 比较下列各组中两个正切值的大小:
(1) $tan (- 5 2^{\circ})$ 与 $tan (- 4 7^{\circ})$ ;
(2) $tan \frac{13 π}{4}$ 与 $tan \frac{17 π}{5}$ .

习题 5.4

复习巩固

画出下列函数的简图:
(1) $y = 1 - sin x, x \in [0, 2 π]$ ;
(2) $y = 3 cos x + 1, x \in [0, 2 π]$ .

求下列函数的周期:
(1) $y = sin \frac{2}{3} x, x \in R$ ;
(2) $y = \frac{1}{2} cos 4 x, x \in R$ .

下列函数中, 哪些是奇函数? 哪些是偶函数? 哪些既不是奇函数, 也不是偶函数?
(1) $y = ∣ sin x ∣$ ;
(2) $y = 1 - cos 2 x$ ;
(3) $y = - 3 sin 2 x$ ;
(4) $y = 1 + 2 tan x$ .

求使下列函数取得最大值、最小值的自变量 $x$ 的集合, 并求出最大值、最小值:
(1) $y = 1 - \frac{1}{2} cos \frac{π}{3} x, x \in R$ ;
(2) $y = 3 sin (2 x + \frac{π}{4}), x \in R$ ;
(3) $y = - \frac{3}{2} cos (\frac{1}{2} x - \frac{π}{6}), x \in R$ ;
(4) $y = \frac{1}{2} sin (\frac{1}{2} x + \frac{π}{3}), x \in R$ .

利用函数的单调性比较下列各组中两个三角函数值的大小:
(1) $sin 10 3^{\circ} 1 5^{'}$ 与 $sin 16 4^{\circ} 3 0^{'}$ ;
(2) $cos (- \frac{3}{10} π)$ 与 $cos (- \frac{4}{9} π)$ ;
(3) $sin 50 8^{\circ}$ 与 $sin 14 4^{\circ}$ ;
(4) $cos (\frac{47}{10} π)$ 与 $cos (\frac{44}{9} π)$ .

求下列函数的单调区间:
(1) $y = 1 + sin x, x \in [0, 2 π]$ ;
(2) $y = - cos x, x \in [0, 2 π]$ .

求函数 $y = - tan (x + \frac{π}{6}) + 2$ 的定义域.

求函数 $y = tan (2 x - \frac{π}{3}), x \neq = \frac{5 π}{12} + \frac{kπ}{2} (k \in Z)$ 的周期.

利用正切函数的单调性比较下列各组中两个函数值的大小:
(1) $tan (- \frac{π}{5})$ 与 $tan (- \frac{3 π}{7})$ ;
(2) $tan 151 9^{\circ}$ 与 $tan 149 3^{\circ}$ ;
(3) $tan 6 \frac{9}{11} π$ 与 $tan (- 5 \frac{3}{11} π)$ ;
(4) $tan \frac{7 π}{8}$ 与 $tan \frac{π}{6}$ .

综合运用

10.

求下列函数的值域:
(1) $y = sin x, x \in [\frac{π}{4}, \frac{5 π}{4}]$ ;
(2) $y = cos (x + \frac{π}{3}), x \in [0, \frac{π}{2}]$ .

11.

根据正弦函数、余弦函数的图象, 写出使下列不等式成立的 $x$ 的取值集合:
(1) $sin x ⩾ \frac{3}{2} (x \in R)$ ;
(2) $2 + 2 cos x ⩾ 0 (x \in R)$ .

12.

下列四个函数中, 以 $π$ 为最小正周期, 且在区间 $(\frac{π}{2}, π)$ 上单调递减的是 ( ).
(A) $y = ∣ sin x ∣$
(B) $y = cos x$
(C) $y = tan x$
(D) $y = cos \frac{x}{2}$

13.

若 $x$ 是斜三角形的一个内角, 写出使下列不等式成立的 $x$ 的集合:
(1) $1 + tan x ⩽ 0$ ;
(2) $tan x - 3 ⩾ 0$ .

14.

求函数 $y = - tan (2 x - \frac{3 π}{4})$ 的单调区间.

15.

已知函数 $y = f (x)$ 是定义在 $R$ 上周期为 2 的奇函数, 若 $f (0.5) = 1$ , 求 $f (1), f (3.5)$ 的值.

16.

已知函数 $f (x) = \frac{1}{2} sin (2 x - \frac{π}{3}), x \in R$ ,
(1) 求 $f (x)$ 的最小正周期;
(2) 求 $f (x)$ 在区间 $[- \frac{π}{4}, \frac{π}{4}]$ 上的最大值和最小值.

拓广探索

17.

在直角坐标系中, 已知 $⊙ O$ 是以原点 $O$ 为圆心, 半径长为 2 的圆, 角 $x (rad)$ 的终边与 $⊙ O$ 的交点为 $B$ , 求点 $B$ 的纵坐标 $y$ 关于 $x$ 的函数解析式, 并借助信息技术画出其图象.

18.

已知函数 $y = f (x) (x \in R)$ 是周期函数, 周期为 2 , 其部分图象如图所示,
(1) 写出函数 $y = f (x)$ 的解析式;
(2) 画出函数 $y = f (x + 1)$ 的图象.

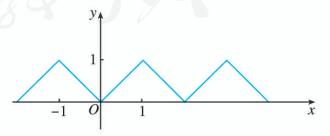
19.

容易知道, 正弦函数 $y = sin x$ 是奇函数,正弦曲线关于原点对称, 即原点是正弦曲线的对称中心. 除原点外, 正弦曲线还有其他对称中心吗? 如果有, 那么对称中心的坐标是什么? 另外, 正弦曲线是轴对称图形吗? 如果是, 那么对称轴的方程是什么? 你能用已经学过的正弦函数性质解释上述现象吗? 对余弦函数和正切函数, 讨论上述同样的问题.