4.1 指数

2024-02-08 22:08:39 新建

为了研究指数函数, 我们需要把指数的范围拓展到全体实数.

初中已经学过整数指数幂. 在学习幂函数时, 我们把正方形场地的边长 $c$ 关于面积 $S$ 的函数 $c = S$ 记作 $c = S^{\frac{1}{2}}$ . 像 $S^{\frac{1}{2}}$ 这样以分数为指数的幂, 其意义是什么呢? 下面从已知的平方根、立方根的意义入手展开研究.

4.1.1 n 次方根与分数指数幂

例子

我们知道:
如果 $x^{2} = a$ , 那么 $x$ 叫做 $a$ 的平方根. 例如, $\pm 2$ 就是 4 的平方根.
如果 $x^{3} = a$ , 那么 $x$ 叫做 $a$ 的立方根. 例如, 2 就是 8 的立方根.
类似地, 由于 $(\pm 2)^{4} = 16$ , 我们把 $\pm 2$ 叫做 $16$ 的 $4$ 次方根; 由于 $2^{5} = 32$ , $2$ 叫做 $32$ 的 $5$ 次方根.

定义 $n$ 次方根

一般地, 如果 $x^{n} = a$ , 那么 $x$ 叫做 $a$ 的 $n$ 次方根, 其中 $n > 1$ , 且 $n \in N^{*}$ .

当 $n$ 是奇数时, 正数的 $n$ 次方根是一个正数, 负数的 $n$ 次方根是一个负数. 这时, $a$ 的 $n$ 次方根用符号 $n a$ 表示. 例如,

$532 = 2, 5 - 32 = - 2, 3 a^{6} = a^{2} .$

当 $n$ 是偶数时, 正数的 $n$ 次方根有两个, 这两个数互为相反数. 这时, 正数 $a$ 的正的 $n$ 次方根用符号 $n a$ 表示, 负的 $n$ 次方根用符号 $- n a$ 表示. 正的 $n$ 次方根与负的 $n$ 次方根可以合并写成 $\pm n a (a > 0)$ . 例如，

$416 = 2, - 416 = - 2, \pm 416 = \pm 2 .$

定义根式

式子 $n a$ 叫做根式 (radical), 这里 $n$ 叫做根指数, $a$ 叫做被开方数.

定理

负数没有偶次方根.
为什么负数没有偶次方根?

定理

0 的任何次方根都是 0 , 记作 $n 0 = 0$ .

定理

根据 $n$ 次方根的意义, 可得

$(n a)^{n} = a .$

例如, $(5)^{2} = 5, (5 - 3)^{5} = - 3$ .

探究

$n a^{n}$ 表示 $a^{n}$ 的 $n$ 次方根, $n a^{n} = a$ 一定成立吗? 如果不一定成立, 那么 $n a^{n}$ 等于什么?

解

可以得到:
当 $n$ 为奇数时, $n a^{n} = a$ ;
当 $n$ 为偶数时, $n a^{n} = ∣ a ∣ = {a, a ⩾ 0, - a, a < 0 .$

例 1

求下列各式的值:
(1) $3 (- 8)^{3}$ ;
(2) $(- 10)^{2}$ ;
(3) $4 (3 - π)^{4}$ ;
(4) $(a - b)^{2}$ .

解:

(1) $3 (- 8)^{3} = - 8$ ;
(2) $(- 10)^{2} = ∣ - 10 ∣ = 10$ ;
(3) $4 (3 - π)^{4} = ∣ 3 - π ∣ = π - 3$ ;
(4) $(a - b)^{2} = ∣ a - b ∣ = {a - b, a ⩾ b, b - a, a < b .$

定理

根据 $n$ 次方根的定义和数的运算, 我们知道

$5 a^{10} = 5 (a^{2})^{5} = a^{2} = a^{\frac{1 0}{5}} (a > 0), 4 a^{12} = 4 (a^{3})^{4} = a^{3} = a^{\frac{1 2}{4}} (a > 0) .$

这就是说, 当根式的被开方数 (看成幂的形式) 的指数能被根指数整除时, 根式可以表示为分数指数幕的形式.

思考

当根式的被开方数的指数不能被根指数整除时, 根式是否也可以表示为分数指数幂的形式?

例子

把根式表示为分数指数幂的形式时, 例如, 把 $3 a^{2}, b, 4 c^{5}$ 等写成下列形式:

$3 a^{2} = a^{\frac{2}{3}} (a > 0), b = b^{\frac{1}{2}} (b > 0), 4 c^{5} = c^{\frac{5}{4}} (c > 0),$

我们希望整数指数幂的运算性质, 如 $(a^{k})^{n} = a^{k n}$ , 对分数指数幂仍然适用.

数学中, 引进一个新的概念或法则时, 总希望它与已有的概念或法则相容.

定义正数的正分数指数幂

由此, 我们规定, 正数的正分数指数幂的意义是

$a^{\frac{m}{n}} = n a^{m} (a > 0, m, n \in N^{*}, n > 1) .$

于是, 在条件 $a > 0, m, n \in N^{*}, n > 1$ 下, 根式都可以写成分数指数幕的形式.

定义正数的负分数指数幂

正数的负分数指数幂的意义与负整数指数幂的意义相仿, 我们规定,

$a^{- \frac{m}{n}} = \frac{1}{a ^{\frac{m}{n}}} = \frac{1}{n a ^{m}} (a > 0, m, n \in N^{*}, n > 1) .$

例子正数的负分数指数幂

例如, $5^{- \frac{4}{3}} = \frac{1}{5 ^{\frac{4}{3}}} = \frac{1}{3 5 ^{4}}, a^{- \frac{2}{3}} = \frac{1}{a ^{\frac{2}{3}}} = \frac{1}{3 a ^{2}}$ .

定义 0 的分数指数幂

与 0 的整数指数幂的意义相仿, 我们规定,

0 的正分数指数幂等于 0, 0 的负分数指数幂没有意义.

这里, 略去了规定合理性的说明.

规定了分数指数幂的意义以后, 幂 $a^{x}$ 中指数 $x$ 的取值范围就从整数拓展到了有理数.

定理有理数指数幂的运算性质

整数指数幂的运算性质对于有理数指数幂也同样适用, 即对于任意有理数 $r, s$ , 均有下面的运算性质.
(1) $a^{r} a^{s} = a^{r + s} (a > 0, r, s \in Q)$ ;
(2) $(a^{r})^{s} = a^{r s} (a > 0, r, s \in Q)$ ;
(3) $(a b)^{r} = a^{r} b^{r} (a > 0, b > 0, r \in Q)$ .

例 2

求值:
(1) $8^{\frac{2}{3}}$ ;
(2) $(\frac{1 6}{8 1})^{- \frac{3}{4}}$ .

解:

(1) $8^{\frac{2}{3}} = (2^{3})^{\frac{2}{3}} = 2^{3 \times \frac{2}{3}} = 2^{2} = 4$ ;
(2) $(\frac{1 6}{8 1})^{- \frac{3}{4}} = (\frac{8 1}{1 6})^{\frac{3}{4}} = (\frac{3 ^{4}}{2 ^{4}})^{\frac{3}{4}} = (\frac{3}{2})^{4 \times \frac{3}{4}} = (\frac{3}{2})^{3} = \frac{2 7}{8}$ .

例 3

用分数指数幂的形式表示并计算下列各式（其中 $a > 0$ ):
(1) $a^{2} \cdot 3 a^{2}$ ;
(2) $a 3 a$ .

解：

(1) $a^{2} \cdot 3 a^{2} = a^{2} a^{\frac{2}{3}} = a^{2 + \frac{2}{3}} = a^{\frac{8}{3}}$ ;
(2) $a 3 a = (a a^{\frac{1}{3}})^{\frac{1}{2}} = (a^{\frac{4}{3}})^{\frac{1}{2}} = a^{\frac{2}{3}}$ .

例 4

计算下列各式（式中字母均是正数）:
(1) $(2 a^{\frac{2}{3}} b^{\frac{1}{2}}) (- 6 a^{\frac{1}{2}} b^{\frac{1}{3}}) \div (- 3 a^{\frac{1}{6}} b^{\frac{5}{6}})$ ;
(2) $(m^{\frac{1}{4}} n^{- \frac{3}{8}})^{8}$ ;
(3) $(3 a^{2} - a^{3}) \div 4 a^{2}$ .

解:

(1)

$= = = (2 a^{\frac{2}{3}} b^{\frac{1}{2}}) (- 6 a^{\frac{1}{2}} b^{\frac{1}{3}}) \div (- 3 a^{\frac{1}{6}} b^{\frac{5}{6}}) [2 \times (- 6) \div (- 3)] a^{\frac{2}{3} + \frac{1}{2} - \frac{1}{6}} b^{\frac{1}{2} + \frac{1}{3} - \frac{5}{6}} 4 a b^{0} 4 a;$

(2)

$(m^{\frac{1}{4}} n^{- \frac{3}{8}})^{8} = (m^{\frac{1}{4}})^{8} (n^{- \frac{3}{8}})^{8} = m^{2} n^{- 3} = \frac{m ^{2}}{n ^{3}}$

(3)

$(3 a^{2} - a^{3}) \div 4 a^{2} = (a^{\frac{2}{3}} - a^{\frac{3}{2}}) \div a^{\frac{1}{2}} = a^{\frac{2}{3}} \div a^{\frac{1}{2}} - a^{\frac{3}{2}} \div a^{\frac{1}{2}} = a^{\frac{1}{6}} - a = 6 a - a .$

练习

用根式的形式表示下列各式 $(a > 0)$ :
(1) $a^{\frac{1}{2}}$ ;
(2) $a^{\frac{3}{4}}$ ;
(3) $a^{- \frac{3}{5}}$ ;
(4) $a^{- \frac{2}{3}}$ .

用分数指数幂的形式表示并计算下列各式:
(1) $3 x^{2} (x > 0)$ ;
(2) $5 (m - n)^{4} (m > n)$ ;
(3) $p^{6} p^{5} (p > 0)$ ;
(4) $\frac{a ^{3}}{a} (a > 0)$ .

计算下列各式:
(1) $(\frac{3 6}{4 9})^{\frac{3}{2}}$ ;
(2) $23 \times 3 3 1.5 \times 612$ ;
(3) $a^{\frac{1}{2}} a^{\frac{1}{4}} a^{- \frac{1}{8}} (a > 0)$ ;
(4) $2 x^{- \frac{1}{3}} (\frac{1}{2} x^{\frac{1}{3}} - 2 x^{- \frac{2}{3}})$ .

4.1.2 无理数指数幂及其运算性质

上面我们将 $a^{x} (a > 0)$ 中指数 $x$ 的取值范围从整数拓展到了有理数. 那么, 当指数 $x$ 是无理数时, $a^{x}$ 的意义是什么? 它是一个确定的数吗? 如果是, 那么它有什么运算性质?

在初中的学习中, 我们通过有理数认识了一些无理数. 类似地, 也可以通过有理数指数幂来认识无理数指数幂.

探究

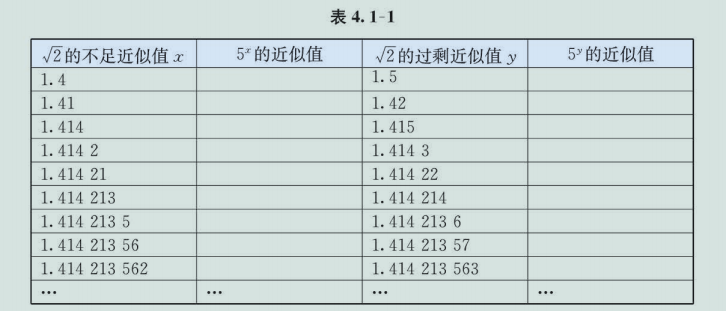
根据 $2$ 的不足近似值 $x$ 和过剩近似值 $y$ (表 4.1-1), 利用计算工具计算相应的 $5^{x}, 5^{y}$ 的近似值并填入表中, 观察它们的变化趋势, 你有什么发现?

解

可以发现, 当 $2$ 的不足近似值 $x$ 和过剩近似值 $y$ 逐渐逼近 $2$ 时, $5^{x}$ 和 $5^{y}$ 都趋向于同一个数, 这个数就是 $5^{2}$ . 也就是说, $5^{2}$ 是一串逐渐增大的有理数指数幂 $5^{1.4}, 5^{1.41}$ , $5^{1.414}, 5^{1.4142}, \dots$ 和另一串逐渐减小的有理数指数幂 $5^{1.5}, 5^{1.42}, 5^{1.415}, 5^{1.4143}, \dots$ 逐步逼近的结果, 它是一个确定的实数. 这个过程可以用图 4.1-1 表示.

思考

参照以上过程, 你能再给出一个无理数指数幂, 如 $2^{3}$ , 说明它也是一个确定的实数吗?

定义实数指数幂

一般地, 无理数指数幂 $a^{α} (a > 0, α$ 为无理数) 是一个确定的实数. 这样, 我们就将指数幂 $a^{x} (a > 0)$ 中指数 $x$ 的取值范围从整数逐步拓展到了实数. 实数指数幂是一个确定的实数.

定理实数指数幂的运算性质

整数指数幂的运算性质也适用于实数指数幂, 即对于任意实数 $r, s$ , 均有下面的运算性质.
(1) $a^{r} a^{s} = a^{r + s} (a > 0, r, s \in R)$ ;
(2) $(a^{r})^{s} = a^{r s} (a > 0, r, s \in R)$ ;
(3) $(a b)^{r} = a^{r} b^{r} (a > 0, b > 0, r \in R)$ .

练习

计算下列各式:
(1) $(2^{3} m^{3})^{23}$ ;
(2) $a^{\frac{π}{3}} a^{\frac{2 π}{3}} a^{- π}$ .

利用计算工具, 探究下列实数指数幂的变化规律:
(1) $x$ 取负实数, 使得 $∣ x ∣$ 的值逐渐增大并趋向于无穷大, 计算相应的 $2^{x} (x \in R)$ 的值, 观察变化趋势;
(2) $x$ 取正实数, 使得 $x$ 的值逐渐增大并趋向于无穷大, 计算相应的 $(\frac{1}{2})^{x} (x \in R)$ 的值, 观察变化趋势.

习题 4.1

复习巩固

求下列各式的值:
(1) $4 10 0^{4}$ ;
(2) $5 (- 0.1)^{5}$ ;
(3) $(π - 4)^{2}$ ;
(4) $6 (x - y)^{6}$ .

选择题
(1) 设 $a > 0$ , 则下列运算中正确的是（）.
(A) $a^{\frac{4}{3}} a^{\frac{3}{4}} = a$
(B) $a \div a^{\frac{2}{3}} = a^{\frac{3}{2}}$
© $a^{\frac{2}{3}} a^{- \frac{2}{3}} = 0$
(D) $(a^{\frac{1}{4}})^{4} = a$

(2) 设 $a > 0, m, n$ 是正整数，且 $n > 1$ , 则下列各式

$a^{\frac{m}{n}} = n a^{m}, a^{0} = 1, a^{- \frac{m}{n}} = \frac{1}{n a ^{m}},$

填空题
(1) 在 $(- \frac{1}{2})^{- 1}, 2^{- \frac{1}{2}}, (\frac{1}{2})^{- 1}, 2^{- 1}$ 中, 最大的数是 _ _ _
（2）按从小到大的顺序, 可将 $2^{3}, 3^{2}, π^{5}, 2^{π}$ 重新排列为 _ _ _ (可用计算工具).

用分数指数幂表示并计算下列各式 (式中字母均为正数):
(1) $\frac{b ^{3}}{a} \frac{a ^{2}}{b ^{6}}$ ;
(2) $a^{\frac{1}{2}} a^{\frac{1}{2}} a$ ;
(3) $\frac{m 3 m 4 m}{( 6 m ) ^{5} m ^{\frac{1}{4}}}$ .

计算下列各式 (式中字母均为正数):
(1) $a^{\frac{1}{3}} a^{\frac{3}{4}} a^{\frac{7}{1 2}}$ ;
(2) $a^{\frac{2}{3}} a^{\frac{3}{4}} \div a^{\frac{5}{6}}$ ;
(3) $(x^{\frac{1}{3}} y^{- \frac{3}{4}})^{12}$ ;
(4) $4 a^{\frac{2}{3}} b^{- \frac{1}{3}} \div (- \frac{2}{3} a^{- \frac{1}{3}} b^{- \frac{1}{3}})$ .

综合运用

如果在某种细菌培养过程中, 细菌每 $10 m i n$ 分裂 1 次 (1 个分裂成 2 个), 那么经过 $1 h, 1$ 个这种细菌可以分裂成 _ _ _ 个.

(1) 已知 $1 0^{m} = 2, 1 0^{n} = 3$ , 求 $1 0^{\frac{3 m - 2 n}{2}}$ 的值;
(2) 已知 $a^{2 x} = 3$ , 求 $\frac{a ^{3 x} + a ^{- 3 x}}{a ^{x} + a ^{- x}}$ 的值.

已知 $a^{\frac{1}{2}} + a^{- \frac{1}{2}} = 3$ , 求下列各式的值:
(1) $a + a^{- 1}$ ;
(2) $a^{2} + a^{- 2}$ .

拓广探索

从盛有 $1 L$ 纯酒精的容器中倒出 $\frac{1}{3} L$ , 然后用水填满; 再倒出 $\frac{1}{3} L$ , 又用水填满…
(1) 连续进行 5 次, 容器中的纯酒精还剩下多少?
(2) 连续进行 $n$ 次, 容器中的纯酒精还剩下多少?

10.

(1) 当 $n = 1, 2, 3, 10, 100, 1000, 10000, 100000, \dots$ 时, 用计算工具计算 $(1 + \frac{1}{n})^{n}$ $(n \in N^{*})$ 的值;
(2) 当 $n$ 越来越大时, $(1 + \frac{1}{n})^{n}$ 的底数越来越小, 而指数越来越大, 那么 $(1 + \frac{1}{n})^{n}$ 是否也会越来越大? 有没有最大值?