6.3 平面向量基本定理及坐标表示
2024-05-25 22:23:28 新建
上节我们学习了向量的运算, 知道位于同一直线上的向量可以由位于这条直线上的一个非零向量表示. 类似地, 平面内任一向量是否可以由同一平面内的两个不共线向量表示呢?
6.3.1 平面向量基本定理
我们知道, 已知两个力, 可以求出它们的合力; 反过来, 一个力可以分解为两个力. 如图 6.3-1, 我们可以根据解决实际问题的需要, 通过作平行四边形, 将力 分解为多组大小、方向不同的分力.
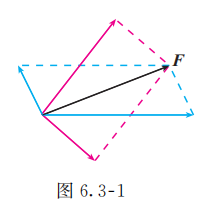
由力的分解得到启发, 我们能否通过作平行四边形, 将向量 分解为两个向量, 使向量 是这两个向量的和呢?
探究
如图 6.3-2 (1), 设 是同一平面内两个不共线的向量, 是这一平面内与 都不共线的向量. 如图 6.3-2 (2), 在平面内任取一点 , 作 . 将 按 的方向分解, 你有什么发现?

答
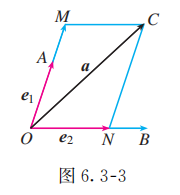
如图 6.3-3, 过点 作平行于直线 的直线, 与直线 交于点 ; 过点 作平行于直线 的直线, 与直线 交于点 , 则 . 由 与 共线, 与 共线可得, 存在实数 , 使得 , 所以 . 也就是说, 与 都不共线的向量 都可以表示成 的形式.
当 是与 或 共线的非零向量时, 也可以表示成 的形式; 当 是零向量时, 同样可以表示成 的形式. (为什么?)
// 利用信息技术工具,可以动态地展示 .
上述讨论表明, 平面内任一向量 都可以按 的方向分解, 表示成 的形式, 而且这种表示形式是唯一的. 事实上, 如果 还可以表示成 的形式,那么 . 可得 . 由此式可以推出 全为 0 (假设 不全为 0 , 不妨假设 , 则 . 由此可得 共线. 这与已知 不共线矛盾), 即 .也就是说, 有且只有一对实数 , 使 .
综上, 我们得到如下定理:
定理 平面向量基本定理
如果 是同一平面内的两个不共线向量, 那么对于这一平面内的任一向量 , 有且只有一对实数 , 使
定义 基底
若 不共线, 我们把 叫做表示这一平面内所有向量的一个基底(base).
推论
由平面向量基本定理可知, 任一向量都可以由同一个基底唯一表示, 这为我们研究问题带来了极大的方便.
例 1
如图 6.3-4, 不共线, 且 , 用 表示 .

解:
因为 ,
所以
思考
观察 , 你有什么发现?
例 2
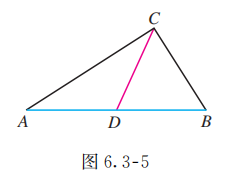
如图 6.3-5, 是 的中线, , 用向量方法证明 是直角三角形.
分析:
由平面向量基本定理可知, 任一向量都可由同一个基底表示. 本题可取 为基底, 用它表示 , . 证明 , 可得 , 从而证得 是直角三角形.
证明:
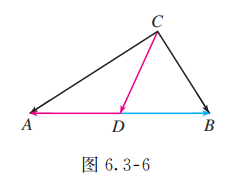
如图 6.3-6, 设 , 则 , , 于是 .
.
因为 ,
所以 .
因为 ,
所以 .
因此 .
于是 是直角三角形.
向量的数量积是否为零, 是判断相应的两条线段(或直线)是否垂直的重要方法之一。
练习
1.
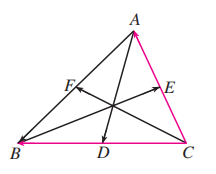
如图, 是 的三条中线, . 用 表示 .
2.
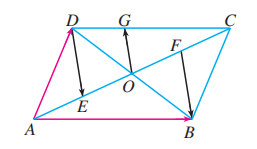
如图, 平行四边形 的两条对角线相交于点 , 点 分别是 的中点, 是 的三等分点 .
(1) 用 表示 ;
(2) 能由 (1) 得出 的关系吗?
3.
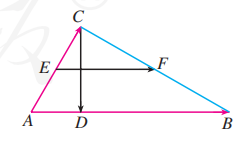
如图, 在 中, , 点 分别是 的中点. 设 .
(1) 用 表示 .
(2) 如果 有什么关系? 用向量方法证明你的结论.
6.3.2 平面向量的正交分解及坐标表示
定义 正交分解
给定平面内两个不共线的向量 ,由平面向量基本定理可知,平面上的任意向量 , 均可分解为两个向量 , 即 , 其中向量 与 共线, 向量 与 共线.
不共线的两个向量相互垂直是一种重要的情形. 把一个向量分解为两个互相垂直的向量, 叫做把向量作正交分解.
例子
如图 6.3-7, 重力 沿互相垂直的两个方向分解就是正交分解. 正交分解是向量分解中常见而实用的一种情形.
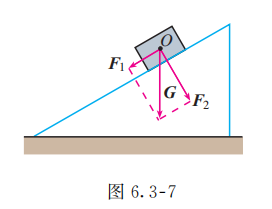
重力 可以分解为这样两个分力: 平行于斜面使木块沿斜面下滑的力 , 垂直于斜面的压力 .
在平面上, 如果选取互相垂直的向量作为基底时, 将为我们研究问题带来方便.
思考
我们知道, 在平面直角坐标系中, 每一个点都可用一对有序实数(即它的坐标)表示. 那么, 如何表示直角坐标平面内的一个向量呢?
如图 6.3-8, 在平面直角坐标系中, 设与 轴、 轴方向相同的两个单位向量分别为 , 取 作为基底. 对于平面内的任意一个向量 , 由平面向量基本定理可知, 有且只有一对实数 , 使得

定义 向量的坐标表示
这样, 平面内的任一向量 都可由 唯一确定, 我们把有序数对 叫做向量 的坐标, 记作
其中, 叫做 在 轴上的坐标, 叫做 在 轴上的坐标, (1) 叫做向量 的坐标表示.
显然, .
定理 向量的坐标与点的坐标之间的联系
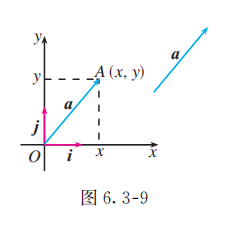
如图 6.3-9, 在直角坐标平面中, 以原点 为起点作 , 则点 的位置由向量 唯一确定.
设 , 则向量 的坐标 就是终点 的坐标; 反过来, 终点 的坐标 也就是向量 的坐标. 因为 , 所以终点 的坐标 就是向量 的坐标. 这样就建立了向量的坐标与点的坐标之间的联系.
例 3
如图 6.3-10, 分别用基底 表示向量 , 并求出它们的坐标.

解:
由图 6.3-10 可知, ,所以 .
同理,
6.3.3 平面向量加、减运算的坐标表示
思考
已知 , 你能得出 的坐标吗?
答
即
同理可得
定理
这就是说, 两个向量和 (差) 的坐标分别等于这两个向量相应坐标的和 (差).
例 4
已知 , 求 的坐标.
解:
探究
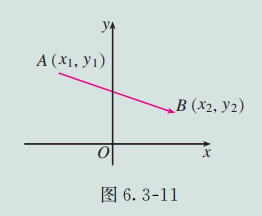
如图 6.3-11, 已知 ,你能得出 的坐标吗?
答
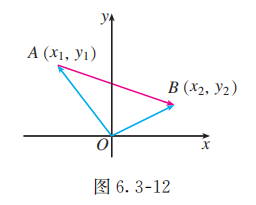
如图 6.3-12, 作向量 , 则
定理
因此, 一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标.
例 5
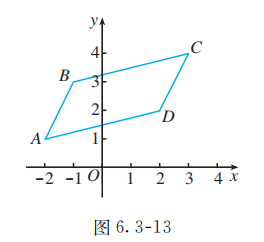
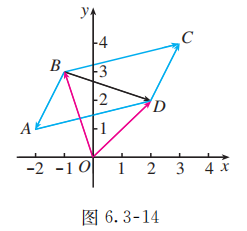
如图 6.3-13, 已知平行四边形 的三个顶点 的坐标分别是 , 求顶点 的坐标.
解
解法 1: 如图 6.3-13, 设顶点 的坐标为 .
因为
又 ,
所以 .
即 解得
所以顶点 的坐标为 .
解法 2: 如图 6.3-14, 由向量加法的平行四边形法则可知
而
所以顶点 的坐标为 .
思考
你能比较一下两种解法在思想方法上的异同点吗?
练习
1.
在下列各小题中, 已知向量 的坐标, 分别求 的坐标:
(1) ;
(2) ;
(3) ;
(4) .
2.
在下列各小题中, 已知 两点的坐标, 分别求 的坐标:
(1) ;
(2) ;
(3) ;
(4) .
3.
若点 , 则 与 有什么位置关系? 证明你的猜想.
6.3.4 平面向量数乘运算的坐标表示
思考
已知 , 你能得出 的坐标吗?
答
即
定理
这就是说, 实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
例 6
已知 , 求 的坐标.
解:
.
探究
如何用坐标表示两个向量共线的条件?
定理
设 , 其中 . 我们知道, 共线的充要条件是存在实数 , 使
如果用坐标表示, 可写为
即
消去 , 得
定理
这就是说, 向量 共线的充要条件是
例 7
已知 , 且 , 求 .
解:
因为 ,
所以 .
解得 .
例 8
已知 , 判断 , 三点之间的位置关系.
解:
在平面直角坐标系中作出 三点(图 6.3-15).观察图形, 我们猜想 三点共线. 下面来证明.
因为 , ,
又 ,
所以 .
又 直线 , 直线 有公共点 ,
所以 三点共线.
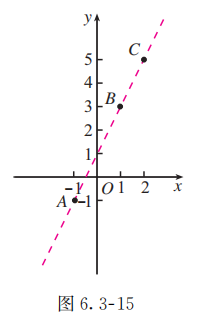
例 9
设 是线段 上的一点, 点 的坐标分别是 .
(1) 当 是线段 的中点时, 求点 的坐标;
(2) 当 是线段 的一个三等分点时,求点 的坐标.
解:
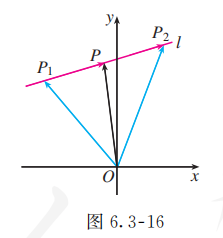
(1) 如图 6.3-16, 由向量的线性运算可知
所以, 点 的坐标是 .
(2) 如图 6.3-17, 当点 是线段 的一个三等分点时, 有两种情况, 即 或 .

如果 (图 6.3-17(1)), 那么
即点 的坐标是 .
同理, 如果 (图 6.3-17(2)), 那么点 的坐标是 .
定理
若点 的坐标分别为 , , 线段 的中点 的坐标为 , 则
此公式为线段 的中点坐标公式.
探究
如图 6.3-18, 线段 的端点 的坐标分别是 ,点 是直线 上的一点. 当 时, 点 的坐标是什么?

练习
1.
已知 , 求 的坐标.
2.
当 为何值时, 与 共线?
3.
若点 , 则 与 是否共线?
4.
求线段 的中点坐标:
(1) ;
(2) ;
(3) .
5.
已知点 , 向量 , 点 是线段 的三等分点, 求点 的坐标.
6.3.5 平面向量数量积的坐标表示
探究
已知 , 怎样用 与 的坐标表示 呢?
答
因为 ,
所以 .
又 ,
所以 .
定理
这就是说, 两个向量的数量积等于它们对应坐标的乘积的和.
定理
由此可得
(1) 若 , 则 , 或 .
如果表示向量 的有向线段的起点和终点的坐标分别为 , 那么
(2) 设 , 则
例 10
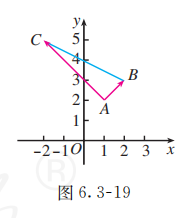
若点 , 则 是什么形状? 证明你的猜想.
解:
如图 6.3-19, 在平面直角坐标系中画出点 , 我们发现 是直角三角形. 证明如下.
因为 , ,
所以 .
于是 .
因此, 是直角三角形.
定理
设 都是非零向量, 是 与 的夹角, 根据向量数量积的定义及坐标表示可得
例 11
设 , 求 及 的夹角 (精确到 ).
解:
因为 , 所以用计算器计算可得
利用计算工具可得 .
例 12
用向量方法证明两角差的余弦公式
证明:
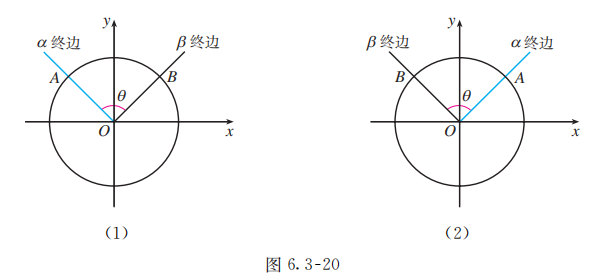
如图 6.3-20, 在平面直角坐标系 内作单位圆 , 以 轴的非负半轴为始边作角 , 它们的终边与单位圆 的交点分别为 . 则
由向量数量积的坐标表示, 有
设 与 的夹角为 , 则
所以
另一方面, 由图 6.3-20 (1) 可知, ; 由图 6.3-20 (2) 可知, . 于是 . 所以
于是
运用向量工具进行探索, 过程多么简洁啊!
练习
1.
已知 , 求 .
2.
已知 . 求 , .
3.
已知 , 利用计算工具, 求 与 的夹角 (精确到 ).
习题 6.3
复习巩固
1.
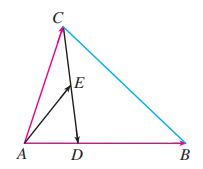
如图, 在 中, , 点 是 的中点. 设 , 用 表示 .
2.
已知作用在坐标原点的三个力分别为 , , 求作用在原点的合力 的坐标.
3.
在下列各小题中, 已知向量 的坐标, 以及表示 的有向线段 的起点 的坐标, 求终点 的坐标:
(1) ;
(2) ;
(3) .
4.
已知平行四边形 的顶点 , 求顶点 的坐标.
5.
已知点 , 且 , 求点 及向量 的坐标.
6.
已知点 , 且 , 求点 的坐标.
7.
你认为下列各组点具有什么样的位置关系? 证明你的猜想.
(1) ;
(2) ;
(3) .
8.
分别在平面直角坐标系中作出下列各组点, 猜想以 为顶点的三角形的形状, 然后给出证明:
(1) ;
(2) ;
(3) .
9.
已知 , 且 , 求 的坐标.
10.
已知 , 求与 垂直的单位向量的坐标.
综合运用
11.
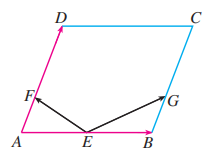
如图, 在平行四边形 中, 点 是 的中点, 点 分别是 的三等分点 . 设 ,
(1) 用 表示 .
(2) 如果 有什么位置关系? 用向量方法证明你的结论.
12.
已知点 . 当 时, 分别求点 的坐标.
13.
已知 , 点 在线段 的延长线上, 且 , 求点 的坐标.
14.
求证: 以 为顶点的四边形是一个矩形.
拓广探索
15.
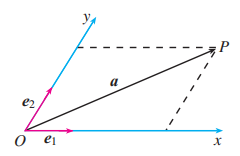
如图, 设 是平面内相交成 角的两条数轴, , 分别是与 轴、 轴正方向同向的单位向量. 若向量 , 则把有序数对 叫做向量 在坐标系 中的坐标. 设 ,
(1) 计算 的大小;
(2) 根据平面向量基本定理判断, 本题中对向量坐标的规定是否合理.
16.
用向量方法证明: 对于任意的 , 恒有不等式