6.5 小结
2024-06-08 22:16:49 新建
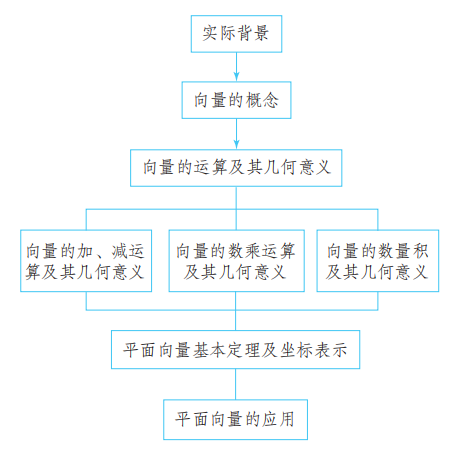
本章知识结构
回顾与思考
向量是刻画现实世界中 “既有大小又有方向的量”的数学工具. 本章我们类比数及其运算, 学习了向量及其运算, 以及向量运算的几何意义, 并用向量方法解决了一些几何问题、物理问题, 特别是用向量方法研究了任意三角形的边角关系, 得到了正弦定理、余弦定理. 其研究的内容、过程是:向量现实背景、几何背景 — 向量的概念 — 向量的运算和运算律 — 相关知识的联系 — 实际应用.
我们通过分析位移、力、速度等了解了向量的实际背景, 引入了向量概念. 其中, 位移是向量的最佳现实模型. 定义向量概念时, 我们首先明确了向量的内涵(大小、方向), 并用有向线段表示向量, 然后认识了单位向量、零向量等 “特殊” 向量, 明确了两个向量的平行、相等、共线等 “特殊关系”. 这里, 明确数学对象的内涵及表示是定义一个数学对象的基本要求.
向量的运算, 是 “带方向的量的运算”. 这里, 如何对方向进行运算是核心问题.“位移的合成” 很好地解释了 “两个方向之和”, 以此为背景我们定义了向量加法的三角形法则; 而以 “力的合成”为背景定义了向量加法的平行四边形法则. “定义了一种运算就要研究运算律”, 向量加法满足交换律、结合律, 而交换律就是 “平行四边形的两组对边分别平行且相等”的向量表达式.
类比数 的整数倍 是 个 相加的总和, 可以把 个向量 相加的总和写为 . 一般地, 实数 与向量 的乘积 是一个向量, 它所满足的运算律 (1) , (2) , (3) 与实数乘法的运算律有所差异. 这里有两个特别有用的结论: 一是 是 “相似三角形对应边的比等于相似比”的代数化形式; 二是 与 共线, 由此,两个非零向量 共线(平行)的充要条件是 . 其实, 联系数轴概念,如果设 是与数轴 的方向相同的单位向量, 数轴上任意一点 的坐标为 , 那么 ; 反之也对.
以物理中力做功为背景, 我们定义了两个向量的数量积, 并研究了它的运算律, 其中分配律是非常重要的. 向量数量积不同于向量的线性运算, 因为它的运算结果是数量, 不是向量. 向量数量积与距离、夹角等紧密相联, 用它可以解决一些涉及距离、夹角的几何问题.
为了彻底实现几何的代数化, 需要进一步研究平面上点的向量表示问题. 对于平面 上任意一点 , 可以利用向量的加法和数乘向量, 把平面 上的向量 表示为 (其中向量 不共线), 从而使它成为可运算的对象. 在解决几何问题时, 这种表示发挥了基础性作用, 因此我们把它叫做平面向量基本定理. 特别地, 我们以 为基底, 建立了平面直角坐标系 中的向量 与点 的坐标间的一一对应.
通过本章的学习我们发现, 与集合是一种特殊的运算对象类似, 向量也是一种不同于实数的运算对象, 而向量运算与实数运算既有差别又有共性. 在定义向量的运算法则, 探索其相应的运算律时, 我们总是类比数及其运算来发现和提出问题. 因此, 本章的学习对于提高我们对数学运算的认识水平, 理解数学运算和逻辑推理的关系等,都有很大的帮助.
用向量方法解决平面几何问题, 其特色是仅用向量加法法则(称为 “向量回路” )、向量数乘的意义及其运算律、向量数量积的意义和运算律(特别是相互垂直的向量数量积为 0 ), 以及平面向量基本定理等 4 条基本法则、定理. 与平面几何有大量基本事实、定理比较, 向量法在解决某些几何问题时简捷得多. 例如, 利用 “三角形回路” 和数量积, 我们非常快捷地得到了余弦定理.
平面向量及其运算与空间向量及其运算紧密联系, 与数及其运算也直接相关, 在其他学科 (特别是物理) 中也有广泛应用. 这种联系我们可以用下面的框图表示.
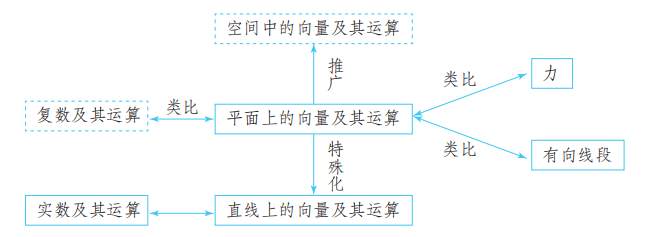
请你带着下面的问题, 复习一下全章的内容吧!
- 向量的概念是什么? 用有向线段如何表示一个向量?
- 你能说说向量的加法、减法、向量的数乘运算、向量的数量积是如何定义的吗?
- 运算律是运算的灵魂. 你能通过实例, 说明向量的加法、向量的数乘运算、向量的数量积有哪些运算律吗? 这些运算律的几何意义是什么? 这些运算律与数的运算律的联系与区别是什么?
- 平面向量基本定理是什么? 这个定理的意义是什么? 你能说说什么是向量的坐标表示吗?
- 你能用向量的坐标表示描述向量共线的条件吗? 你能用向量的坐标表示描述向量的长度及两个向量的夹角吗?
- 用向量方法解决平面几何问题要经过哪些步骤? 要注意哪些问题? 你能通过实例说明如何选择基底吗?
- 你能通过实例, 说明向量在物理中的应用吗?
- 回顾用向量方法推导正弦定理、余弦定理的过程, 你能总结一下其中的思想方法吗?
复习参考题 6
复习巩固
1.
判断下列命题是否正确 (正确的在括号内打 “√”,错误的打 “×”).
(1) .
(2) .
(3) .
(4) .
2.
选择题
(1) 如果 是两个单位向量, 那么下列四个结论中正确的是().
(A)
(B)
(C)
(D)
(2) 对于任意两个向量 和 , 下列命题中正确的是().
(A) 若 满足 , 且 与 同向, 则
(B)
(C)
(D)
(3) 在四边形 中, 若 , 则().
(A) 四边形 是矩形
(B) 四边形 是菱形
(C) 四边形 是正方形
(D) 四边形 是平行四边形
(4) 设 是非零向量, 是非零实数,下列结论中正确的是().
(A) 与 的方向相反
(B)
(C) 与 的方向相同
(D)
(5) 设 是平行四边形 的对角线的交点, 为任意一点,则 ( ).
(A)
(B)
(C)
(D)
(6) 在下列各组向量中, 可以作为基底的是().
(A)
(B)
(C)
(D)
3.
已知六边形 为正六边形, 且 , 分别用 表示 ,
4.
已知平面直角坐标系中, 点 为原点, .
(1) 求 的坐标及 的值;
(2) 若 , 求 与 的坐标;
(3) 求 的值.
5.
已知点 . 若 , 则点 的坐标是什么?
6.
已知向量 , 求满足 的 和 的值.
7.
已知 的顶点坐标分别为 , 求 的值.
8.
已知向量 . 当 为何值时, 与 垂直?
9.
已知向量 与 的夹角为 , 求 的值.
10.
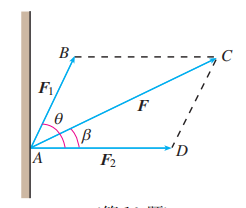
如图, 支座 受 两个力的作用, 已知 与水平线成 角, 沿水平方向, 与 的合力 的大小为 , 求 以及 与 的夹角 的余弦值.
11.
在 中, 分别根据下列条件解三角形(角度精确到 , 边长精确到 ):
(1) ;
(2) ;
(3) ;
(4) .
12.
海中有一座小岛, 周围 mile 内有暗礁. 一艘海轮由西向东航行, 望见该岛在北偏东 ;海轮航行 mile 以后, 望见该岛在北偏东 . 如果这艘海轮不改变航向继续前进, 有没有触礁的危险?
综合运用
13.
选择题
(1) 已知 是不共线的向量,且 , 则().
(A) 三点共线
(B) 三点共线
(C) 三点共线
(D) 三点共线
(2) 已知正方形 的边长为 , 则 ( ).
(A) 0
(B) 3
(C)
(D)
(3) 已知 , 且四边形 为平行四边形, 则 ( ).
(A)
(B)
(C)
(D)
(4) 若 是夹角为 的两个单位向量, 则 与 的夹角为 ( ).
(A)
(B)
(C)
(D)
(5) 已知等边三角形 的边长为 , 那么 ( ).
(A)
(B)
(C)
(D)
(6) 若平面向量 两两的夹角相等, 且 , 则 ( ).
(A) 2
(B) 5
(C) 2 或 5
(D) 或
14.
已知 为非零向量, 证明下列结论, 并解释其几何意义.
(1) ;
(2) 若 , 则 .
15.
已知 , 向量 满足条件 , . 求证: 是等边三角形.
16.
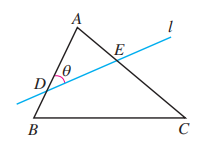
如图, 已知 , 任意点 关于点 的对称点为 , 点 关于点 的对称点为 , 用 表示向量 . (本题可以运用信息技术发现规律)
17.
一个人骑自行车由 地出发向东骑行了 到达 地, 然后由 地向南偏东 方向骑行了 到达 地, 再从 地向北偏东 骑行了 到达 地, 求这个人由 地到 地的位移 (角度精确到 )。
拓广探索
18.
设计一种借助两个观察点 (其中 之间的距离是 )测量航船的航向与速度的方法.
19.
如图, 直线 与 的边 分别相交于点 . 设 , 请用向量方法探究 与 的边和角之间的等量关系.