4.3 对数

2024-02-14 21:30:16 新建

在 4.2.1 的问题 1 中, 通过指数幂运算, 我们能从 $y = 1.1 1^{x}$ 中求出经过 $x$ 年后 $B$ 地景区的游客人次为 2001 年的倍数 $y$ . 反之, 如果要求经过多少年游客人次是 2001 年的 2 倍, 3 倍, 4 倍, $\dots$ , 那么该如何解决?

4.3.1 对数的概念

上述问题实际上就是从 $2 = 1.1 1^{x}, 3 = 1.1 1^{x}, 4 = 1.1 1^{x}, \dots$ 中分别求出 $x$ , 即已知底数和幂的值, 求指数. 这是本节要学习的对数.

定义对数

一般地, 如果 $a^{x} = N (a > 0$ , 且 $a \neq = 1)$ , 那么数 $x$ 叫做以 $a$ 为底 $N$ 的对数 (logarithm), 记作

$x = lo g_{a} N,$

其中 $a$ 叫做对数的底数, $N$ 叫做真数.

“log” 是 logarithm （对数）的缩写.

例如,

由于 $2 = 1.1 1^{x}$ , 所以 $x$ 就是以 1.11 为底 2 的对数, 记作 $x = lo g_{1.11} 2$ ; 再如, 由于 $4^{2} = 16$ , 所以以 4 为底 16 的对数是 2 , 记作 $lo g_{4} 16 = 2$ .

定义常用对数，自然对数

通常, 我们将以 10 为底的对数叫做常用对数 (common logarithm), 并把 $lo g_{10} N$ 记为 $l g N$ . 另外, 在科技、经济以及社会生活中经常使用以无理数 $e = 2.71828 \dots$ 为底数的对数, 以 $e$ 为底的对数称为自然对数 (natural logarithm), 并把 $lo g_{e} N$ 记为 $ln N$ .

实践

通过查询互联网，进一步了解无理数 $e$ 、常用对数和自然对数.

定理对数与指数间的关系

根据对数的定义, 可以得到对数与指数间的关系:

当 $a > 0, a \neq = 1$ 时, $a^{x} = N \Leftrightarrow x = lo g_{a} N$ .

定理对数的性质

由指数与对数的这个关系, 可以得到关于对数的如下结论:

负数和 0 没有对数;
$lo g_{a} 1 = 0, lo g_{a} a = 1$ .

请你利用对数与指数间的关系证明这两个结论.

例 1

把下列指数式化为对数式, 对数式化为指数式:
(1) $5^{4} = 625$ ;
(2) $2^{- 6} = \frac{1}{6 4}$ ;
(3) $(\frac{1}{3})^{m} = 5.73$ ;
(4) $lo g_{\frac{1}{2}} 16 = - 4$ ;
(5) $l g 0.01 = - 2$ ;
(6) $ln 10 = 2.303$ .

解:

(1) $lo g_{5} 625 = 4$ ;
(2) $lo g_{2} \frac{1}{6 4} = - 6$ ;
(3) $lo g_{\frac{1}{3}} 5.73 = m$ ;
(4) $(\frac{1}{2})^{- 4} = 16$ ;
(5) $1 0^{- 2} = 0.01$ ;
(6) $e^{2.303} = 10$ .

例 2

求下列各式中 $x$ 的值:
(1) $lo g_{64} x = - \frac{2}{3}$ ;
(2) $lo g_{x} 8 = 6$ ;
(3) $l g 100 = x$ ;
(4) $- ln e^{2} = x$ .

解:

(1) 因为 $lo g_{64} x = - \frac{2}{3}$ , 所以

$x = 6 4^{- \frac{2}{3}} = (4^{3})^{- \frac{2}{3}} = 4^{- 2} = \frac{1}{1 6} .$

(2) 因为 $lo g_{x} 8 = 6$ , 所以 $x^{6} = 8$ . 又 $x > 0$ , 所以

$x = 8^{\frac{1}{6}} = (2^{3})^{\frac{1}{6}} = 2^{\frac{1}{2}} = 2 .$

(3) 因为 $l g 100 = x$ , 所以

$1 0^{x} = 100, 1 0^{x} = 1 0^{2},$

于是

$x = 2 .$

(4) 因为 $- ln e^{2} = x$ ，所以

$ln e^{2} = - x, e^{2} = e^{- x},$

于是

$x = - 2 .$

练习

把下列指数式写成对数式, 对数式写成指数式:
(1) $2^{3} = 8$ ;
(2) $e^{3} = m$ ;
(3) $2 7^{- \frac{1}{3}} = \frac{1}{3}$ ;
(4) $lo g_{3} 9 = 2$ ;
(5) $l g n = 2.3$ ;
(6) $lo g_{3} \frac{1}{8 1} = - 4$ .

求下列各式的值:
(1) $lo g_{5} 25$ ;
(2) $lo g_{0.4} 1$ ;
(3) $ln \frac{1}{e}$ ;
(4) $l g 0.001$ .

求下列各式中 $x$ 的值:
(1) $lo g_{\frac{1}{3}} x = - 3$ ;
(2) $lo g_{x} 49 = 4$ ;
(3) $l g 0.00001 = x$ ;
(4) $ln e = - x$ .

4.3.2 对数的运算

在引入对数之后, 自然应研究对数的运算性质. 你认为可以怎样研究?

探究

我们知道了对数与指数间的关系, 能否利用指数幂运算性质得出相应的对数运算性质呢?

解

设

$M = a^{m}, N = a^{n},$

因为

$a^{m} a^{n} = a^{m + n},$

所以

$M N = a^{m + n} .$

根据对数与指数间的关系可得

$lo g_{a} M = m, lo g_{a} N = n, lo g_{a} (M N) = m + n .$

这样, 就得到了对数的一个运算性质:

$lo g_{a} (M N) = lo g_{a} M + lo g_{a} N .$

同样地, 同学们可以仿照上述过程, 由 $a^{m} \div a^{n} = a^{m - n}$ 和 $(a^{m})^{n} = a^{m n}$ , 自己推出对数运算的其他性质.

于是, 我们得到如下的对数运算性质.

定理对数运算性质

如果 $a > 0$ , 且 $a \neq = 1, M > 0, N > 0$ , 那么
(1) $lo g_{a} (M N) = lo g_{a} M + lo g_{a} N$ ；
(2) $lo g_{a} \frac{M}{N} = lo g_{a} M - lo g_{a} N$ ；
(3) $lo g_{a} M^{n} = n lo g_{a} M (n \in R)$ .

例 3

求下列各式的值:
(1) $l g 5100$ ;
(2) $lo g_{2} (4^{7} \times 2^{5})$ .

解:

(1)

$l g 5100 = l g 10 0^{\frac{1}{5}} = \frac{1}{5} l g 100 = \frac{2}{5};$

(2)

$lo g_{2} (4^{7} \times 2^{5}) = lo g_{2} 4^{7} + lo g_{2} 2^{5} = 7 lo g_{2} 4 + 5 lo g_{2} 2 = 7 \times 2 + 5 \times 1 = 19$

例 4

用 $ln x, ln y, ln z$ 表示 $ln \frac{x ^{2} y}{3 z}$ .

解:

$ln \frac{x ^{2} y}{3 z} = ln (x^{2} y) - ln 3 z = ln x^{2} + ln y - ln 3 z = 2 ln x + \frac{1}{2} ln y - \frac{1}{3} ln z .$

数学史上, 人们经过大量的努力, 制作了常用对数表和自然对数表, 只要通过查表就能求出任意正数的常用对数或自然对数. 现在, 利用计算工具, 也可以直接求出任意正数的常用对数或自然对数. 这样, 如果能将其他底的对数转换为以 10 或 $e$ 为底的对数, 就能方便地求出这些对数.

探究

(1) 利用计算工具求 $ln 2, ln 3$ 的近似值;
(2) 根据对数的定义, 你能利用 $ln 2, ln 3$ 的值求 $lo g_{2} 3$ 的值吗?
(3) 根据对数的定义，你能用 $lo g_{c} a, lo g_{c} b$ 表示 $lo g_{a} b (a > 0$ , 且 $a \neq = 1; b > 0$ ; $c > 0$ , 且 $c \neq = 1$ ) 吗?

定理对数换底公式

$lo g_{a} b = \frac{lo g _{c} b}{lo g _{c} a} (a > 0, 且 a \neq = 1; b > 0; c > 0, 且 c \neq = 1) .$

证明

设 $lo g_{a} b = x$ , 则 $a^{x} = b$ , 于是

$lo g_{c} a^{x} = lo g_{c} b .$

根据性质（3）得 $x lo g_{c} a = lo g_{c} b$ , 即

$lo g_{a} b = \frac{lo g _{c} b}{lo g _{c} a} (a > 0, 且 a \neq = 1; b > 0; c > 0, 且 c \neq = 1) .$

例子

在 4.2.1 的问题 1 中, 求经过多少年 B 地景区的游客人次是 2001 年的 2 倍, 就是计算 $x = lo g_{1.11} 2$ 的值. 由换底公式, 可得

$x = lo g_{1.11} 2 = \frac{l g 2}{l g 1 . 1 1} .$

利用计算工具, 可得

$x = \frac{l g 2}{l g 1 . 1 1} \approx 6.64 \approx 7 .$

由此可得, 大约经过 7 年, B 地景区的游客人次就达到 2001 年的 2 倍.
类似地, 可以求出游客人次是 2001 年的 3 倍, 4 倍, $\dots$ 所需要的年数.

例 5

尽管目前人类还无法准确预报地震, 但科学家通过研究, 已经对地震有所了解, 例如, 地震时释放出的能量 $E$ (单位: 焦耳)与地震里氏震级 $M$ 之间的关系为

$l g E = 4.8 + 1.5 M .$

2011 年 3 月 11 日, 日本东北部海域发生里氏 9.0 级地震, 它所释放出来的能量是 2008 年 5 月 12 日我国汶川发生里氏 8.0 级地震的多少倍（精确到 1)?

解:

设里氏 9.0 级和 8.0 级地震的能量分别为 $E_{1}$ 和 $E_{2}$ .
由 $l g E = 4.8 + 1.5 M$ , 可得

$l g E_{1} = 4.8 + 1.5 \times 9.0, l g E_{2} = 4.8 + 1.5 \times 8.0 .$

于是,

$l g \frac{E _{1}}{E _{2}} = l g E_{1} - l g E_{2} = (4.8 + 1.5 \times 9.0) - (4.8 + 1.5 \times 8.0) = 1.5 .$

利用计算工具可得, $\frac{E _{1}}{E _{2}} = 1 0^{1.5} \approx 32$ .
虽然里氏 9.0 级地震与里氏 8.0 级地震仅相差 1 级, 但前者释放出来的能量却是后者的约 32 倍.

思考

想一想，为什么两次地震的里氏震级仅差1级，而释放的能量却相差那么多呢?

练习

求下列各式的值:
(1) $lo g_{3} (27 \times 9^{2})$ ;
(2) $l g 5 + l g 2$ ;
(3) $ln 3 + ln \frac{1}{3}$ ;
(4) $lo g_{3} 5 - lo g_{3} 15$ .

用 $l g x, l g y, l g z$ 表示下列各式:
(1) $l g (x y z)$ ;
(2) $l g \frac{x y ^{2}}{z}$ ;
(3) $l g \frac{x y ^{3}}{z}$ ;
(4) $l g \frac{x}{y ^{2} z}$ .

化简下列各式:
(1) $lo g_{2} 3 \times lo g_{3} 4 \times lo g_{4} 5 \times lo g_{5} 2$ ;
(2) $2 (lo g_{4} 3 + lo g_{8} 3) (lo g_{3} 2 + lo g_{9} 2)$ .

习题 4.3

复习巩固

把下列指数式写成对数式, 对数式写成指数式:
(1) $3^{x} = 1$ ;
(2) $4^{x} = \frac{1}{6}$ ;
(3) $1 0^{x} = 6$ ;
(4) $e^{x} = 25$ ;
(5) $x = lo g_{5} 27$ ;
(6) $x = lo g_{7} \frac{1}{3}$ ;
(7) $x = l g 0.3$ ;
(8) $x = ln 3$ .

选择题
(1) 使式子 $lo g_{(2 x - 1)} (2 - x)$ 有意义的 $x$ 的取值范围是 ( ).
(A) $x > 2$
(B) $x < 2$
© $\frac{1}{2} < x < 2$
(D) $\frac{1}{2} < x < 2$ , 且 $x \neq = 1$
(2) 若 $l g a (a > 0)$ 与 $l g b (b > 0)$ 互为相反数, 则 ( ).
(A) $a + b = 0$
(B) $a - b = 0$
© $a b = 1$
(D) $\frac{a}{b} = 1$

求下列各式的值:
(1) $lo g_{a} 2 + lo g_{a} \frac{1}{2}$ ;
(2) $lo g_{3} 18 - lo g_{3} 2$ ;
(3) $l g \frac{1}{4} - l g 25$ ;
(4) $2 lo g_{5} 25 - 3 lo g_{2} 64$ ;
(5) $lo g_{2} (lo g_{2} 16)$ ;
(6) $lo g_{2} 25 \times lo g_{3} 4 \times lo g_{5} 9$ .

求满足下列条件的 $x$ 的值:
(1) $ln x = ln a + ln b$ ;
(2) $l g x = 3 l g n - l g m$ ;
(3) $lo g_{a} x = \frac{1}{2} lo g_{a} b - lo g_{a} c$ ;
(4) $lo g_{2} [lo g_{3} (lo g_{4} x)] = 0$ .

综合运用

已知 $l g 2 = a, l g 3 = b$ , 求下列各式的值:
(1) $l g 6$ ;
(2) $lo g_{3} 4$ ;
(3) $lo g_{2} 12$ ;
(4) $l g \frac{3}{2}$ .

求满足下列条件的各式的值:
(1) 若 $x lo g_{3} 4 = 1$ , 求 $4^{x} + 4^{- x}$ 的值;
(2) 若 $f (x) = 3^{x}$ , 求 $f (lo g_{3} 2)$ 的值.

证明:
(1) $lo g_{a} b \cdot lo g_{b} c \cdot lo g_{c} a = 1$ ；
(2) $lo g_{a^{m}} b^{n} = \frac{n}{m} lo g_{a} b$ .

某地 GDP 的年平均增长率为 $6.5 %$ , 按此增长率, 多少年后该地 GDP 会翻两番?

拓广探索

我们可以把 $(1 + 1 %)^{365}$ 看作每天的 “进步” 率都是 $1 %$ , 一年后是 $1.0 1^{365}$ ; 而把 $(1 - 1 %)^{365}$ 看作每天的 “落后” 率都是 $1 %$ , 一年后是 $0.9 9^{365}$ . 利用计算工具计算并回答下列问题:
(1) 一年后 “进步” 的是 “落后” 的多少倍?
(2) 大约经过多少天后 “进步” 的分别是 “落后” 的 10 倍、100 倍、1000 倍?

10.

酒驾是严重危害交通安全的违法行为. 为了保障交通安全, 根据国家有关规定: $100 m L$ 血液中酒精含量达到 $20 \sim 79 m g$ 的驾驶员即为酒后驾车, $80 m g$ 及以上认定为醉酒驾车. 假设某驾驶员喝了一定量的酒后, 其血液中的酒精含量上升到了 $1 m g / m L$ . 如果在停止喝酒以后,他血液中酒精含量会以每小时 $30 %$ 的速度减少, 那么他至少经过几个小时才能驾驶?

阅读与思考

对数的发明

16、17 世纪之交, 天文、航海、工程、贸易以及军事快速发展, 对大数的运算提出了更高的要求, 改进数字计算方法、提高计算速度和准确度成了当务之急.苏格兰数学家纳皮尔 (J. Napier, 1550-1617) 在研究天文学的过程中, 经过对运算体系的多年研究, 最终找到了简化大数运算的有效工具, 于 1614 年出版了《奇妙的对数定律说明书》, 标志着对数的诞生. 在这本书中, 纳皮尔借助运动学,用几何术语阐述了对数方法.

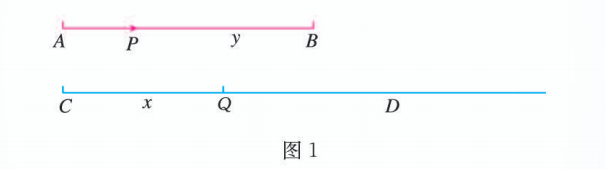
如图 1, 假定两点 $P, Q$ 以相同的初速度运动. 点 $Q$ 沿直线 $C D$ 作匀速运动, $C Q = x$ ; 点 $P$ 沿线段 $A B$ (长度为 $1 0^{7}$ 单位) 运动, 它在任何一点的速度值等于它尚未经过的距离 $(P B = y)$ . 令 $P$ 与 $Q$ 同时分别从 $A, C$ 出发, 那么, 定义 $x$ 为 $y$ 的对数.

用现在的数学符号来叙述, 纳皮尔的对数中, $x$ 与 $y$ 的对应关系就是

$y = 1 0^{7} (\frac{1}{e})^{\frac{x}{1 0 ^{7}}} .$

其中, $e$ 为自然对数的底. 利用对数, 纳皮尔制作了 $0^{\circ} \sim 9 0^{\circ}$ 每隔 $1^{'}$ 的八位三角函数表, 但是这种方法不够方便和简捷.

把对数加以改造并使之广泛流传的是纳皮尔的朋友布里格斯 (H. Briggs, 1561-1631). 他通过研究《奇妙的对数定律说明书》, 感到其中的对数用起来很不方便, 于是与纳皮尔商定, 使 1 的对数为 0,10 的对数为 1 , 这样就得到了现在所用的以 10 为底的常用对数. 由于我们的数系是十进制, 因此它在数值计算上具有优越性. 1624 年, 布里格斯出版了《对数算术》, 公布了以 10 为底包含 $1 \sim 20000$ 及 $90000 \sim 100000$ 的 14 位常用对数表.

根据对数运算原理，人们还发明了对数计算尺. 300 多年来，对数计算尺一直是科学工作者, 特别是工程技术人员必备的计算工具, 直到 20 世纪 70 年代才让位给电子计算器. 尽管作为一种计算工具, 对数计算尺、对数表现在都不再重要了, 但是, 对数的思想方法, 即把乘方和乘法运算分别转化为乘法和加法, 在今天仍然具有生命力.

从对数发明的过程可以发现, 纳皮尔在讨论对数概念时, 并没有使用指数与对数的互逆关系, 主要是当时还没有明确的指数概念, 就连指数符号也是在 20 多年后的 1637 年由法国数学家笛卡儿开始使用. 直到 18 世纪, 瑞士数学家欧拉才发现指数与对数的互逆关系, 并在 1770 年出版的一部著作中, 首先使用 $y = a^{x}$ 来定义 $x = lo g_{a} y$ . 他指出, “对数源出于指数”. 然而对数的发明先于指数, 这成为数学史上的珍闻.

从对数的发明过程可以看到, 社会生产、科学技术的需要是数学发展的主要动力. 建立对数与指数之间联系的过程表明, 使用较好的符号体系和运算规则不仅对数学的发展至关重要, 而且可以大大减轻人们的思维负担.