3.1 函数的概念及其表示
2024-01-25 22:19:18 新建
在初中我们已经接触过函数的概念, 知道函数是刻画变量之间对应关系的数学模型和工具. 例如, 正方形的周长 与边长 的对应关系是 , 而且对于每一个确定的 都有唯一的 与之对应, 所以 是 的函数. 这个函数与正比例函数 相同吗? 又如, 你能用已有的函数知识判断 与 是否相同吗? 要解决这些问题, 就需要进一步学习函数概念.
3.1.1 函数的概念
先分析以下问题.
问题 1
某 “复兴号” 高速列车加速到 后保持匀速运行半小时. 这段时间内, 列车行进的路程 (单位: ) 与运行时间 (单位: h) 的关系可以表示为
这里, 和 是两个变量, 而且对于 的每一个确定的值, 都有唯一确定的值与之对应, 所以 是 的函数.
思考
有人说: “根据对应关系 , 这趟列车加速到 后, 运行 就前进了 .” 你认为这个说法正确吗?
解答思考
根据问题 1 的条件, 我们不能判断列车以 运行半小时后的情况, 所以上述说法不正确. 显然, 其原因是没有关注到 的变化范围.
问题 1 续
下面用更精确的语言表示问题 1 中 与 的对应关系.
列车行进的路程 与运行时间 的对应关系是
其中, 的变化范围是数集 的变化范围是数集 .对于数集 中的任一时刻 , 按照对应关系(1), 在数集 中都有唯一确定的路程 和它对应.
问题 2
某电气维修公司要求工人每周工作至少 1 天, 至多 6 天. 如果公司确定的工资标准是每人每天 350 元, 而且每周付一次工资, 那么你认为该怎样确定一个工人每周的工资? 一个工人的工资 (单位: 元) 是他工作天数 的函数吗?
显然, 工资 是一周工作天数 的函数, 其对应关系是
其中, 的变化范围是数集 的变化范围是数集 . 对于数集 中的任一个工作天数 , 按照对应关系(2), 在数集 中都有唯一确定的工资 与它对应.
思考
问题 1 和问题 2 中的函数有相同的对应关系,你认为它们是同一个函数吗? 为什么?
问题 3
图 3.1-1 是北京市 2016 年 11 月 23 日的空气质量指数(Air Quality Index, 简称 AQI)变化图. 如何根据该图确定这一天内任一时刻 的空气质量指数 (AQI) 的值 ? 你认为这里的 是 的函数吗?

从图 3.1-1 中的曲线可知, 的变化范围是数集 , AQI 的值 都在数集 中. 对于数集 中的任一时刻 , 按照图 3.1-1 中曲线所给定的对应关系, 在数集 中都有唯一确定的 AQI 的值 与之对应. 因此, 这里的 是 的函数.
思考
你能根据图 3.1-1 找到中午 12 时的 的值吗?
问题 4
国际上常用恩格尔系数 100%) 反映一个地区人民生活质量的高低, 恩格尔系数越低,生活质量越高. 表 3.1-1 是我国某省城镇居民恩格尔系数变化情况, 从中可以看出, 该省城镇居民的生活质量越来越高.
表 3.1-1 我国某省城镇居民恩格尔系数变化情况
| 年份 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|---|---|---|---|---|
| 恩格尔系数 | 36.69 | 36.81 | 38.17 | 35.69 | 35.15 | 33.53 | 33.87 | 29.89 | 29.35 | 28.57 |
你认为按表 3.1-1 给出的对应关系, 恩格尔系数 是年份 的函数吗? 如果是, 你会用怎样的语言来刻画这个函数?
这里, 的取值范围是数集 , ; 根据恩格尔系数的定义可知, 的取值范围是数集 . 对于数集 中的任意一个年份 , 根据表 3.1-1 所给定的对应关系, 在数集 中都有唯一确定的恩格尔系数 与之对应. 所以, 是 的函数.
归纳
上述问题 问题 4 中的函数有哪些共同特征? 由此你能概括出函数概念的本质特征吗?
解
上述问题的共同特征有:
(1) 都包含两个非空数集,用 来表示;
(2) 都有一个对应关系;
(3) 尽管对应关系的表示方法不同,但它们都有如下特性:对于数集 中的任意一个数 , 按照对应关系, 在数集 中都有唯一确定的数 和它对应.
事实上, 除解析式、图象、表格外, 还有其他表示对应关系的方法. 为了表示方便,我们引进符号 统一表示对应关系.
定义 函数
一般地, 设 是非空的实数集, 如果对于集合 中的任意一个数 , 按照某种确定的对应关系 , 在集合 中都有唯一确定的数 和它对应, 那么就称 为从集合 到集合 的一个函数(function),记作
其中, 叫做自变量, 的取值范围 叫做函数的定义域 (domain); 与 的值相对应的 值叫做函数值, 函数值的集合 叫做函数的值域 (range).
17 世纪后期, 德国数学家莱布尼茨第一次将 “function”一词作为专门的数学术语; 19 世纪, 李善兰首次将 function 翻译成 “函数”.
例子
显然, 值域是集合 的子集. 在问题 1 与问题 2 中, 值域就是 和 ; 在问题 3 中, 值域是数集 的真子集;在问题 4 中, 值域 , , 是数集 的真子集.
例子
我们所熟悉的一次函数 的定义域是 , 值域也是 . 对应关系 把 中的任意一个数 , 对应到 中唯一确定的数 .
例子
二次函数 的定义域是 , 值域是 . 当 时, ; 当 时, . 对应关系 把 中的任意一个数 , 对应到 中唯一确定的数 .
思考
反比例函数 的定义域、对应关系和值域各是什么? 请用函数定义描述这个函数.
例 1
函数的解析式是舍弃问题的实际背景而抽象出来的, 它所反映的两个量之间的对应关系, 可以广泛地用于刻画一类事物中的变量关系和规律. 例如, 正比例函数 可以用来刻画匀速运动中路程与时间的关系、一定密度的物体的质量与体积的关系、圆的周长与半径的关系等.
试构建一个问题情境, 使其中的变量关系可以用解析式 来描述.
解:
把 看成二次函数, 那么它的定义域是 , 值域是 .对应关系 把 中的任意一个数 , 对应到 中唯一确定的数 .
如果对 的取值范围作出限制, 例如 , 那么可以构建如下情境:
长方形的周长为 20 , 设一边长为 , 面积为 , 那么 .
其中, 的取值范围是 的取值范围是 . 对应关系 把每一个长方形的边长 , 对应到唯一确定的面积 .
探究
构建其他可用解析式 描述其中变量关系的问题情境.
练习
1.
一枚炮弹发射后, 经过 落到地面击中目标. 炮弹的射高为 , 且炮弹距地面的高度 (单位: )与时间 (单位: ) 的关系为
求(1)所表示的函数的定义域与值域, 并用函数的定义描述这个函数.
2.
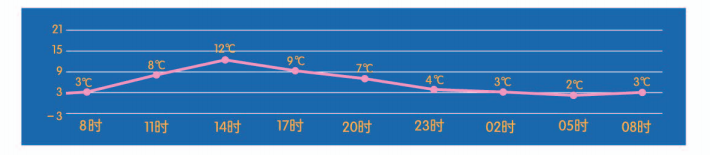
2016 年 11 月 2 日 8 时至次日 8 时(次日的时间前加 0 表示)北京的温度走势如图所示.
(1) 求对应关系为图中曲线的函数的定义域与值域;
(2) 根据图象, 求这一天 12 时所对应的温度.
3.
集合 与对应关系 如下图所示:

是否为从集合 到集合 的函数? 如果是, 那么定义域、值域与对应关系各是什么?
4.
构建一个问题情境, 使其中的变量关系能用解析式 来描述.
定义
研究函数时常会用到区间的概念.
设 是两个实数, 而且 . 我们规定:
(1) 满足不等式 的实数 的集合叫做闭区间, 表示为 ;
(2) 满足不等式 的实数 的集合叫做开区间, 表示为 ;
(3) 满足不等式 或 的实数 的集合叫做半开半闭区间, 分别表示为 .
这里的实数 与 都叫做相应区间的端点.
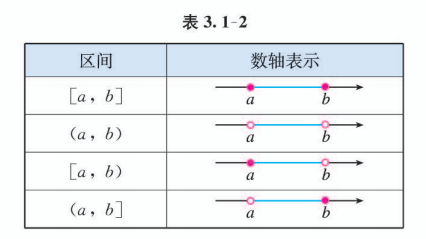
这些区间的几何表示如表 3.1-2 所示. 在数轴表示时, 用实心点表示包括在区间内的端点, 用空心点表示不包括在区间内的端点.
实数集 可以用区间表示为 , “ ” 读作 “无穷大”, “ ” 读作 “负无穷大”, “ ” 读作 “正无穷大”.
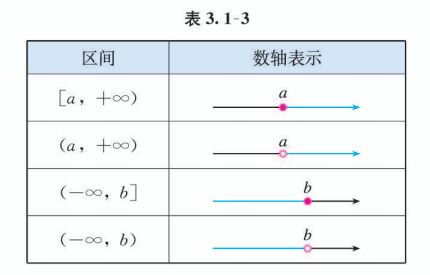
满足 的实数 的集合, 可以用区间分别表示为 . 这些区间的几何表示如表 3.1-3 所示.
在函数定义中, 我们用符号 表示函数, 其中 表示 对应的函数值, 而不是 乘 .
例 2
已知函数 ,
(1) 求函数的定义域;
(2) 求 的值;
(3) 当 时, 求 的值.
分析:
函数的定义域通常由问题的实际背景确定. 如果只给出解析式 , 而没有指明它的定义域, 那么函数的定义域就是指能使这个式子有意义的实数的集合.
解:
(1) 使根式 有意义的实数 的集合是 , 使分式 有意义的实数 的集合是 . 所以, 这个函数的定义域是
即.
(2) 将 -3 与 代人解析式, 有
(3) 因为 , 所以 有意义.
定理 同一个函数
由函数的定义可知, 一个函数的构成要素为: 定义域、对应关系和值域. 因为值域是由定义域和对应关系决定的, 所以, 如果两个函数的定义域相同, 并且对应关系完全一致, 即相同的自变量对应的函数值也相同, 那么这两个函数是同一个函数.
例子
两个函数如果仅有对应关系相同, 但定义域不相同, 那么它们不是同一个函数. 例如, 前面的问题 1 和问题 2 中, 尽管两个函数的对应关系都是 , 但它们的定义域不相同, 因此它们不是同一个函数; 同时, 它们的定义域都不是 , 而是 的真子集,因此它们与正比例函数 也不是同一个函数.
例子
此外, 函数 与 , , 虽然表示它们的字母不同, 但因为它们的对应关系和定义域相同, 所以它们是同一个函数.
例 3
下列函数中哪个与函数 是同一个函数?
(1) ;
(2) ;
(3) ;
(4) .
解:
(1) , 它与函数 虽然对应关系相同, 但是定义域不相同, 所以这个函数与函数 不是同一个函数.
(2) , 它与函数 不仅对应关系相同, 而且定义域也相同, 所以这个函数与函数 是同一个函数.
(3) 它与函数 的定义域都是实数集 , 但是当 时, 它的对应关系与函数 不相同. 所以这个函数与函数 不是同一个函数.
(4) , 它与函数 的对应关系相同但定义域不相同. 所以这个函数与函数 不是同一个函数.
也可以利用信息技术画出例 3 中四个函数的图象, 根据图象进行判断.
思考
至此, 我们在初中学习的基础上, 运用集合语言和对应关系刻画了函数, 并引进了符号 , 明确了函数的构成要素. 比较函数的这两种定义, 你对函数有什么新的认识?
练习
1.
求下列函数的定义域:
(1) ;
(2) .
2.
已知函数 ,
(1) 求 的值;
(2) 求 的值.
3.
判断下列各组中的函数是否为同一个函数, 并说明理由:
(1) 表示炮弹飞行高度 与时间 关系的函数 和二次函数 ;
(2) 和 .
3.1.2 函数的表示法
函数表示法
我们在初中已经接触过函数的三种表示法: 解析法、列表法和图象法.
解析法, 就是用解析式表示两个变量之间的对应关系, 如 3.1.1 的问题 1、2.
列表法, 就是列出表格来表示两个变量之间的对应关系, 如 3.1.1 的问题 4.
图象法, 就是用图象表示两个变量之间的对应关系, 如 3.1.1 的问题 3.
这三种方法是常用的函数表示法.
例 4
某种笔记本的单价是 5 元, 买 个笔记本需要 元. 试用函数的三种表示法表示函数 .
解:
这个函数的定义域是数集 .
用解析法可将函数 表示为
用列表法可将函数 表示为
| 笔记本数 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 钱数 | 5 | 10 | 15 | 20 | 25 |
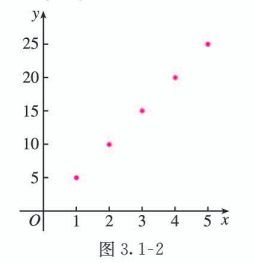
用图象法可将函数 表示为图 3.1-2.
思考
函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.那么判断一个图形是不是函数图象的依据是什么?
思考
(1) 比较函数的三种表示法,它们各自的特点是什么?
(2) 所有函数都能用解析法表示吗? 请你举出实例加以说明.
例 5
画出函数 的图象.
解:
由绝对值的概念, 我们有
所以, 函数 的图象如图 3.1-3 所示.
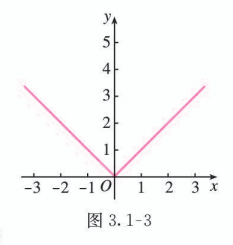
定义 分段函数
像例 5 中 这样的函数称为分段函数. 生活中, 有很多可以用分段函数描述的实际问题, 如出租车的计费、个人所得税纳税额等.
例 6
给定函数 ,
(1) 在同一直角坐标系中画出函数 的图象;
(2) , 用 表示 中的最大者, 记为
例如, 当 时, .
请分别用图象法和解析法表示函数 .
解:
(1) 在同一直角坐标系中画出函数 的图象 (图 3.1-4).

(2) 由图 3.1-4 中函数取值的情况,结合函数 的定义,可得函数 的图象 (图 3.1-5).
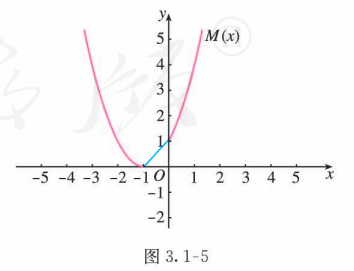
由 , 得 .
解得 , 或 .
结合图 3.1-5, 得出函数 的解析式为
思考
你能用其他方法求出 的解析式吗?
练习
1.
如图, 把直截面半径为 的圆柱形木头锯成直截面为矩形的木料, 如果矩形的一边长为 (单位: ), 面积为 (单位: ), 把 表示为 的函数.

2.
画出函数 的图象.
3.
给定函数 ,
(1) 画出函数 的图象;
(2) , 用 表示 中的最小者, 记为 , 请分别用图象法和解析法表示函数 .
对于一个具体的问题, 如果涉及函数, 那么应当学会选择恰当的方法表示问题中的函数关系.
例 7
表 3.1-4 是某校高一 (1) 班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
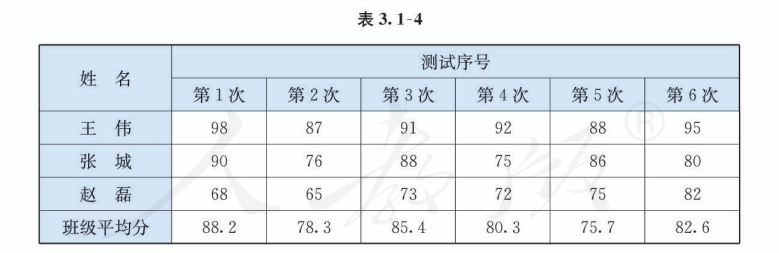
请你对这三位同学在高一学年的数学学习情况做一个分析.
解:
从表 3.1-4 中可以知道每位同学在每次测试中的成绩, 但不太容易分析每位同学的成绩变化情况. 如果将每位同学的 “成绩” 与 “测试序号” 之间的函数关系分别用图象 (均为 6 个离散的点) 表示出来, 如图 3.1-6, 那么就能直观地看到每位同学成绩变化的情况, 这对我们的分析很有帮助.
从图 3.1-6 可以看到, 王伟同学的数学学习成绩始终高于班级平均水平, 学习情况比较稳定而且成绩优秀. 张城同学的数学学习成绩不稳定, 总是在班级平均水平上下波动, 而且波动幅度较大. 赵磊同学的数学学习成绩低于班级平均水平, 但表示他成绩变化的图象呈上升趋势, 表明他的数学成绩在稳步提高.
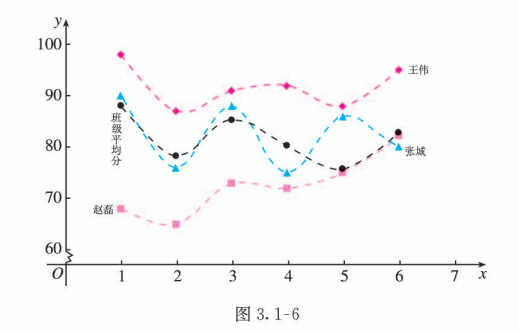
为了更容易看出一个同学的学习情况, 我们将表示每位同学成绩的函数图象 (离散的点) 用虚线连接.
例 8
依法纳税是每个公民应尽的义务, 个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税). 2019 年 1 月 1 日起, 个税税额根据应纳税所得额、税率和速算扣除数确定, 计算公式为
应纳税所得额的计算公式为
其中, “综合所得” 包括工资、薪金, 劳务报酬, 稿酬, 特许权使用费; “专项扣除” 包括居民个人按照国家规定的范围和标准缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金等; “专项附加扣除” 包括子女教育、继续教育、大病医疗、住房货款利息或者住房租金、赡养老人等支出; “其他扣除” 是指除上述基本减除费用、专项扣除、专项附加扣除之外, 由国务院决定以扣除方式减少纳税的优惠政策规定的费用.
其中, “基本减除费用” (免征额) 为每年 60000 元. 税率与速算扣除数见表 3.1-5.
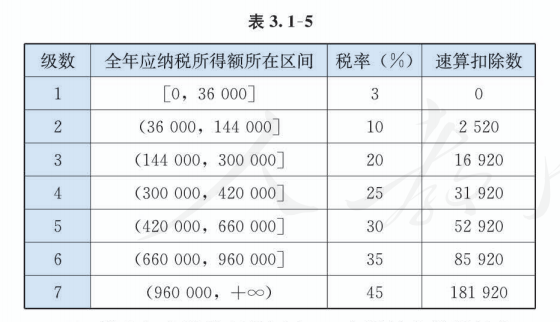
(1) 设全年应纳税所得额为 , 应缴纳个税税额为 ,求 , 并画出图象;
(2) 小王全年综合所得收人额为 117600 元, 假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收人额的比例分别是 , 专项附加扣除是 9600 元, 依法确定其他扣除是 560 元, 那么他全年应缴纳多少综合所得个税?
分析:
根据个税产生办法, 可按下列步骤计算应缴纳个税税额:
第一步, 根据 ② 计算出应纳税所得额 ;
第二步, 由 的值并根据表 3.1-5 得出相应的税率与速算扣除数;
第三步, 根据 ① 计算出个税税额 的值.
由于不同应纳税所得额 对应不同的税率与速算扣除数, 所以 是 的分段函数.
解:
(1) 根据表 3.1-5, 可得函数 的解析式为
函数图象如图 3.1-7 所示.

(2) 根据 ②, 小王全年应纳税所得额为
将 的值代人 ③, 得
所以, 小王应缴纳的综合所得个税税额为 717.6 元.
练习
1.
下图中哪几个图象与下述三件事分别吻合得最好? 请你为剩下的那个图象写出一件事.
(1) 我离开家不久, 发现自己把作业本忘在家里了, 于是返回家里找到了作业本再上学;
(2) 我骑着车离开家后一路匀速行驶, 只是在途中遇到一次交通堵塞, 耽搁了一些时间;
(3) 我从家出发后, 心情轻松, 一路缓缓加速行进.

2.
某市 “招手即停” 公共汽车的票价按下列规则制定:
(1) 以内 (含 ), 票价 2 元;
(2) 以上, 每增加 , 票价增加 1 元 (不足 的按 计算).
如果某条线路的总里程为 , 请根据题意, 写出票价与里程之间的函数解析式, 并画出函数的图象.
习题 3.1
复习巩固
1.
求下列函数的定义域:
(1) ;
(2) ;
(3) ;
(4) .
2.
下列哪一组中的函数 与 是同一个函数?
(1) ;
(2) ;
(3) .
3.
画出下列函数的图象, 并说出函数的定义域、值域:
(1) ;
(2) ;
(3) ;
(4) .
4.
已知函数 , 求 的值.
5.
已知函数 ,
(1) 点 在 的图象上吗?
(2) 当 时, 求 的值.
(3) 当 时, 求 的值.
6.
若 , 且 , 求 的值.
7.
画出下列函数的图象:
(1)
(2) .
综合运用
8.
如图, 矩形的面积为 10 . 如果矩形的长为 , 宽为 , 对角线为 , 周长为 , 那么你能获得关于这些量的哪些函数?

9.
一个圆柱形容器的底部直径是 , 高是 . 现在向容器内每秒注人某种溶液 . 求容器内溶液的高度 (单位: ) 关于注入溶液的时间 (单位: ) 的函数解析式, 并写出函数的定义域和值域.
10.
一个老师用 5 分制对数学作业评分. 一次作业中, 第一小组同学按座位序号 的次序, 得分依次是 . 你会怎样表示这次作业的得分情况? 用 分别表示序号和对应的得分, 是 的函数吗? 如果是, 那么它的定义域、值域和对应关系各是什么?
11.
函数 的图象如图所示,
(1) 函数 的定义域、值域各是什么?
(2) 取何值时, 只有唯一的 值与之对应?
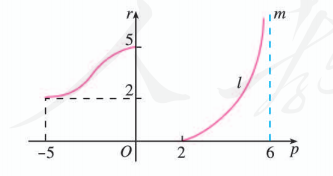
图中, 曲线 与直线 无限接近, 但永不相交.
12.
画出定义域为 , 且 , 值域为 的一个函数的图象.
(1) 将你的图象和其他同学的相比较, 有什么差别吗?
(2) 如果平面直角坐标系中点 的坐标满足 , 那么其中哪些点不能在图象上?
13.
函数 的函数值表示不超过 的最大整数, 例如, . 当 时, 写出函数 的解析式, 并画出函数的图象.
14.
构建一个问题情境, 使其中的变量关系能用解析式 来描述.
拓广探索
15.
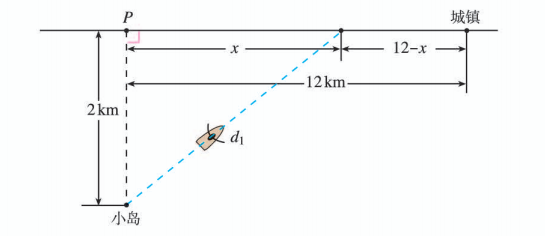
如图所示, 一座小岛距离海岸线上最近的点 的距离是 , 从点 沿海岸正东 处有一个城镇.
(1) 假设一个人驾驶的小船的平均速度为 , 步行的速度是 , (单位: h) 表示他从小岛到城镇的时间, (单位: ) 表示此人将船停在海岸处距点 的距离. 请将 表示为 的函数.
(2) 如果将船停在距点 处, 那么从小岛到城镇要多长时间(精确到 )?
16.
给定数集 , 方程
(1) 任给 , 对应关系 使方程 ① 的解 与 对应, 判断 是否为函数;
(2) 任给 , 对应关系 使方程 ① 的解 与 对应, 判断 是否为函数.
17.
探究是否存在函数 满足条件:
(1) 定义域相同, 值域相同,但对应关系不同;
(2) 值域相同, 对应关系相同,但定义域不同.
18.
在一个展现人脑智力的综艺节目中, 一位参加节目的少年能将圆周率 准确地记忆到小数点后面 200 位, 更神奇的是, 当主持人说出小数点后面的位数时, 这位少年都能准确地说出该数位上的数字. 如果记圆周率 小数点后第 位上的数字为 , 那么你认为 是 的函数吗?如果是, 请写出函数的定义域、值域与对应关系; 如果不是, 请说明理由.
阅读与思考:函数概念的发展历程
17 世纪, 科学家们致力于运动的研究, 如计算天体的位置, 远距离航海中对经度和纬度的测量, 炮弹的速度对于高度和射程的影响等. 诸如此类的问题都需要探究两个变量之间的关系, 并根据这种关系对事物的变化规律作出判断, 如根据炮弹的发射角和初速度推测它能达到的高度和射程. 这正是函数概念产生和发展的背景.
“function”一词最初由德国数学家莱布尼茨 (G. W. Leibniz,1646-1716)使用. 在中国, 清代数学家李善兰 (1811-1882) 在 1859 年和英国传教士伟烈亚力合译的《代微积拾级》中首次将 “function” 译作 “函数”.
莱布尼茨用 “函数” 表示随曲线的变化而改变的几何量, 如坐标、切线等. 1718 年, 他的学生、瑞士数学家约翰 伯努利 (J. Bernoulli,1667-1748)强调函数要用式子表示. 后来, 数学家认为这不是判断函数的标准. 只要一些变量变化, 另一些变量随之变化就可以了. 所以, 1755 年,瑞士数学家欧拉 (L. Euler, 1707-1783) 将函数定义为 “如果某些变量, 以一种方式依赖于另一些变量, 我们将前面的变量称为后面变量的函数”.
当时很多数学家对于不用式子表示函数很不习惯, 甚至抱怀疑态度. 函数的概念仍然是比较模糊的.
随着对微积分研究的深入, 18 世纪末 19 世纪初, 人们对函数的认识向前推进了. 德国数学家狄利克雷 (P. G. L. Dirichlet, 1805-1859) 在 1837 年时提出: “如果对于 的每一个值, 总有一个完全确定的值与之对应, 那么 是 的函数.” 这个定义较清楚地说明了函数的内涵. 只要有一个法则, 使得取值范围中的每一个 , 有一个确定的 和它对应就行了, 不管这个法则是用解析式还是用图象、表格等形式表示. 例如, 狄利克雷函数, 即: 当自变量取有理数时, 函数值为 1 ; 当自变量取无理数时, 函数值为 0 . 它只能用对应的语言予以表达. 19 世纪 70 年代以后, 随着集合概念的出现, 函数概念又进而用更加严谨的集合和对应语言表述, 这就是本节学习的函数概念.
综上所述可知, 函数概念的发展与生产、生活以及科学技术的实际需要紧密相关, 而且随着研究的深入, 函数概念不断得到严谨化、精确化的表达, 这与我们学习函数的过程是一样的.
你能以函数概念的发展为背景, 谈谈从初中到高中学习函数概念的体会吗?