4.6 小结
2024-03-02 22:34:55 新建
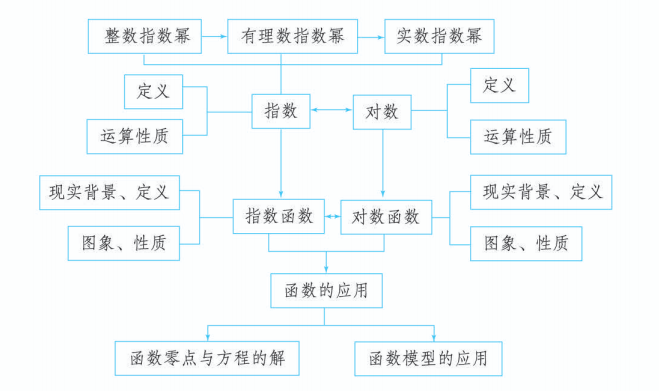
本章知识结构
回顾与思考
本章我们先将指数概念由整数指数逐步拓展到了实数指数, 并给出了实数指数幂的运算法则; 通过对指数增长方式的实例分析, 引入指数函数的概念,并研究了它的图象和性质. 从对数与指数的相互联系出发, 引入对数的概念,研究了对数的运算法则; 在此基础上研究了对数函数的概念、图象和性质. 指数函数和对数函数是两种不同类型但联系紧密的函数模型, 是刻画客观世界中 “指数爆炸” “对数增长” 现象的重要数学模型. 利用函数零点与方程解之间的关系, 我们引入了函数零点存在定理, 探索了用二分法求方程近似解的思路.二分法是求方程近似解的一般性方法. 不同类型的函数具有不同的增长方式,通过比较, 我们认识了对数函数、线性函数、指数函数增长速度的差异, 并通过具体实例, 学习了如何根据增长速度的差异, 选择合适的函数类型构建数学模型、刻画现实问题变化规律的方法.
本章中, 先从整数指数拓展到有理数指数, 再利用有理数指数幂逼近无理数指数幂的思想认识无理数指数幂, 从而将指数的概念拓展到实数指数; 通过问题 “在 , 且 中, 已知 求 ” 引入, 按照 “定义——表示——性质——运算 (法则) ——应用” 的路径研究对数. 这里要注意体会数学概念推广的基本思想. 整体而言, 对指数函数、对数函数的研究, 都是按照 “实际问题——函数概念——图象与性质——应用” 的路径展开. 这里要特别注意在对现实问题增长方式分析的基础上引入相应的函数概念, 再通过对函数图象、性质的研究, 把握相应函数的本质. 这是建立函数模型解决实际问题的基础.
在应用函数解决实际问题时, 首先应注意分析实际问题属于哪种类型的增长方式, 这是选择和建立函数模型的基础; 其次, 要注意理解用函数构建数学模型的基本过程, 体会运用模型思想发现和提出问题、分析和解决问题的数学方法.
请你带着下面的问题, 复习一下全章内容吧!
- 指数和对数的概念都有现实背景, 你能举出一些实际例子吗?
- 概述指数概念的拓展过程, 你能由此说说数学概念拓展的过程与方法吗?
- 对数概念是如何提出来的? 它对发现和提出问题有什么启示?
- 回忆指数函数、对数函数的研究过程, 你能由此说说如何研究一类函数吗? 例如研究的内容、过程和方法.
- 不同函数模型刻画了现实世界不同类型问题的变化规律, 你能说说指数函数和对数函数分别刻画了怎样的变化规律吗?你能举出 “直线上升” “对数增长” “指数爆炸” 的实际例子吗?
- 你能举例说明函数的零点与方程解的关系吗? 在什么条件下, 函数在 内一定有零点?
- 你能说说用二分法求方程近似解的一般步骤吗?
- 你能结合实例说明应用函数模型解决问题的基本过程吗?
- 函数图象是研究函数性质的重要载体, 信息技术是研究函数图象与性质的有力工具, 你能结合实例谈谈这方面的体会吗?
复习参考题 4
复习巩固
1.
选择题
(1) 函数 与 的图象 ( ).
(A) 关于 轴对称
(B) 关于 轴对称
© 关于原点对称
(D) 关于直线 对称
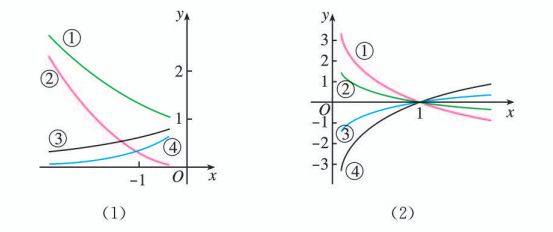
(2) 如图 (1), ① ② ③ ④ 中不属于函数 的一个是 ( ).
(A) ① (B) ② © ③ (D) ④
(3) 如图 (2), ① ② ③ ④ 中不属于函数 的一个是( ),
(A) ① (B) ② © ③ (D) ④
2.
用 “<" “>” “=” 填空:
(1) _ _ _ ;
(2) _ _ _ ;
(3) _ _ _ ;
(4) _ _ _ ;
(5) _ _ _ ;
(6) _ _ _ .
3.
借助信息技术, 用二分法求:
(1) 方程 的最大的根(精确度为 0.01 );
(2) 函数 和 交点的横坐标(精确度为 0.1 ).
4.
已知函数 求使方程 的实数解个数分别为 时 的相应取值范围.
综合运用
5.
选择题
(1) 已知集合 , 则 .
(A)
(B)
©
(D)
(2) 已知 , 若 , 则 ( ).
(A)
(B)
©
(D)
(3) 已知函数 的零点分别为 , 则 , 的大小顺序为 ( ).
(A)
(B)
©
(D)
6.
设 , 求证:
(1) ;
(2) ;
(3) .
7.
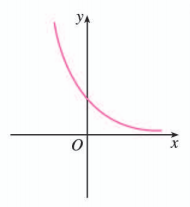
指数函数 的图象如图所示, 求二次函数 图象顶点的横坐标的取值范围.
8.
1986 年 4 月 26 日, 乌克兰境内的切尔诺贝利核电站爆炸, 核泄漏导致事故所在地被严重污染. 主要的核污染物是锶 90 , 它每年的衰减率为 . 专家估计, 要完全消除这次核事故对自然环境的影响至少需要 800 年, 到那时原有的锶 90 还剩百分之几?
9.
某工厂产生的废气经过滤后排放, 过滤过程中废气的污染物含量 (单位: ) 与时间 (单位: ) 间的关系为
其中 是正的常数. 如果在前 消除了 的污染物, 那么
(1) 后还剩百分之几的污染物?
(2) 污染物减少 需要花多少时间(精确到 )?
(3) 画出 关于 变化的函数图象.
10.
把物体放在冷空气中冷却, 如果物体原来的温度是 , 空气的温度是 , 那么 后物体的温度 (单位: ) 可由公式
求得, 其中 是一个随着物体与空气的接触状况而定的正常数. 现有 的物体, 放在 的空气中冷却, 以后物体的温度是 .
(1) 求 的值(精确到 0.01 );
(2) 若要将物体的温度降为 , 求分别需要冷却的时间 (精确到 ).
拓广探索
11.
已知函数 , 且 ,
(1) 求函数 的定义域;
(2) 判断函数 的奇偶性, 并说明理由.
12.
对于函数 ,
(1) 探索函数 的单调性;
(2) 是否存在实数 使函数 为奇函数?
13.
如图, 函数 的图象由曲线段 和直线段 构成.
(1) 写出函数 的一个解析式;
(2) 提出一个能满足函数 图象变化规律的实际问题.
