5.1 任意角和弧度制
2024-03-07 22:28:15 新建
探究
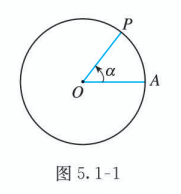
圆周运动是一种常见的周期性变化现象. 如图 5.1-1, 上的点 以 为起点做逆时针方向的旋转. 如何刻画点 的位置变化呢?
解
我们知道, 角可以看成一条射线绕着它的端点旋转所成的图形. 在图 5.1-1 中, 射线的端点是圆心 , 它从起始位置 按逆时针方向旋转到终止位置 , 形成一个角 ,射线 分别是角 的始边和终边. 当角 确定时,终边 的位置就确定了. 这时, 射线 与 的交点 也就确定了. 由此想到, 可以借助角 的大小变化刻画点 的位置变化.
由初中知识可知, 射线 绕端点 按逆时针方向旋转一周回到起始位置, 在这个过程中可以得到 范围内的角. 如果继续旋转, 那么所得到的角就超出这个范围了. 所以, 为了借助角的大小变化刻画圆周运动, 需要先扩大角的范围.
5.1.1 任意角
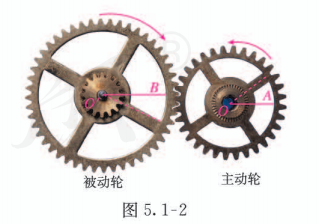
现实生活中随处可见超出 范围的角. 例如,体操中有 “前空翻转体 540 度” “后空翻转体 720 度” 这样的动作名称, 这里不仅有超出 范围的角, 而且旋转的方向也不相同; 又如, 图 5.1-2 是两个齿轮旋转的示意图, 被动轮随着主动轮的旋转而旋转, 而且被动轮与主动轮有相反的旋转方向. 这样, 绕点 旋转所成的角与 绕点 旋转所成的角就会有不同的方向. 因此, 要准确地描述这些现象, 不仅要知道旋转的度数, 还要知道旋转的方向, 这就需要对角的概念进行推广.
为了简单起见, 在不引起混淆的前提下, “角 ” 或 “ ” 可以简记成 “ ".
定义 正角 负角 零角
我们规定,
一条射线绕其端点按逆时针方向旋转形成的角叫做正角,
按顺时针方向旋转形成的角叫做负角.
如果一条射线没有做任何旋转, 就称它形成了一个零角.
这样, 零角的始边与终边重合. 如果 是零角, 那么 .
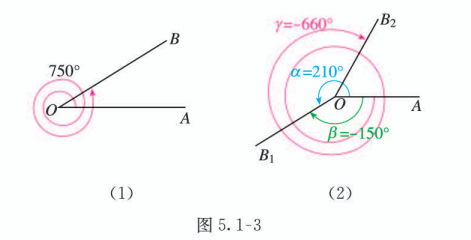
例子 正角 负角 零角
图 5.1-3(1) 中的角是一个正角, 它等于 750 ; 图 5.1-3(2) 中, 正角 , 负角 . 正常情况下, 如果以零时为起始位置, 那么钟表的时针或分针在旋转时所形成的角总是负角.
定义 任意角 相等角
这样, 我们就把角的概念推广到了任意角, 包括正角、负角和零角. 设角 由射线 绕端点 旋转而成, 角 由射线 绕端点 旋转而成. 如果它们的旋转方向相同且旋转量相等, 那么就称 .
定义 角的加法 角的减法
设 是任意两个角.
我们规定, 把角 的终边旋转角 , 这时终边所对应的角是 .
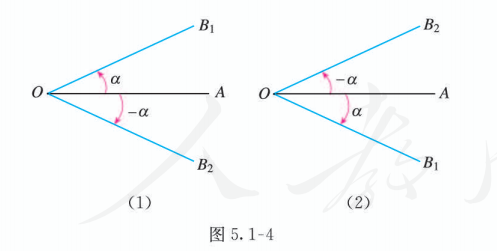
类似于实数 的相反数是 , 我们引入任意角 的相反角的概念. 如图 5.1-4, 我们把射线 绕端点 按不同方向旋转相同的量所成的两个角叫做互为相反角. 角 的相反角记为 . 于是, 像实数减法的 “减去一个数等于加上这个数的相反数” 一样, 我们有
这样, 角的减法可以转化为角的加法.
定义 第几象限角
我们通常在直角坐标系内讨论角. 为了方便, 使角的顶点与原点重合, 角的始边与 轴的非负半轴重合.那么, 角的终边在第几象限, 就说这个角是第几象限角.
例子
例如, 图 5.1-5 中的 角、 角分别是第一象限角和第三象限角. 如果角的终边在坐标轴上, 那么就认为这个角不属于任何一个象限.
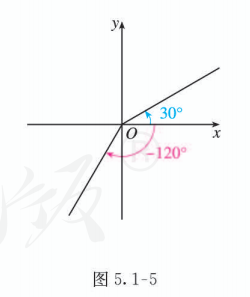
思考
你能说说在直角坐标系内讨论角的好处吗?
探究
将角按照上述方法放在直角坐标系中后, 给定一个角,就有唯一的一条终边与之对应. 反之, 对于直角坐标系内任意一条射线 (图 5.1-6), 以它为终边的角是否唯一? 如果不唯一, 那么终边相同的角有什么关系?
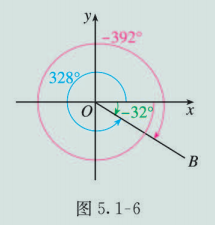
解
不难发现, 在图 5.1-6 中, 如果 角的终边是 , 那么 角的终边都是 , 并且与 角终边相同的这些角都可以表示成 的角与 个 周角的和, 如
设 , 则 角都是 的元素, 角也是 的元素 (此时 ). 因此, 所有与 角终边相同的角, 连同 角在内, 都是集合 的元素; 反过来, 集合 的任一元素显然与 角的终边相同.
任一与角 终边相同的角
一般地, 我们有:
所有与角 终边相同的角, 连同角 在内, 可构成一个集合
即任一与角 终边相同的角, 都可以表示成角 与整数个周角的和.
在直角坐标系中, 角的终边绕原点旋转 后回到原来的位置. 因此,在直角坐标系中讨论角可以很好地表现角的 “周而复始” 的变化规律.
例 1
在 范围内, 找出与 角终边相同的角, 并判定它是第几象限角.
解:
, 所以在 范围内, 与一 角终边相同的角是 , 它是第二象限角.
例 2
写出终边在 轴上的角的集合.
解:
在 范围内, 终边在 轴上的角有两个, 即 角 (图 5.1-7).
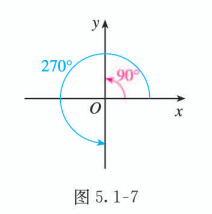
因此, 所有与 角终边相同的角构成集合
而所有与 角终边相同的角构成集合
于是, 终边在 轴上的角的集合
例 3
写出终边在直线 上的角的集合 中满足不等式 的元素 有哪些?
解:
如图 5.1-8, 在直角坐标系中画出直线 , 可以发现它与 轴的夹角是 , 在 范围内, 终边在直线 上的角有两个: .
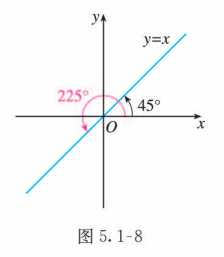
因此, 终边在直线 上的角的集合
中适合不等式 的元素 有
练习
1.
(口答) 锐角是第几象限角? 第一象限角一定是锐角吗? 再分别就直角、钝角来回答这两个问题.
2.
(口答) 今天是星期三, 那么 天后的那一天是星期几? 天前的那一天是星期几? 100 天后的那一天是星期几?
3.
已知角的顶点与直角坐标系的原点重合, 始边与 轴的非负半轴重合, 作出下列各角, 并指出它们是第几象限角 :
(1) ;
(2) ;
(3) ;
(4) .
4.
在 范围内, 找出与下列各角终边相同的角, 并指出它们是第几象限角:
(1) ;
(2) ;
(3) .
5.
写出与下列各角终边相同的角的集合, 并找出集合中适合不等式 的元素 :
(1) ;
(2) .
5.1.2 弧度制
探究
度量长度可以用米、英尺、码等不同的单位制, 度量质量可以用千克、磅等不同的单位制. 不同的单位制能给解决问题带来方便. 角的度量是否也能用不同的单位制呢? 能否像度量长度那样, 用十进制的实数来度量角的大小呢?
定义 角度制
我们知道, 角可以用度为单位进行度量, 1 度的角等于周角的 . 这种用度作为单位来度量角的单位制叫做角度制.
下面介绍在数学和其他科学研究中经常采用的另一种度量角的单位制——弧度制.
探究
如图 5.1-9, 射线 绕端点 旋转到 形成角 . 在旋转过程中, 射线 上的一点 (不同于点 ) 的轨迹是一条圆弧,这条圆弧对应于圆心角 .
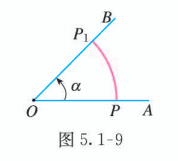
设 , 点 所形成的圆弧 的长为 . 由初中所学知识可知 , 于是
如图 5.1-10, 在射线 上任取一点 (不同于点 ), . 在旋转过程中, 点 所形成的圆弧 的长为 . 与 的比值是多少? 你能得出什么结论?
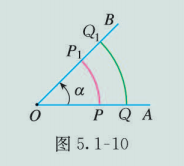
解
可以发现, 圆心角 所对的弧长与半径的比值, 只与 的大小有关. 也就是说, 这个比值随 的确定而唯一确定.这就启发我们, 可以利用圆的弧长与半径的关系度量圆心角.
定义 弧度制
我们规定: 长度等于半径长的圆弧所对的圆心角叫做 1 弧度(radian)的角, 弧度单位用符号 rad 表示, 读作弧度.
我们把半径为 1 的圆叫做单位圆. 如图 5.1-11, 在单位圆 中, 的长等于 就是 1 弧度的角.
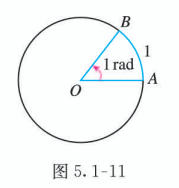
根据上述规定, 在半径为 的圆中, 弧长为 的弧所对的圆心角为 , 那么
其中, 的正负由角 的终边的旋转方向决定, 即逆时针旋转为正, 顺时针旋转为负. 当角的终边旋转一周后继续旋转, 就可以得到弧度数大于 或小于 的角. 这样就可以得到弧度为任意大小的角.
一般地, 正角的弧度数是一个正数, 负角的弧度数是一个负数, 零角的弧度数是 0 .
公元 6 世纪, 印度人在制作正弦表时, 曾用同一单位度量半径和圆周,孕育着最早的弧度制概念.欧拉是明确提出弧度制思想的数学家. 1748 年, 在他的一部划时代著作《无穷小分析概论》中, 提出把圆的半径作为弧长的度量单位, 使一个圆周角等于 弧度, 1 弧度等于周角的 . 这一思想将线段与弧的度量统一起来, 大大简化了三角公式及计算.
探究
角度制、弧度制都是角的度量制, 它们之间应该可以换算.如何换算呢?
解
用角度制和弧度制来度量零角, 单位不同, 但量数相同 (都是 0 ); 用角度制和弧度制度量任一非零角, 单位不同,量数也不同. 因为周角的弧度数是 , 而在角度制下的度数是 360 , 所以
反过来有
一般地, 只需根据
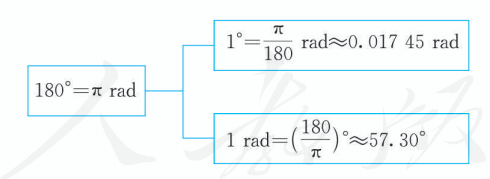
就可以进行弧度与角度的换算了.
例 4
按照下列要求, 把 化成弧度:
(1) 精确值;
(2) 精确到 0.001 的近似值.
解:
(1) 因为 , 所以
(2) 利用计算器有

因此, .
例 5
将 换算成角度(用度数表示, 精确到 0.001 ).
解:
利用计算器有

因此, .
定义 弧度[补充]
今后用弧度制表示角时, “弧度” 二字或 “rad” 通常略去不写, 而只写该角所对应的弧度数.
例子
例如, 角 就表示 是 的角; 就表示 的角的正弦, 即 .
探究
填写下列特殊角的度数与弧度数的对应表:

定理 角的集合与实数集 之间建立起一一对应的关系
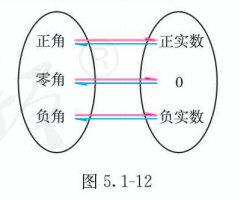
角的概念推广后, 在弧度制下,角的集合与实数集 之间建立起一一对应的关系: 每一个角都有唯一的一个实数(等于这个角的弧度数) 与它对应; 反过来, 每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应 (图 5.1-12).
例 6
利用弧度制证明下列关于扇形的公式:
(1) ;
(2) ;
(3) .
其中 是圆的半径, 为圆心角, 是扇形的弧长, 是扇形的面积.
证明:
由公式 可得
下面证明 (2)(3).
半径为 , 圆心角为 的扇形的弧长公式和面积公式分别是
将 转换为弧度, 得
于是,
将 代人上式, 即得
显然, 弧度制下的弧长公式和扇形面积公式形式简单了. 在今后的学习中, 我们还将进一步看到弧度制带来的便利.
练习
1.
把下列角度化成弧度:
(1) ;
(2) ;
(3) .
2.
把下列弧度化成角度:
(1) ;
(2) ;
(3) .
3.
用弧度表示:
(1) 终边在 轴上的角的集合;
(2) 终边在 轴上的角的集合.
4.
利用计算工具比较下列各对值的大小:
(1) 和 ;
(2) 和 .
5.
分别用角度制、弧度制下的弧长公式, 计算半径为 的圆中, 的圆心角所对的弧的长度 (可用计算工具).
6.
已知半径为 的圆上, 有一条弧的长是 , 求该弧所对的圆心角 (正角) 的弧度数.
习题 5.1
复习巩固
1.
在 范围内, 找出与下列各角终边相同的角, 并指出它们是哪个象限的角:
(1) ;
(2) ;
(3) ;
(4) .
2.
写出与下列各角终边相同的角的集合, 并找出集合中适合不等式 的元素 :
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) ;
(7) ;
(8) .
3.
分别用角度和弧度写出第一、二、三、四象限角的集合.
4.
一条弦的长等于半径, 这条弦所对的圆心角等于 1 弧度吗? 为什么?
5.
把下列角度化成弧度:
(1) ;
(2) ;
(3) ;
(4) .
6.
把下列弧度化成角度 (第 (3) (4) 题精确到 ):
(1) ;
(2) ;
(3) 1.4 ;
(4) .
综合运用
7.
选择题
(1) 已知 是锐角, 那么 是 ( ).
(A) 第一象限角
(B) 第二象限角
© 小于 的正角
(D) 第一或第二象限角
(2) 已知 是第一象限角, 那么 是().
(A) 第一象限角
(B) 第二象限角
© 第一或第二象限角
(D) 第一或第三象限角
8.
要在半径 的圆形金属板上截取一块扇形板, 使其弧 的长为 , 那么圆心角 是多少度 (可用计算工具, 精确到 )?
9.
已知弧长 的弧所对圆心角为 , 求这条弧所在的圆的半径 (可用计算工具, 精确到 ).
拓广探索
10.
每人准备一把扇形的扇子, 然后与本小组其他同学的对比, 从中选出一把展开后看上去形状较为美观的扇子, 并用计算工具算出它的面积 .
(1) 假设这把扇子是从一个圆面中剪下的, 而剩余部分的面积为 , 求 与 的比值;
(2) 要使 与 的比值为 0.618 , 则扇子的圆心角应为几度 (精确到 )?
11.
(1) 时间经过 (时), 时针、分针各转了多少度? 各等于多少弧度?
(2) 有人说, 钟的时针和分针一天内会重合 24 次. 你认为这种说法是否正确? 请说明理由. (提示:从午夜零时算起, 假设分针走了 会与时针重合, 一天内分针和时针会重合 次, 利用分针与时针转动的速度, 建立 关于 的函数解析式, 并求解.)
12.
已知相互啮合的两个齿轮, 大轮有 48 齿, 小轮有 20 齿.
(1) 当大轮转动一周时, 求小轮转动的角度;
(2) 如果大轮的转速为 (转/分), 小轮的半径为 , 那么小轮周上一点每 转过的弧长是多少?