1.3 集合的基本运算
2024-01-03 23:25:56 新建
我们知道, 实数有加、减、乘、除等运算. 集合是否也有类似的运算呢?
并集
观察
观察下面的集合, 类比实数的加法运算, 你能说出集合 与集合 之间的关系吗?
(1) ;
(2) 是有理数 是无理数 是实数 .
在上述两个问题中, 集合 与集合 之间都具有这样一种关系:集合 是由所有属于集合 或属于集合 的元素组成的.
定义
一般地, 由所有属于集合 或属于集合 的元素组成的集合, 称为集合 与 的并集 (union set), 记作 (读作 “ 并 ” ), 即
可用 Venn 图(图 1.3-1)表示.
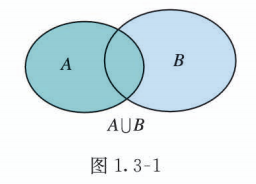
这样, 在问题(1)(2) 中, 集合 与 的并集是 , 即
例 1
设 , 求 .
解:
.
在求两个集合的并集时, 它们的公共元素在并集中只能出现一次. 如元素 5, 8 .
例 2
设集合 , 集合 , 求 .
解:
如图 1.3-2, 还可以利用数轴直观表示例 2 中求并集 的过程.
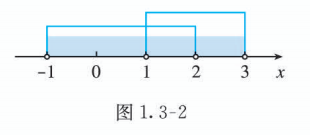
思考
下列关系式成立吗?
(1) ; (2) .
交集
思考
观察下面的集合, 集合 与集合 之间有什么关系?
(1) ;
(2) 是立德中学今年在校的女同学 是立德中学今年在校的高一年级同学 是立德中学今年在校的高一年级女同学 .
在上述两个问题中, 集合 是由所有既属于集合 又属于集合 的元素组成的.
定义
一般地, 由所有属于集合 且属于集合 的元素组成的集合, 称为集合 与 的交集 (intersection set), 记作 (读作 “ 交 ”), 即
可用 Venn 图(图 1.3-3)表示.
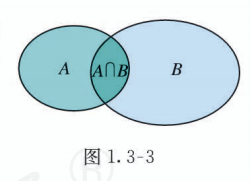
这样, 在上述问题 (1) (2) 中, .
例 3
立德中学开运动会, 设
是立德中学高一年级参加百米赛跑的同学 ,
是立德中学高一年级参加跳高比赛的同学 ,
求 .
解:
就是立德中学高一年级中那些既参加百米赛跑又参加跳高比赛的同学组成的集合. 所以,
是立德中学高一年级既参加百米赛跑又参加跳高比赛的同学 .
例 4
设平面内直线 上点的集合为 , 直线 上点的集合为 , 试用集合的运算表示 的位置关系.
解:
平面内直线 可能有三种位置关系, 即相交于一点、平行或重合.
(1) 直线 相交于一点 可表示为
(2) 直线 平行可表示为
(3) 直线 重合可表示为
思考
下列关系式成立吗?
(1) ; (2) .
练习
1.
设 , 求 .
2.
设 , 求 .
3.
设 是等腰三角形 是直角三角形 , 求 .
4.
设 是幸福农场的汽车 是幸福农场的货车 , 求 .
补集
在研究问题时, 我们经常需要确定研究对象的范围.
例如, 从小学到初中, 数的研究范围逐步地由自然数到正分数, 再到有理数, 引进无理数后, 数的研究范围扩充到实数. 在高中阶段, 数的研究范围将进一步扩充.
在不同范围研究同一个问题, 可能有不同的结果. 例如方程 的解集, 在有理数范围内只有一个解 2 , 即
在实数范围内有三个解: , 即
定义 全集
一般地, 如果一个集合含有所研究问题中涉及的所有元素, 那么就称这个集合为全集 (universal set), 通常记作 .
通常也把给定的集合作为全集.
定义 补集
对于一个集合 , 由全集 中不属于集合 的所有元素组成的集合称为集合 相对于全集 的补集 (complementary set),简称为集合 的补集, 记作 , 即
可用 Venn 图(图 1.3-4)表示.
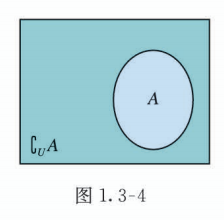
例 5
设 是小于 9 的正整数 , 求 , .
解:
根据题意可知, , 所以
例 6
设全集 是三角形 是锐角三角形 是钝角三角形 , 求 .
解:
根据三角形的分类可知
练习
1.
已知 , 求 .
2.
设 是平行四边形或梯形 是平行四边形 是菱形 是矩形 , 求 .
3.
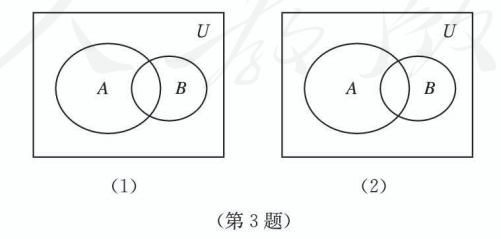
图中 是全集, 是 的两个子集, 用阴影表示:
(1) ;
(2) .
习题 1.3
复习巩固
1.
集合 , 求 .
2.
设 是小于 9 的正整数 . 求 , , .
3.
学校开运动会, 设 是参加 跑的同学 是参加 跑的同学 , 是参加 跑的同学 , 学校规定, 每个参加上述比赛的同学最多只能参加两项比赛, 请你用集合的运算说明这项规定, 并解释以下集合运算的含义:
(1) ;
(2) .
综合运用
4.
已知集合 , 求 , .
5.
设集合 , 求 .
拓广探索
6.
已知全集 , 试求集合 .