8.4 空间点、直线、平面之间的位置关系
2024-07-10 21:57:05 新建
前面我们初步认识了简单几何体的组成元素, 知道了顶点、棱 (直线段)、平面多边形是构成棱柱、棱锥等多面体的基本元素. 我们以直观感知的方式认识了这些基本元素之间的相互关系, 从而得到了多面体的一些结构特征. 为了进一步认识立体图形的结构特征,需要对点、直线、平面之间的位置关系进行研究. 本节我们先研究平面及其基本性质,在此基础上, 研究空间点、直线、平面之间的位置关系.
8.4.1 平面
定义 平面
在初中, 我们已经对点和直线有了一定的认识, 知道它们都是由现实事物抽象得到的. 生活中也有一些物体给我们以平面的直观感觉, 如课桌面、黑板面、平静的水面等.几何里所说的 “平面 (plane)” 就是从这样的一些物体中抽象出来的. 类似于直线向两端无限延伸, 平面是向四周无限延展的.
与画出直线的一部分来表示直线一样, 我们也可以画出平面的一部分来表示平面. 我们常用矩形的直观图, 即平行四边形表示平面. 如图 8.4-1, 当平面水平放置时, 常把平行四边形的一边画成横向; 当平面坚直放置时, 常把平行四边形的一边画成坚向.
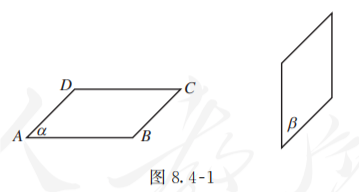
我们常用希腊字母 等表示平面, 如平面 、平面 、平面 等, 并将它写在代表平面的平行四边形的一个角内; 也可以用代表平面的平行四边形的四个顶点, 或者相对的两个顶点的大写英文字母作为这个平面的名称. 如图 8.4-1 中的平面 , 也可以表示为平面 、平面 或者平面 .
下面, 我们来研究平面的基本性质.
思考
我们知道, 两点可以确定一条直线, 那么几点可以确定一个平面?
在日常生活中, 我们常常可以看到这样的现象: 自行车用一个脚架和两个车轮着地就可以 “站稳”, 三脚架的三脚着地就可以支撑照相机 (图 8.4-2). 由这些事实和类似经验, 可以得到下面的基本事实:

基本事实 1
过不在一条直线上的三个点, 有且只有一个平面 (图 8.4-3).
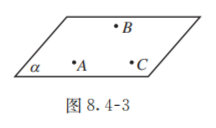
基本事实 1 给出了确定一个平面的依据. 它也可以简单说成 “不共线的三点确定一个平面”. 不在一条直线上的三个点 , 所确定的平面, 可以记成平面 .
定义
直线上有无数个点, 平面内有无数个点, 直线、平面都可以看作点的集合. 点 在直线 上, 记作 ; 点 在直线 外, 记作 ; 点 在平面 内, 记作 ; 点 在平面 外, 记作 .
思考
如果直线 与平面 有一个公共点 , 直线 是否在平面 内? 如果直线 与平面 有两个公共点呢?
在实际生活中, 我们有这样的经验: 如果一根直尺边缘上的任意两点在桌面上, 那么直尺的整个边缘就落在了桌面上. 上述经验和类似的事实可以归纳为以下基本事实:
基本事实 2
如果一条直线上的两个点在一个平面内, 那么这条直线在这个平面内(图 8.4-4).
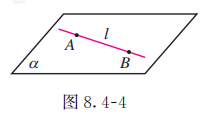
利用基本事实 2 , 可以判断直线是否在平面内.
定义
平面内有无数条直线, 平面可以看作直线的集合. 如果直线 上所有点都在平面 内, 就说直线 在平面 内, 记作 ; 否则, 就说直线 不在平面 内, 记作 .
基本事实 2 也可以用符号表示为
基本事实 2 表明,可以用直线的 “直” 刻画平面的 “平”,用直线的 “无限延伸” 刻画平面的 “无限延展”. 如图 8.4-5, 由基本事实 1 , 给定不共线三点 , 它们可以确定一个平面 ; 连接 , 由基本事实 2 , 这三条直线都在平面 内, 进而连接这三条直线上任意两点所得直线也都在平面 内,所有这些直线可以编织成一个 “直线网”, 这个 “直线网” 可以铺满平面 . 组成这个 “直线网” 的直线的 “直” 和向各个方向无限延伸, 说明了平面的 “平” 和 “无限延展”.
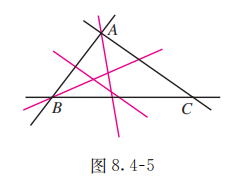
利用信息技术工具,可以方便地作出这个图形, 观察 “直线网” 的形成和编织成平面的过程,想象直线和平面的关系.
思考
如图 8.4-6, 把三角尺的一个角立在课桌面上,三角尺所在平面与课桌面所在平面是否只相交于一点 ? 为什么?
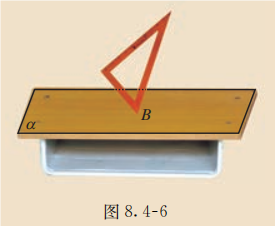
想象三角尺所在的无限延展的平面, 用它去 “穿透” 课桌面. 可以想象, 两个平面相交于一条直线. 教室里相邻的墙面在地面的墙角处有一个公共点, 这两个墙面相交于过这个点的一条直线. 由此我们又得到一个基本事实:
基本事实 3
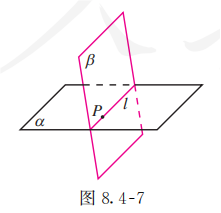
如果两个不重合的平面有一个公共点, 那么它们有且只有一条过该点的公共直线(图 8.4-7).
如无特殊说明, 本章中的两个平面均指两个不重合的平面.
基本事实 3 告诉我们, 如果两个平面有一个公共点, 那么这两个平面一定相交于过这个公共点的一条直线. 两个平面相交成一条直线的事实, 使我们进一步认识了平面的 “平”和 “无限延展”.
平面 与 相交于直线 , 记作 . 基本事实 3 可以用符号表示为
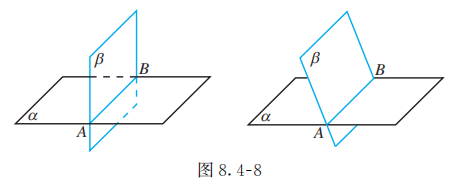
在画两个相交平面时, 如果其中一个平面的一部分被另一个平面挡住, 通常把被挡住的部分画成虚线或不画, 这样可使画出的图形立体感更强一些 (图 8.4-8).
上述三个关于平面的基本事实是人们经过长期观察与实践总结出来的, 是几何推理的基本依据, 也是我们进一步研究立体图形的基础.
推论
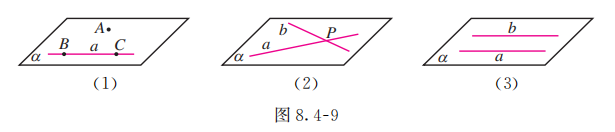
利用基本事实 1 和基本事实 2 , 再结合 “两点确定一条直线”, 可以得到下面三个推论 (图 8.4-9):
推论 1 经过一条直线和这条直线外一点, 有且只有一个平面.
推论 2 经过两条相交直线, 有且只有一个平面.
推论 3 经过两条平行直线, 有且只有一个平面.
证明
事实上, 如图 8.4-9 (1), 设点 是直线 外一点, 在直线 上任取两点 和 , 则由基本事实 1 , 经过 , 三点确定一个平面 . 再由基本事实 2 , 直线 也在平面 内, 因此平面 经过直线 和点 , 即一条直线和这条直线外一点确定一个平面.
思考
用类似的方法,你能说明推论 2 和推论 3 成立吗?
推论 1~3 给我们提供了确定一个平面的另外几种方法.
例子
如图 8.4-10, 用两根细绳沿桌子四条腿的对角拉直, 如果这两根细绳相交, 说明桌子四条腿的底端在同一个平面内,否则就不在同一个平面内,其依据就是推论 2.
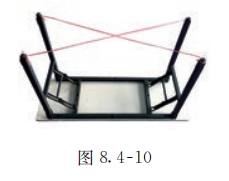
不共线的三点, 一条直线和这条直线外一点, 两条相交直线, 两条平行直线, 都能唯一确定一个平面. 这些结论在后续研究直线和平面之间平行、垂直关系时, 也会经常用到.
练习
1.
判断下列命题是否正确, 正确的在括号内画 “ ”, 错误的画 “ ”.
(1) 书桌面是平面.
(2) 平面 与平面 相交, 它们只有有限个公共点.
(3) 如果两个平面有三个不共线的公共点, 那么这两个平面重合.
2.
下列命题正确的是 .
(A) 三点确定一个平面
(B) 一条直线和一个点确定一个平面
(C) 圆心和圆上两点可确定一个平面
(D) 梯形可确定一个平面
3.
不共面的四点可以确定几个平面? 请画出图形说明你的结论.
4.
用符号表示下列语句, 并画出相应的图形:
(1) 点 在平面 内, 点 在平面 外;
(2) 直线 既在平面 内, 又在平面 内.
8.4.2 空间点、 直线、平面之间的位置关系
前面我们认识了空间中点、直线、平面之间的一些位置关系, 如点在平面内, 直线在平面内, 两个平面相交, 等等. 空间中点、直线、平面之间还有其他位置关系吗?
长方体是我们熟悉的空间几何图形, 下面我们借助长方体进一步研究空间中点、直线、平面之间的位置关系.
观察
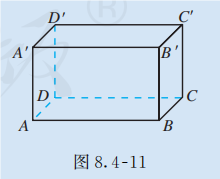
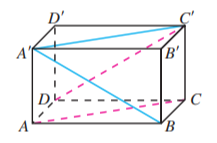
我们知道, 长方体有 8 个顶点, 12 条棱, 6 个面. 12 条棱对应 12 条棱所在的直线, 6 个面对应 6 个面所在的平面.观察如图 8.4-11 所示的长方体 , 你能发现这些顶点、直线、平面之间的位置关系吗?
观察你所在的教室, 你能找到上述位置关系的一些实例吗? 你能再举出一些表示这些位置关系的其他实例吗?
答
空间中点与直线的位置关系有两种: 点在直线上和点在直线外. 如图 8.4-11 中, 点 在直线 上, 在直线 外. 空间中点与平面的位置关系也有两种: 点在平面内和点在平面外. 如图 8.4-11 中, 点 在平面 内, 在平面 外.
下面我们研究空间中直线、平面之间的位置关系.
1. 空间中直线与直线的位置关系
在图 8.4-11 中, 直线 与 在同一个平面 内, 它们没有公共点, 它们是平行直线; 直线 与 也在同一个平面 内, 它们只有一个公共点 , 它们是相交直线;直线 与 不同在任何一个平面内.
定义
我们把不同在任何一个平面内的两条直线叫做异面直线. 于是, 空间两条直线的位置关系有三种:
这样, 空间中两条直线平行和我们学过的平面上两条直线平行的意义是一致的, 即首先这两条直线在同一平面内, 其次是它们不相交. 如果直线 为异面直线, 为了表示它们不共面的特点, 作图时, 通常用一个或两个平面衬托, 如图 8.4-12 所示.
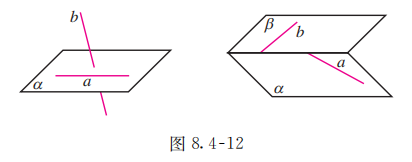
2. 空间中直线与平面的位置关系
在图 8.4-11 中, 直线 与平面 有无数个公共点; 直线 与平面 只有一个公共点 ; 直线 与平面 没有公共点. 再结合生活实例,
定理
我们可以看出, 直线与平面的位置关系有且只有三种:
(1) 直线在平面内 —— 有无数个公共点;
(2) 直线与平面相交 —— 有且只有一个公共点;
(3) 直线与平面平行 —— 没有公共点.
当直线与平面相交或平行时, 直线不在平面内, 也称为直线在平面外.
图 8.4-13 表示了直线与平面的三种位置关系.
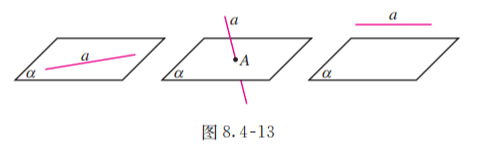
一般地, 直线 在平面 内, 应把直线 画在表示平面 的平行四边形内; 直线 在平面 外,应把直线 或它的一部分画在表示平面 的平行四边形外.
直线 与平面 相交于点 , 记作 ; 直线 与平面 平行, 记作 .
3. 空间中平面与平面的位置关系
在图 8.4-11 中, 平面 与平面 没有公共点; 平面 与平面 有一条公共直线 . 再结合生活实例,
定理
我们可以看出, 两个平面之间的位置关系有且只有以下两种:
(1) 两个平面平行 —— 没有公共点;
(2) 两个平面相交 —— 有一条公共直线.
画两个互相平行的平面时, 要注意使表示平面的两个平行四边形的对应边平行 (图 8.4-14).
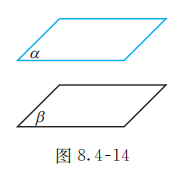
平面 与平面 平行, 记作 .
探究
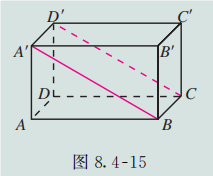
如图 8.4-15, 在长方体 中, 连接 , , 请你再举出一些图中表示空间直线、平面之间位置关系的例子, 并用符号表示这些位置关系.
与其他同学交流一下你的结果.
例 1
如图 8.4-16, 用符号表示下列图形中直线、平面之间的位置关系.
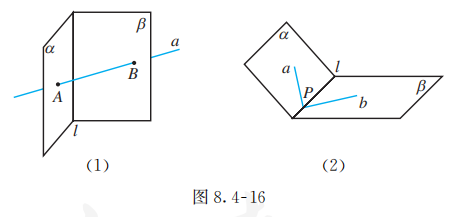
分析:
根据图形, 先判断直线、平面之间的位置关系, 然后用符号表示出来.
解:
在 (1) 中, .
在 (2) 中, .
例 2
如图 8.4-17, . 直线 与 具有怎样的位置关系? 为什么?
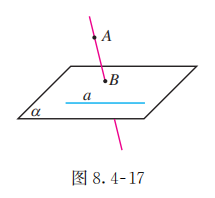
解:
直线 与 是异面直线. 理由如下.
若直线 与直线 不是异面直线, 则它们相交或平行. 设它们确定的平面为 , 则 . 由于经过点 与直线 有且仅有一个平面 , 因此平面 与 重合, 从而 , 进而 , 这与 矛盾. 所以直线 与 是异面直线.
定理
例 2 告诉我们一种判断异面直线的方法: 与一个平面相交的直线和这个平面内不经过交点的直线是异面直线.
练习
1.
选择题
(1) 如果两条直线 与 没有公共点,那么 与 .
(A) 共面
(B) 平行
(C) 是异面直线
(D) 可能平行,也可能是异面直线
(2) 设直线 分别是长方体的相邻两个面的对角线所在的直线, 则 与 .
(A) 平行
(B) 相交
(C) 是异面直线
(D) 可能相交,也可能是异面直线
2.
如图, 在长方体 中, 判定直线 与 , 直线 与 , 直线 与 , 直线 与 的位置关系.
3.
判断下列命题是否正确, 正确的在括号内画 “ ”, 错误的画 “ ”.
(1) 若直线 上有无数个点不在平面 内,则 .
(2) 若直线 与平面 平行,则 与平面 内的任意一条直线都平行.
(3) 如果两条平行直线中的一条与一个平面平行, 那么另一条也与这个平面平行.
(4) 若直线 与平面 平行,则 与平面 内的任意一条直线都没有公共点.
4.
已知直线 , 平面 , 且 . 判断直线 的位置关系, 并说明理由.
习题 8.4
复习巩固
1.
画出满足下列条件的图形:
(1) ;
(2) .
2.
选择题
(1) 经过同一直线上的 3 个点的平面 .
(A) 有且仅有 1 个
(B) 有且仅有 3 个
(C) 有无数个
(D) 不存在
(2) 若直线 不平行于平面 ,且 , 则下列结论成立的是 .
(A) 内的所有直线与 是异面直线
(B) 内不存在与 平行的直线
(C) 内存在唯一一条直线与 平行
(D) 内的所有直线与 都相交
3.
判断下列命题是否正确, 正确的在括号内画 “ ”, 错误的画 “ ”.
(1) 两两相交且不共点的三条直线确定一个平面.
(2) 四边形可以确定一个平面.
(3) 若 是两条直线, 是两个平面, 且 , 则 是异面直线.
4.
填空题
(1) 如果 是异面直线, 直线 与 都相交, 那么这三条直线中的两条所确定的平面共有 个;
(2) 若一条直线与两个平行平面中的一个平面平行, 则这条直线与另一个平面的位置关系是 ;
(3) 已知两条相交直线 , 且 平面 , 则 与 的位置关系是 .
5.
正方体各面所在平面将空间分成几部分?
综合运用
6.
如果一条直线与两条平行直线都相交, 那么这三条直线共面吗? 请说说你的理由.
7.
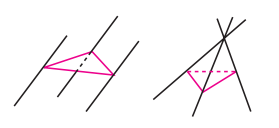
如图, 三条直线两两平行且不共面, 每两条直线确定一个平面, 一共可以确定几个平面? 如果三条直线相交于一点, 它们最多可以确定几个平面?
8.
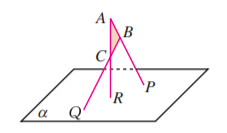
如图, 在平面 外, , 求证: 三点共线.
拓广探索
9.
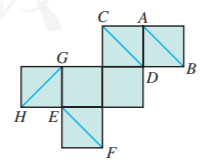
如图是一个正方体的展开图, 如果将它还原为正方体, 那么在 , 这四条线段中, 哪些线段所在直线是异面直线?
10.
在本节, 我们学习了平面, 了解了它的基本特征以及一些利用点、直线、平面等组成立体图形的基本元素刻画这些特征的方法. 类似地, 直线有什么基本特征? 如何刻画直线的这些基本特征?