4.7 数学建模
2024-03-05 22:19:35 新建
建立函数模型解决实际问题
我们知道, 用函数构建数学模型解决实际问题时, 首先要对实际问题中的变化过程进行分析, 析出其中的常量、变量及其相互关系; 明确其运动变化的基本特征, 从而确定它的运动变化类型. 然后根据分析结果, 选择适当的函数类型构建数学模型, 将实际问题化归为数学问题; 再通过运算、推理, 求解函数模型. 最后利用函数模型的解说明实际问题的变化规律, 达到解决问题的目的. 在构建函数模型时, 经常会遇到没有现成数据可用的情况, 这时就需要先收集数据.
数学建模活动的一个实例
1. 观察实际情景, 发现和提出问题
中国茶文化博大精深. 茶水的口感与茶叶类型和水的温度有关. 经验表明, 某种绿茶用 的水泡制, 再等到茶水温度降至 时饮用, 可以产生最佳口感. 那么在 室温下,刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感?
显然, 如果能建立茶水温度随时间变化的函数模型, 那么就能容易地解决这个问题.为此, 需要收集一些茶水温度随时间变化的数据, 再利用这些数据建立适当的函数模型.
2. 收集数据
我们可以利用秒表、温度计等工具 (若用计算机、数据采集器、温度传感器等信息技术更好),收集茶水温度随时间变化的数据.
例如, 某研究人员每隔 测量一次茶水温度, 得到表 1 的一组数据.

3. 分析数据
茶水温度是时间的函数, 但没有现成的函数模型. 为此, 可以先画出散点图, 利用图象直观分析这组数据的变化规律, 从而帮助我们选择函数类型.
设茶水温度从 开始, 经过 后的温度为 . 根据表 1 , 画散点图 (图 1).
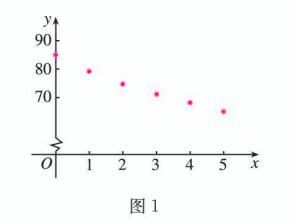
观察散点图的分布状况, 并考虑到茶水温度降至室温就不能再降的事实, 可选择函数 来近似地刻画茶水温度随时间变化的规律.
实际上, 你可以利用信息技术,通过函数拟合的方法来帮助选择适当的函数模型.
4. 建立模型
根据实际情况可知, 当 时, , 可得 .
为了求出温度的衰减比例 , 可从第 的温度数据开始, 计算每分 的值与上一分 值的比值, 列出表 2 .
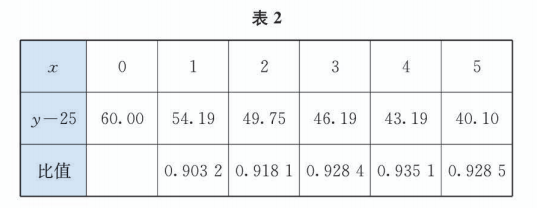
计算各比值的平均值, 得
我们把这个平均值作为衰减比例, 就得到一个函数模型
思考
能否直接将表 1 中的一组数据代入 求 ? 这与用比值的平均值作为 建立函数模型有什么差异?
5. 检验模型
将已知数据代人 (1) 式, 或画出函数 (1) 的图象 (图 2), 可以发现, 这个函数模型与实际数据基本吻合, 这说明它能较好地反映茶水温度随时间的变化规律.
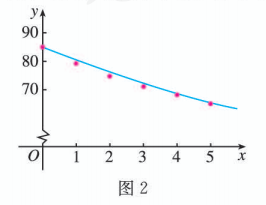
6. 求解问题
将 代人 , 得
解得
由信息技术得
所以, 泡制一杯最佳口感茶水所需时间大约是 .
上述过程可以概括为:
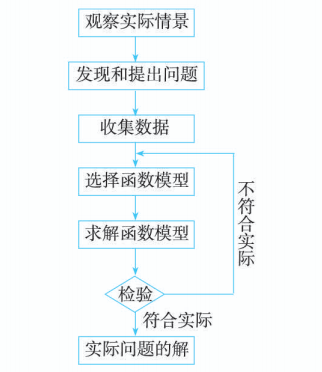
数学建模活动的选题
探究
请同学们仿照上述过程开展一次建立函数模型解决实际问题的活动. 可以继续研究不同室温下泡制一杯最佳口感茶水所需的时间, 也可以从下列选题中选择一个:
- 应在炒菜之前多长时间将冰箱里的肉拿出来解冻?
- 根据某一同学的身高和体重, 判断该同学是否超重.
- 用微波炉或电磁炉烧一壶开水, 找到最省电的功率设定方法.
- 估计阅读一本书所需要的时间.
也可以根据自己的兴趣, 与老师协商后确定一个课题进行研究.
数学建模活动的要求
1. 组建合作团队
数学建模活动需要团队协作. 首先, 在班级中组成 人的研究小组, 每位同学参加其中一个小组. 在小组内, 要确定一个课题负责人, 使每位成员都有明确的分工. 拟定研究课题、确定研究方案、规划研究步骤、编制研究手册, 然后在班里进行一次开题报告.
2. 开展研究活动
根据开题报告所规划的研究步骤, 通过背景分析、数据收集、数据分析、数学建模、获得结论等过程, 完成课题研究. 在研究过程中, 可以借助信息技术解决问题.
3. 撰写研究报告
以小组为单位, 撰写一份研究报告.
4. 交流展示
(1) 对同一个课题, 先由 个小组进行小组交流, 每个小组都展示自己的研究成果, 相互借鉴、取长补短. 在小组研究报告的基础上形成大组的研究报告. 选定代表, 制作向全班汇报的演示文稿.
(2) 与老师一起进行全班研究成果展示与交流, 在各组代表作研究报告的基础上, 通过质疑、辩论、评价, 总结成果, 分享体会, 分析不足. 开展自我评价、同学评价和老师评价, 完成本次数学建模活动.
数学建模活动研究报告的参考形式
建立函数模型解决实际问题
_ _ _ 年 _ _ _ 班
完成时间: _ _ _
- 课题名称
- 课题组成员及分工
- 选题的意义
- 研究计划 (包括对选题的分析, 解决问题的思路等)
- 研究过程 (收集数据、分析数据、建立模型、求解模型的过程, 以及过程中出现的难点及解决方案等)
- 研究结果
- 收获与体会
- 对此研究的评价 (由评价小组或老师填写)