3.4 函数的应用 (一)

2024-02-06 22:09:03 新建

我们学习过的一次函数、二次函数、幂函数等都与现实世界有紧密联系. 下面通过一些实例感受它们的广泛应用,体会利用函数模型解决实际问题的过程与方法.

例 1

设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与 3.1.2 例 8 相同, 全年综合所得收入额为 $x$ (单位: 元), 应缴纳综合所得个税税额为 $y$ (单位: 元).
(1) 求 $y$ 关于 $x$ 的函数解析式;
(2) 如果小王全年的综合所得由 117600 元增加到 153600 元, 那么他全年应缴纳多少综合所得个税?

分析:

根据 3.1.2 例 8 中公式 ② , 可得应纳税所得额 $t$ 关于综合所得收入额 $x$ 的解析式 $t = g (x)$ , 再结合 $y = f (t)$ 的解析式 ③ , 即可得出 $y$ 关于 $x$ 的函数解析式.

解：

(1) 由个人应纳税所得额计算公式, 可得

$t = x - 60000 - x (8 % + 2 % + 1 % + 9 %) - 9600 - 560 = 0.8 x - 70160 .$

令 $t = 0$ , 得 $x = 87700$ .

根据个人应纳税所得额的规定可知, 当 $0 ⩽ x ⩽ 87700$ 时, $t = 0$ . 所以, 个人应纳税所得额 $t$ 关于综合所得收人额 $x$ 的函数解析式为

$t = {0, 0 ⩽ x ⩽ 87700, 0.8 x - 70160, x > 87700 .$

结合 3.1.2 例 8 的解析式 ③ , 可得:
当 $0 ⩽ x ⩽ 87700$ 时, $t = 0$ , 所以 $y = 0$ ；
当 $87700 < x ⩽ 132700$ 时, $0 < t ⩽ 36000$ , 所以

$y = t \times 3 % = 0.024 x - 2104.8;$

当 $132700 < x ⩽ 267700$ 时, $36000 < t ⩽ 144000$ , 所以

$y = t \times 10 % - 2520 = 0.08 x - 9536;$

当 $267700 < x ⩽ 462700$ 时, $144000 < t ⩽ 300000$ , 所以

$y = t \times 20 % - 16920 = 0.16 x - 30952;$

当 $462700 < x ⩽ 612700$ 时, $300000 < t ⩽ 420000$ , 所以

$y = t \times 25 % - 31920 = 0.2 x - 49460;$

当 $612700 < x ⩽ 912700$ 时, $420000 < t ⩽ 660000$ , 所以

$y = t \times 30 % - 52920 = 0.24 x - 73968;$

当 $912700 < x ⩽ 1287700$ 时, $660000 < t ⩽ 960000$ , 所以

$y = t \times 35 % - 85920 = 0.28 x - 110476;$

当 $x > 1287700$ 时, $t > 960000$ , 所以

$y = t \times 45 % - 181920 = 0.36 x - 213492 .$

所以, 函数解析式为

$y = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 0, 0 ⩽ x ⩽ 87700, 0.024 x - 2104.8, 87700 < x ⩽ 132700, 0.08 x - 9536, 132700 < x ⩽ 267700, 0.16 x - 30952, 267700 < x ⩽ 462700, 0.2 x - 49460, 462700 < x ⩽ 612700, 0.24 x - 73968, 612700 < x ⩽ 912700, 0.28 x - 110476, 912700 < x ⩽ 1287700, 0.36 x - 213492, x > 1287700 . (④)$

(2) 根据 ④ , 当 $x = 153600$ 时,

$y = 0.08 \times 153600 - 9536 = 2752 .$

所以, 小王全年需要缴纳的综合所得个税税额为 2752 元.

根据个人收人情况, 利用上面获得的个税和综合所得收人关系的函数解析式, 就可以直接求得应缴纳的个税.

例 2

一辆汽车在某段路程中行驶的平均速率 $v$ (单位: $k m / h$ ) 与时间 $t$ (单位: h) 的关系如图 3.4-1 所示,
(1) 求图 3.4-1 中阴影部分的面积, 并说明所求面积的实际含义;
(2) 假设这辆汽车的里程表在汽车行驶这段路程前的读数为 $2004 k m$ , 试建立行驶这段路程时汽车里程表读数 $s$ (单位: $k m$ )与时间 $t$ 的函数解析式, 并画出相应的图象.

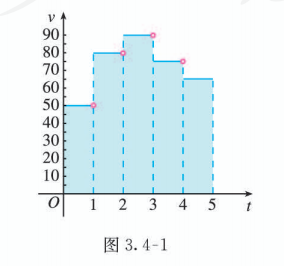
你能根据图 3.4-1 画出汽车行驶路程关于时间变化的图象吗?

分析：

当时间 $t$ 在 $[0, 5]$ 内变化时, 对于任意的时刻 $t$ 都有唯一确定的行驶路程与之相对应. 根据图 3.4-1, 在时间段 $[0, 1), [1, 2), [2, 3), [3, 4), [4, 5]$ 内行驶的平均速率分别为 $50 k m / h, 80 k m / h, 90 k m / h, 75 k m / h, 65 k m / h$ , 因此在每个时间段内，行驶路程与时间的关系也不一样，需要分段表述.

解：

(1) 阴影部分的面积为

$50 \times 1 + 80 \times 1 + 90 \times 1 + 75 \times 1 + 65 \times 1 = 360 .$

阴影部分的面积表示汽车在这 $5 h$ 内行驶的路程为 $360 k m$ .
(2) 根据图 3.4-1, 有

$s = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 50 t + 2004, 0 ⩽ t < 1, 80 (t - 1) + 2054, 1 ⩽ t < 2, 90 (t - 2) + 2134, 2 ⩽ t < 3, 75 (t - 3) + 2224, 3 ⩽ t < 4, 65 (t - 4) + 2299, 4 ⩽ t ⩽ 5 .$

这个函数的图象如图 3.4-2 所示.

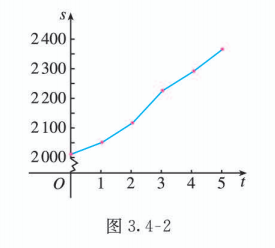
本题的解答过程表明, 函数图象对分析和理解题意很有帮助. 因此, 我们要注意提高读图能力. 另外, 本题用到了分段函数, 解决现实问题时经常会用到这类函数.

练习

若用模型 $y = a x^{2}$ 描述汽车紧急刹车后滑行的距离 $y$ (单位: $m$ ) 与刹车时的速率 $x$ (单位: $k m / h$ )的关系,而某种型号的汽车在速率为 $60 k m / h$ 时, 紧急刹车后滑行的距离为 $20 m$ . 在限速为 $100 k m / h$ 的高速公路上, 一辆这种型号的车紧急刹车后滑行的距离为 $50 m$ , 那么这辆车是否超速行驶?

某广告公司要为客户设计一幅周长为 $l$ (单位: $m$ ) 的矩形广告牌, 如何设计这个广告牌可以使广告牌的面积最大?

某公司生产某种产品的固定成本为 150 万元, 而每件产品的可变成本为 2500 元, 每件产品的售价为 3500 元. 若该公司所生产的产品全部销售出去, 则
(1) 设总成本为 $y_{1}$ (单位: 万元), 单位成本为 $y_{2}$ (单位: 万元), 销售总收人为 $y_{3}$ (单位: 万元),总利润为 $y_{4}$ (单位: 万元), 分别求出它们关于总产量 $x$ (单位: 件)的函数解析式;
(2) 根据所求函数的图象, 对这个公司的经济效益做出简单分析.

习题 3.4

综合运用

某人开汽车以 $60 k m / h$ 的速率从 $A$ 地到 $150 k m$ 远处的 B地, 在 B 地停留 $1 h$ 后, 再以 $50 k m / h$ 的速率返回 $A$ 地. 把汽车与 $A$ 地的距离 $x$ (单位: $k m$ ) 表示为时间 $t$ (单位: $h$ ) (从 $A$ 地出发时开始) 的函数; 再把车速 $v$ (单位: $k m / h$ ) 表示为时间 $t$ 的函数, 并分别画出这两个函数的图象.

要建造一个容积为 $1200 m^{3}$ , 深为 $6 m$ 的长方体无盖蓄水池, 池壁的造价为 95 元 $/ m^{2}$ , 池底的造价为 135 元 $/ m^{2}$ , 如何设计水池的长与宽, 才能使水池的总造价控制在 7 万元以内（精确到 $0.1 m$ )?

为了保护水资源，提倡节约用水，某城市对居民生活用水实行 “阶梯水价”. 计费方法如下表：

每户每月用水量	水价
不超过 $12 m^{3}$ 的部分	3 元 $/ m^{3}$
超过 $12 m^{3}$ 但不超过 $18 m^{3}$ 的部分	6 元 $/ m^{3}$
超过 $18 m^{3}$ 的部分	9 元 $/ m^{3}$

若某户居民本月交纳的水费为 48 元, 求此户居民本月用水量.

拓广探索

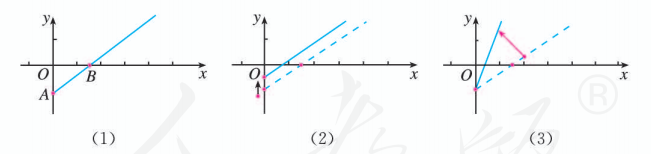
图 (1) 是某条公共汽车线路收支差额 $y$ 关于乘客量 $x$ 的图象.
(1) 试说明图 (1) 上点 $A$ , 点 $B$ 以及射线 $A B$ 上的点的实际意义;
(2) 由于目前本条线路亏损，公司有关人员提出了两种扭亏为赢的建议，如图 (2) (3) 所示.你能根据图象, 说明这两种建议是什么吗?

下表是拉力 $F$ (单位: $N$ )与弹簧伸长长度 $x$ (单位: $c m$ )的相关数据:

$F$	1	2	3	4	5
$x$	14.2	28.8	41.3	57.5	70.2

描点画出弹簧伸长长度随拉力变化的图象, 并写出一个能基本反映这一变化现象的函数解析式.