3.3 幂函数

2024-02-05 22:26:20 新建

前面学习了函数的概念, 利用函数概念和对图象的观察, 研究了函数的一些性质. 本节我们利用这些知识研究一类新的函数. 先看几个实例.

例子

(1) 如果张红以 1 元 $/ k g$ 的价格购买了某种蔬菜 $w k g$ ,那么她需要支付 $p = w$ 元，这里 $p$ 是 $w$ 的函数;
(2) 如果正方形的边长为 $a$ , 那么正方形的面积 $S = a^{2}$ ,这里 $S$ 是 $a$ 的函数;
(3) 如果立方体的棱长为 $b$ , 那么立方体的体积 $V = b^{3}$ ,这里 $V$ 是 $b$ 的函数;
(4) 如果一个正方形场地的面积为 $S$ , 那么这个正方形的边长 $c = S$ , 这里 $c$ 是 $S$ 的函数;
( $S$ 也可以表示为 $S^{\frac{1}{2}}$ .)
(5) 如果某人 $t s$ 内骑车行进了 $1 k m$ , 那么他骑车的平均速度 $v = \frac{1}{t} k m / s$ , 即 $v = t^{- 1}$ , 这里 $v$ 是 $t$ 的函数.

观察

观察（1）~（5）中的函数解析式, 它们有什么共同特征?

观察结果

实际上, 这些函数的解析式都具有幂的形式, 而且都是以幂的底数为自变量; 幕的指数都是常数, 分别是 $1, 2, 3, \frac{1}{2}, - 1$ ; 它们都是形如 $y = x^{α}$ 的函数.

定义幂函数

一般地, 函数 $y = x^{α}$ 叫做幂函数（power function), 其中 $x$ 是自变量, $α$ 是常数.

幕的指数除了可以取整数之外, 还可以取其他实数, 当它们取其他实数时幂也具有各自的含义,这些会在后面学习.

对于幂函数, 我们只研究 $α = 1, 2, 3, \frac{1}{2}, - 1$ 时的图象与性质.

思考

结合以往学习函数的经验, 你认为应该如何研究这些函数?

过程

通常可以先根据函数解析式求出函数的定义域, 画出函数的图象; 再利用图象和解析式, 讨论函数的值域、单调性、奇偶性等问题.

在同一坐标系中画出函数 $y = x, y = x^{2}, y = x^{3}, y = x^{\frac{1}{2}}$ 和 $y = x^{- 1}$ 的图象 (图 3.3-1).

探究

观察函数图象并结合函数解析式, 将你发现的结论写在表 3.3-1 内.

这些函数图象有公共点吗?

结果

通过图 3.3-1 与表 3.3-1, 我们得到:
(1) 函数 $y = x, y = x^{2}, y = x^{3}, y = x^{\frac{1}{2}}$ 和 $y = x^{- 1}$ 的图象都通过点 $(1, 1)$ ;
(2) 函数 $y = x, y = x^{3}, y = x^{- 1}$ 是奇函数, 函数 $y = x^{2}$ 是偶函数;
(3) 在区间 $(0, + \infty)$ 上, 函数 $y = x, y = x^{2}, y = x^{3}, y = x^{\frac{1}{2}}$ 单调递增, 函数 $y = x^{- 1}$ 单调递减;
(4) 在第一象限内, 函数 $y = x^{- 1}$ 的图象向上与 $y$ 轴无限接近, 向右与 $x$ 轴无限接近.

例

证明幂函数 $f (x) = x$ 是增函数.

证明:

函数的定义域是 $[0, + \infty)$ .
$\forall x_{1}, x_{2} \in [0, + \infty)$ , 且 $x_{1} < x_{2}$ , 有

$f (x_{1}) - f (x_{2}) = x_{1} - x_{2} = \frac{( x _{1} - x _{2} ) ( x _{1} + x _{2} )}{x _{1} + x _{2}} = \frac{x _{1} - x _{2}}{x _{1} + x _{2}} .$

因为

$x_{1} - x_{2} < 0, x_{1} + x_{2} > 0,$

所以 $f (x_{1}) < f (x_{2})$ , 即幂函数 $f (x) = x$ 是增函数.

练习

已知幕函数 $y = f (x)$ 的图象过点 $(2, 2)$ , 求这个函数的解析式.

利用幂函数的性质, 比较下列各题中两个值的大小:
(1) $(- 1.5)^{3}, (- 1.4)^{3}$ ;
(2) $\frac{1}{- 1 . 5}, \frac{1}{- 1 . 4}$ .

根据单调性和奇偶性的定义, 讨论函数 $f (x) = x^{3}$ 的单调性, 并判断其奇偶性.

习题 3.3

复习巩固

画出函数 $y = ∣ x ∣$ 的图象, 并判断函数的奇偶性, 讨论函数的单调性.

综合运用

在固定压力差 (压力差为常数) 下, 当气体通过圆形管道时, 其流量 $v$ (单位: $c m^{3} / s$ ) 与管道半径 $r$ (单位: $c m$ ) 的四次方成正比.
(1) 写出气体流量 $v$ 关于管道半径 $r$ 的函数解析式;
(2) 若气体在半径为 $3 c m$ 的管道中, 流量为 $400 c m^{3} / s$ , 求该气体通过半径为 $r$ 的管道时, 其流量 $v$ 的表达式;
(3) 已知 (2) 中的气体通过的管道半径为 $5 c m$ , 计算该气体的流量（精确到 $1 c m^{3} / s$ ).

试用描点法画出函数 $f (x) = x^{- 2}$ 的图象, 求函数的定义域、值域; 讨论函数的单调性、奇偶性, 并证明.

探究与发现

探究函数 $y = x + \frac{1}{x}$ 的图象与性质

在初中, 我们知道 $y = x$ 是正比例函数, $y = \frac{1}{x}$ 是反比例函数. 学习了幂函数以后, 我们知道它们都是幕函数. 不同的函数通过加、减、乘、除等运算可以构成新的函数. 那么, 将这两个函数相加构成的函数有哪些性质? 这些性质与这两个函数的性质有联系吗?

下面请同学们带着问题探究一下函数 $y = x + \frac{1}{x}$ .

你认为可以从哪些方面研究这个函数?
你认为可以按照怎样的路径研究这个函数?
按照你构建的路径研究你想到的问题.
证明: 当 $x > 0$ 时, $x + \frac{1}{x} ⩾ 2$ , 当且仅当 $x = \frac{1}{x}$ , 即 $x = 1$ 时取得等号; 当 $x < 0$ 时, $x + \frac{1}{x} ⩽ - 2$ , 当且仅当 $x = \frac{1}{x}$ , 即 $x = - 1$ 时取得等号.
你画出的函数图象与图 1 类似吗?
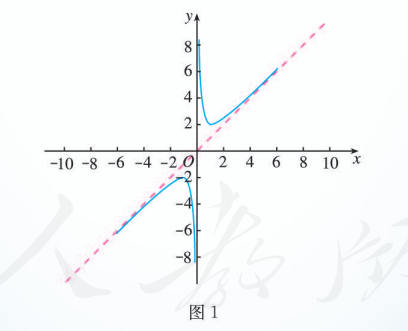
函数 $y = x + \frac{1}{x}$ 的图象有什么变化趋势? 你能利用函数 $y = x$ 和 $y = \frac{1}{x}$ 的图象变化趋势说明函数 $y = x + \frac{1}{x}$ 的图象变化趋势吗?
通过对函数 $y = x + \frac{1}{x}$ 图象与性质的探究, 你有哪些体会?