3.5 小结
2024-02-07 22:17:15 新建
探究 函数的形成与发展
了解函数形成、发展的历史.
- 函数产生的社会背景.
- 函数概念发展的历史过程.
- 函数符号的故事.
- 数学家与函数.
众多数学家对函数的完善作出了贡献, 例如开普勒、伽利略、笛卡儿、牛顿、莱布尼茨和欧拉等. 可以选取一位或多位数学家, 说明他们对函数发展作出的贡献, 感受数学家的精神.
本章知识结构
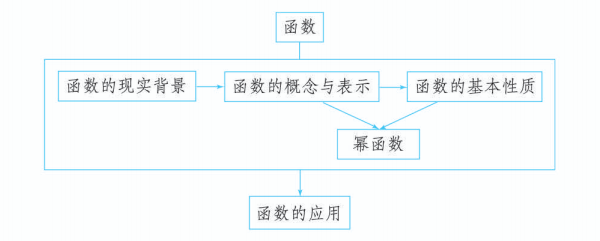
回顾与思考
本章我们用集合的语言与对应关系进一步描述了函数概念. 与初中的函数定义相比较, 突出了函数概念的本质: 两个数集之间的一种确定的对应关系; 明确了函数的三个构成要素: 定义域、对应关系和值域; 引入了函数符号: .与初中基于变量关系的函数定义相比, 本章基于两个实数集之间对应关系的函数定义, 抽象层次显然提高了. 在今后的学习中我们会逐渐体会到这种函数定义的必要性, 例如, 在这种定义下, 不同的函数可以进行加、减、乘、除等运算, 从而使函数研究的内容和应用的范围得到扩展.
函数是描述变量之间依赖关系的重要数学模型. 函数的表示方法主要有解析法、图象法、列表法等. 在解决问题时, 面对不同的需要, 选择恰当的方法表示函数是很重要的.
研究函数的基本性质不仅是解决实际问题的需要, 也是数学本身的自然要求. 例如: 事物的变化趋势, 用料最省、利润最大、效率最高, 对称性等, 这些特性反映在函数上, 就是函数的基本性质, 如单调性、最大(小)值和奇偶性等. 在研究这些基本性质时, 一般是先从几何直观 (观察图象) 入手, 然后运用自然语言描述函数的图象特征, 最后抽象到用数学符号刻画相应的数量特征. 研究某个函数的性质, 则要利用单调性、奇偶性等定义, 通过推理、运算来实现. 这是一个渐进的过程, 也是数学学习和研究中经常使用的方法.
本章的学习对后面研究有关函数问题具有指导作用, 我们可以按照下面的 “逻辑图” 获得研究内容:
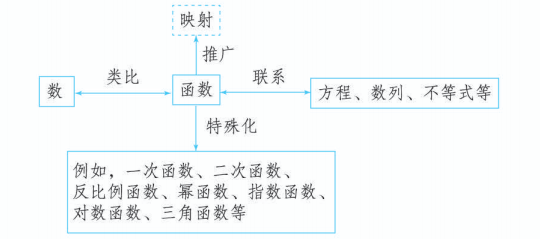
思考
请你带着下面的问题, 复习一下全章内容吧!
- 通过本章学习, 你对函数概念有什么新的认识?
- 你能结合具体实例, 分析、比较函数的各种表示方法的特点吗?
- 函数的性质一般包括哪些方面? 为什么要研究这些性质? 你能总结一下研究函数性质的一般过程和方法吗?
复习参考题 3
复习巩固
1.
求下列函数的定义域:
(1) ;
(2) .
2.
已知函数 , 求:
(1) ;
(2) .
3.
设 , 求证:
(1) ;
(2) .
4.
已知函数 在 上具有单调性, 求实数 的取值范围.
5.
已知幂函数 的图象过点 , 试求出此函数的解析式, 并画出图象, 判断奇偶性、单调性.
6.
某公司生产某种电子仪器的固定成本为 20000 元, 每生产一台仪器需增加投人 100 元, 已知总收入 (单位: 元) 关于月产量 (单位: 台) 满足函数:
(1) 将利润 (单位: 元) 表示为月产量 的函数;
(2) 当月产量为何值时, 公司所获利润最大? 最大利润为多少元? (总收入 总成本 利润)
综合运用
7.
已知函数 求 的值.
8.
证明:
(1) 若 , 则 ;
(2) 若 , 则 .
9.
(1) 已知奇函数 在 上单调递减, 那么它在 上单调递增还是单调递减?
(2) 已知偶函数 在 上单调递减, 那么它在 上单调递增还是单调递减?
10.
某地区上年度电价为 0.8 元 , 年用电量为 , 本年度计划将电价下降到 0.55 元 至 0.75 元 之间, 而用户期望电价为 0.4 元 . 经测算, 下调电价后新增用电量和实际电价与用户的期望电价的差成反比 (比例系数为 ). 该地区的电力成本价为 0.3 元 .
(1) 写出本年度电价下调后电力部门的收益 (单位: 元) 关于实际电价 (单位: 元 )的函数解析式; (收益 实际电量 (实际电价 成本价))
(2) 设 , 当电价最低定为多少时, 仍可保证电力部门的收益比上年至少增长 ?
拓广探索
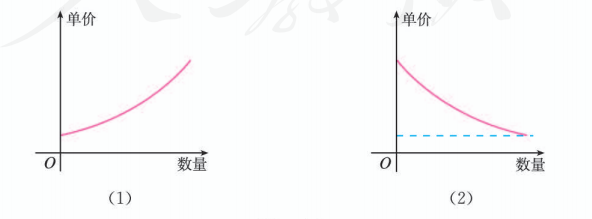
11.
经济学家在研究供求关系时, 一般用纵轴表示产品价格 (自变量), 而用横轴来表示产品数量 (因变量). 下列供求曲线, 哪条表示厂商希望的供应曲线, 哪条表示客户希望的需求曲线?为什么?
12.
试讨论函数 的定义域、值域、单调性、奇偶性, 并画出函数图象.
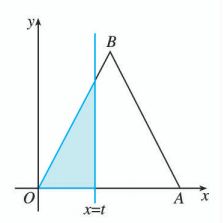
13.
如图, 是边长为 2 的正三角形, 记 位于直线 左侧的图形的面积为 . 试求函数 的解析式, 并画出函数 的图象.
14.
某商场经营一批进价为 30 元/件的商品, 在市场试销中发现, 此商品的销售单价 (单位: 元)与日销售量 (单位: 件)之间有如下表所示的关系.
| 30 | 40 | 45 | 50 | |||
|---|---|---|---|---|---|---|
| 60 | 30 | 15 | 0 |
(1) 根据表中提供的数据描出实数对 的对应点, 根据画出的点猜想 与 之间的函数关系, 并写出一个函数解析式;
(2) 设经营此商品的日销售利润为 (单位: 元), 根据上述关系,写出 关于 的函数解析式, 并求销售单价为多少元时, 才能获得最大日销售利润.