8.3 简单几何体的表面积与体积
2024-07-06 20:54:01 新建
前面我们分别认识了基本立体图形的结构特征和平面表示, 本节进一步认识简单几何体的表面积和体积. 表面积是几何体表面的面积, 它表示几何体表面的大小, 体积是几何体所占空间的大小.
8.3.1 棱柱、棱锥、棱台的表面积和体积
1. 棱柱、棱锥、棱台的表面积
定义
多面体的表面积就是围成多面体各个面的面积的和. 棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
例 1
如图 8.3-1, 四面体 的各棱长均为 , 求它的表面积.
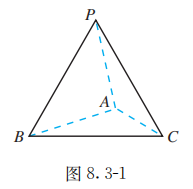
分析:
因为四面体 的四个面是全等的等边三角形, 所以四面体的表面积等于其中任何一个面的面积的 4 倍.
解:
因为 是正三角形, 其边长为 , 所以 .
因此, 四面体 的表面积
2. 棱柱、棱锥、棱台的体积
定理
我们以前已经学习了特殊的棱柱——正方体、长方体的体积公式, 它们分别是
( 是正方体的棱长),
( 分别是长方体的长、宽、高).
定理
一般地, 如果棱柱的底面积是 , 高是 , 那么这个棱柱的体积
定义
棱柱的高是指两底面之间的距离, 即从一底面上任意一点向另一个底面作垂线, 这点与垂足 (垂线与底面的交点) 之间的距离.
定理
如果一个棱柱和一个棱锥的底面积相等, 高也相等, 那么, 棱柱的体积是棱锥的体积的 3 倍. 因此, 一般地, 如果棱锥的底面面积为 , 高为 , 那么该棱锥的体积
定义
棱锥的高是指从顶点向底面作垂线, 顶点与垂足之间的距离.
定理
由于棱台是由棱锥截成的, 因此可以利用两个棱锥的体积差, 得到棱台的体积公式
其中 分别为棱台的上、下底面面积, 为棱台的高.
定义
棱台的高是指两底面之间的距离, 即从上底面上任意一点向下底面作垂线, 这点与重足之间的距离.
思考
观察棱柱、棱锥、棱台的体积公式
它们之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
例 2
如图 8.3-2, 一个漏斗的上面部分是一个长方体, 下面部分是一个四棱锥, 两部分的高都是 , 公共面 是边长为 的正方形, 那么这个漏斗的容积是多少立方米(精确到 )?(计算漏斗的容积时不考虑漏斗的厚度)

分析:
漏斗由两个多面体组成, 其容积就是两个多面体的体积和.
解:
由题意知
所以这个漏斗的容积
练习
1.
正六棱台的上、下底面边长分别是 和 , 侧棱长是 , 求它的表面积.
2.
如图是一个表面被涂上红色的棱长是 的立方体, 将其适当分割成棱长为 的小立方体.
(1) 共得到多少个棱长是 的小立方体?
(2) 三面是红色的小立方体有多少个? 它们的表面积之和是多少?
(3) 两面是红色的小立方体有多少个? 它们的表面积之和是多少?
(4) 一面是红色的小立方体有多少个? 它们的表面积之和是多少?
(5) 六个面均没有颜色的小立方体有多少个? 它们的表面积之和是多少? 它们占有多少立方厘米的空间?

3.
某广场设置了一些石凳供大家休息, 这些石凳是由正方体截去八个一样的四面体得到的. 如果被截正方体的棱长是 , 那么石凳的体积是多少?

4.
求证: 直三棱柱的任意两个侧面的面积和大于第三个侧面的面积.
8.3.2 圆柱、圆锥、圆台、球的表面积和体积
1. 圆柱、圆锥、圆台的表面积和体积
定理
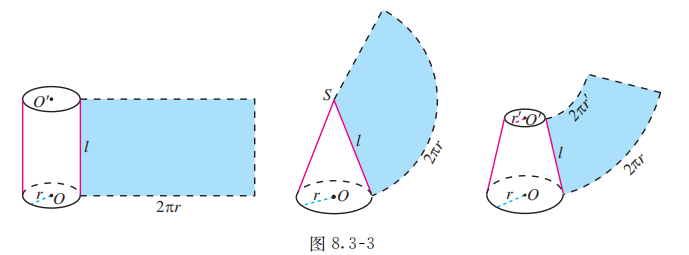
与多面体的表面积一样, 圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和. 利用圆柱、圆锥、圆台的展开图 (图 8.3-3), 可以得到它们的表面积公式:
( 是底面半径, 是母线长),
( 是底面半径, 是母线长),
分别是上、下底面半径, 是母线长).
思考
圆柱、圆锥、圆台的表面积公式之间有什么关系? 你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
定理
我们以前学习过圆柱、圆锥的体积公式, 即
由于圆台是由圆锥截成的, 因此可以利用圆锥的体积公式推导出圆台的体积公式
分别是上、下底面半径, 是高).
思考
圆柱、圆锥、圆台的体积公式之间有什么关系? 结合棱柱、棱锥、棱台的体积公式, 你能将它们统一成柱体、锥体、台体的体积公式吗? 柱体、锥体、台体的体积公式之间又有怎样的关系?
归纳
( 为底面积, 为柱体高);
( 为底面积, 为锥体高);
.
当 时,台体变为柱体,台体的体积公式也就是柱体的体积公式; 当 时, 台体变为锥体, 台体的体积公式也就是锥体的体积公式.
2. 球的表面积和体积
定理
设球的半径为 ,它的表面积只与半径 有关,是以 为自变量的函数.
事实上,如果球的半径为 ,那么它的表面积是
例 3
如图 8.3-4, 某种浮标由两个半球和一个圆柱黏合而成, 半球的直径是 ,圆柱高 . 如果在浮标表面涂一层防水漆,每平方米需要 涂料,那么给 1000 个这样的浮标涂防水漆需要多少涂料? ( 取 3.14)

解:
一个浮标的表面积为
所以给 1000 个这样的浮标涂防水漆约需涂料
思考
在小学, 我们学习了圆的面积公式, 你还记得是如何求得的吗? 类比这种方法, 你能由球的表面积公式推导出球的体积公式吗?
答
类比利用圆周长求圆面积的方法, 我们可以利用球的表面积求球的体积. 如图 8.3-5, 把球 的表面分成 个小网格,连接球心 和每个小网格的顶点, 整个球体就被分割成 个 “小锥体”.
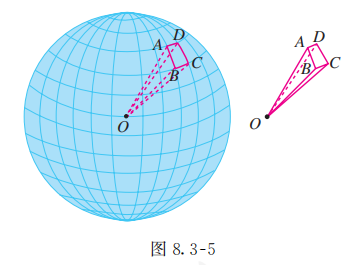
当 越大,每个小网格越小时,每个 “小锥体” 的底面就越平,“小锥体” 就越近似于棱锥,其高越近似于球半径 . 设 是其中一个 “小锥体”,它的体积
由于球的体积就是这 个 “小锥体” 的体积之和, 而这 个 “小锥体” 的底面积之和就是球的表面积. 因此, 球的体积
定理
由此, 我们得到球的体积公式
例 4
如图 8.3-6, 圆柱的底面直径和高都等于球的直径, 求球与圆柱的体积之比.
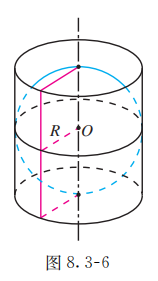
解:
设球的半径为 ,则圆柱的底面半径为 ,高为 .
,
.
本节我们学习了柱体、锥体、台体、球的表面积与体积的计算方法. 在生产、生活中遇到的物体, 往往形状比较复杂, 但很多物体都可以看作由这些简单几何体组合而成的, 它们的表面积与体积可以利用这些简单几何体的表面积与体积来计算.
练习
1.
已知圆锥的表面积为 , 且它的侧面展开图是一个半圆, 求这个圆锥的底面直径.
2.
当一个球的半径满足什么条件时, 其体积和表面积的数值相等?
3.
将一个棱长为 的正方体铁块磨制成一个球体零件, 求可能制作的最大零件的体积.
4.
一个长、宽、高分别是 的水槽中装有 的水, 现放入一个直径为 的木球. 如果木球的三分之二在水中, 三分之一在水上, 那么水是否会从水槽中溢出?
习题 8.3
复习巩固
1.
如图, 八面体的每一个面都是正三角形, 并且 4 个顶点 在同一个平面内. 如果四边形 是边长为 的正方形, 那么这个八面体的表面积是多少?
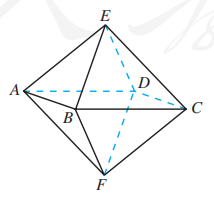
2.
如图,将一个长方体沿相邻三个面的对角线截出一个棱锥,求棱锥的体积与剩下的几何体体积的比.
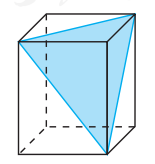
3.
如图, 一个直三棱柱形容器中盛有水, 侧棱 . 若侧面 水平放置时, 水面恰好过 的中点. 那么当底面 水平放置时, 水面高为多少?
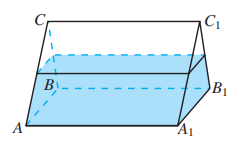
4.
如图, 圆锥 的底面直径和高均是 , 过 的中点 作平行于底面的截面, 以该截面为底面挖去一个圆柱, 求剩下几何体的表面积和体积.

5.
一个正方体的顶点都在球面上, 它的棱长是 , 求球的体积.
综合运用
6.
如图是一个烟筒的直观图(图中数据的单位为厘米), 它的下部是一个正四棱台形物体, 上部是一个正四棱柱形物体 (底面与四棱台形物体的上底面重合). 为防止雨水的侵蚀, 同时使烟筒更美观,现要在烟筒外部粘贴瓷砖,请你计算需要多少平方厘米的瓷砖?(结果精确到 , 可用计算工具)
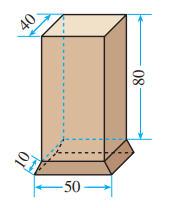
7.
有一堆规格相同的铁制(铁的密度是 ) 六角螺母共重 . 如图, 每一个螺母的底面是正六边形, 边长为 , 内扎直径为 , 高为 , 这堆螺母大约有多少个? (可用计算工具, 取 3.14)

8.
分别以一个直角三角形的斜边、两条直角边所在直线为轴, 其余各边旋转一周形成的曲面围成 3 个几何体. 这 3 个几何体的体积之间有什么关系?
拓广探索
9.
如图是一个奖杯的三视图, 试根据奖杯的三视图计算它的表面积和体积. (可用计算工具,尺寸如图, 单位: 取 3.14 , 结果取整数.)

探究与发现:祖暅原理与柱体、锥体的体积
一、祖暅原理
祖暅(gèng)(5世纪一6世纪), 字景烁, 祖冲之之子, 范阳郡遒县(今河北省涞水县) 人, 南北朝时期的伟大科学家. 祖暅在数学上做出了突出贡献, 他在实践的基础上, 于 5 世纪末提出了下面的体积计算原理: “幂势既同, 则积不容异”. 这就是 “祖暅原理”. “势” 即是高, “幂” 是面积, 祖暅原理用现代语言可以描述为:
定理
夹在两个平行平面之间的两个几何体, 被平行于这两个平面的任意平面所截, 如果截得的两个截面的面积总相等, 那么这两个几何体的体积相等.
例子
如图 1, 夹在平行平面间的两个几何体 (它们的形状可以不同), 被平行于这两个平面的任何一个平面所截, 如果截面(阴影部分)的面积都相等, 那么这两个几何体的体积一定相等.
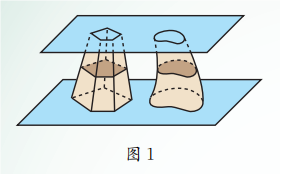
例子
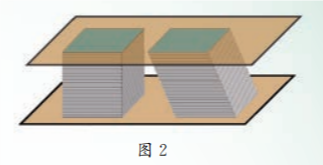
这个原理是非常浅显易懂的. 例如, 取一摞纸堆放在桌面上组成一个几何体 (图 2), 使它倾斜一个角度, 这时几何体的形状发生了改变, 得到了另一个几何体, 但两个几何体的高度没有改变, 每页纸的面积也没有改变, 因而两个几何体的体积相等. 利用这个原理和长方体体积公式, 我们能够求出柱体、锥体、台体和球体的体积.
祖暅给出上面的原理, 要比其他国家的数学家早一千多年. 在欧洲直到 17 世纪,意大利数学家卡瓦列里 (Bonaventura Cavalieri, 1598-1647) 才给出上述结论.
二、柱体、锥体的体积
下面我们用祖暅原理推导柱体和锥体的体积公式.
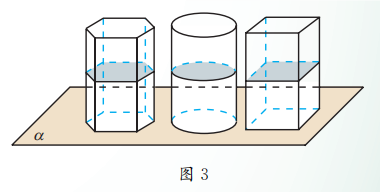
设有底面积都等于 , 高都等于 的任意一个棱柱、一个圆柱和一个长方体, 使它们的下底面在同一平面内(图 3). 根据祖暅原理, 可知它们的体积相等. 由于长方体的体积等于它的底面积乘高, 于是我们得到柱体的体积公式
其中 是柱体的底面积, 是柱体的高.
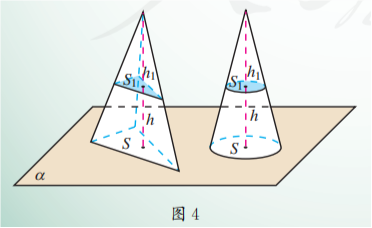
设有底面积都等于 , 高都等于 的两个锥体(例如一个棱锥和一个圆锥),使它们的底面在同一平面内 (图 4). 根据祖暅原理, 可推导出它们的体积相等. 这就是说, 等底面积等高的两个锥体的体积相等.
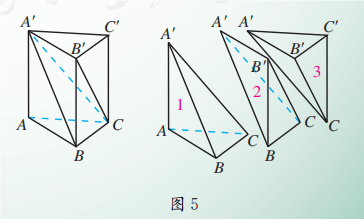
如图 5, 设三棱柱 的底面积(即 的面积)为 , 高(即点 到平面 的距离)为 , 则它的体积为 . 沿平面 和平面 ,将这个三棱柱分割为 3 个三棱锥. 其中三棱锥 1,2 的底面积相等 ), 高也相等 (点 到平面 的距离), 三棱锥 2,3 也有相等的底面积( )和相等的高(点 到平面 的距离). 因此, 这 3 个三棱锥的体积相等, 每个三棱锥的体积是 .
如果三棱锥 (即三棱锥 1) 以 为底, 那么它的底面积是 , 高是 , 而它的体积是 . 这说明三棱锥的体积等于它的底面积乘高的积的三分之一.
定理
事实上, 对于一个任意的锥体, 设它的底面积为 , 高为 , 那么它的体积应等于一个底面积为 , 高为 的三棱锥的体积, 即这个锥体的体积为
这就是锥体的体积公式.
柱体和锥体是两种基本几何体, 它们的体积公式有着广泛的应用.