8.5 空间直线、平面的平行
2024-07-14 22:03:06 新建
在平面几何的学习中, 我们研究过两条直线的位置关系, 重点研究了两条直线平行, 得到了这种特殊位置关系的性质, 以及判定两条直线平行的定理. 类似地, 空间中直线、平面间的平行关系在生产和生活中有着广泛的应用, 也是我们要重点研究的内容. 本节我们研究空间中直线、平面的平行关系, 重点研究这些平行关系的判定和性质.
8.5.1 直线与直线平行
思考
我们知道, 在同一平面内, 不相交的两条直线是平行直线, 并且当两条直线都与第三条直线平行时, 这两条直线互相平行. 在空间中, 是否也有类似的结论?
观察
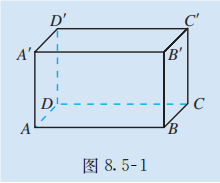
如图 8.5-1, 在长方体 中, , . 与 平行吗?
观察你所在的教室, 你能找到类似的实例吗?
答
可以发现, . 再观察我们所在的教室 (图8.5-2), 黑板边所在直线 和门框所在直线 都平行于墙与墙的交线 , 那么 . 这说明空间中的平行直线具有与平面内的平行直线类似的性质. 我们把它作为基本事实.

基本事实 4
平行于同一条直线的两条直线平行.
基本事实 4 表明,空间中平行于同一条直线的所有直线都互相平行. 它给出了判断空间两条直线平行的依据. 基本事实 4 表述的性质通常叫做平行线的传递性.
例 1
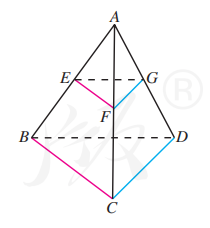
如图 8.5-3, 空间四边形 中, 分别是边 的中点. 求证: 四边形 是平行四边形.
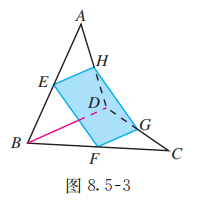
分析:
要证明四边形 是平行四边形, 只需证明它的一组对边平行且相等. 而 分别是 和 的中位线, 从而它们都与 平行且等于 的一半. 应用基本事实 4 , 即可证明 和 平行且相等.
证明:
连接 .
是 的中位线,
, 且 .
同理 , 且 .
和 平行且相等.
四边形 为平行四边形.
思考
在本例中, 如果再加上条件 , 那么四边形 是什么图形?
思考
在平面内, 如果一个角的两边与另一个角的两边分别对应平行, 那么这两个角相等或互补. 在空间中, 这一结论是否仍然成立呢?
答
与平面中的情况类似, 当空间中两个角的两条边分别对应平行时, 这两个角有如图 8.5-4 所示的两种位置.
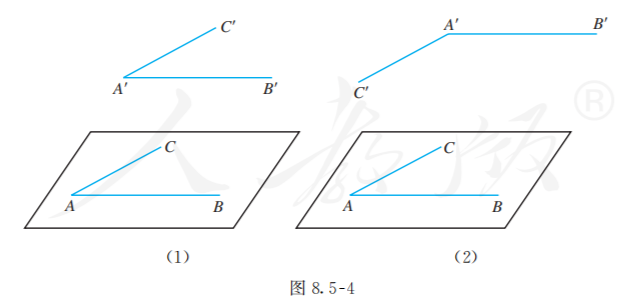
对于图 8.5-4(1), 我们可以构造两个全等三角形, 使 和 是它们的对应角, 从而证明 .
如图 8.5-5, 分别在 和 的两边上截取 和 , 使得 . 连接 .
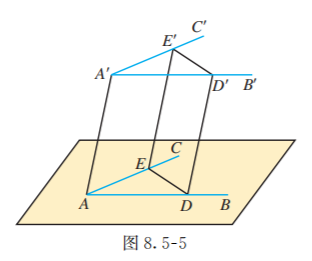
平行且相当于 ,
四边形 是平行四边形.
平行且相当于 .
同理可证 平行且相当于 .
平行且相当于 .
四边形 是平行四边形.
.
.
.
对于图 8.5-4(2) 的情形, 请同学们自己给出证明.
这样, 我们就得到了下面的定理:
定理
如果空间中两个角的两条边分别对应平行, 那么这两个角相等或互补.
练习
1.
如图, 把一张矩形纸片对折几次, 然后打开, 得到的折痕互相平行吗? 为什么?
2.
如图, 在长方体 中, 与棱 平行的棱共有几条? 分别是什么?
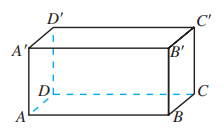
3.
如图, 不共面, 且 平行且相当于 , 平行且相当于 . 求证: .
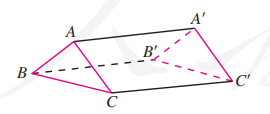
4.
如图, 在四面体 中, 分别为 上的点. 若 , 则 和 有什么关系? 为什么?
8.5.2 直线与平面平行
在直线与平面的位置关系中, 平行是一种非常重要的关系. 它不仅应用广泛, 而且是学习平面与平面平行的基础.
思考
怎样判定直线与平面平行呢? 根据定义, 判定直线与平面是否平行, 只需判定直线与平面有没有公共点. 但是, 直线是无限延伸的, 平面是无限延展的, 如何保证直线与平面没有公共点呢?
观察
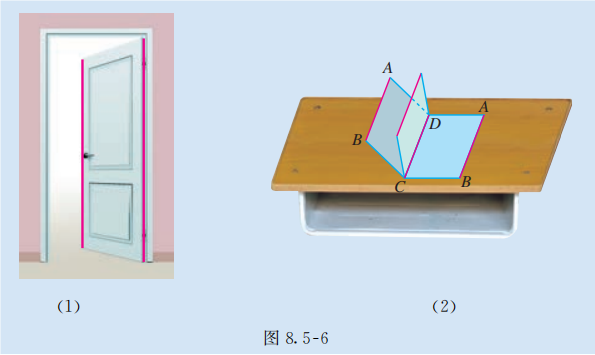
如图 8.5-6(1), 门扇的两边是平行的. 当门扇绕着一边转动时, 另一边与墙面有公共点吗? 此时门扇转动的一边与墙面平行吗?
如图 8.5-6(2), 将一块矩形硬纸板 平放在桌面上, 把这块纸板绕边 转动. 在转动的过程中 ( 离开桌面), 的对边 与桌面有公共点吗? 边 与桌面平行吗?
答
可以发现, 无论门扇转动到什么位置, 因为转动的一边与固定的一边总是平行的, 所以它与墙面是平行的; 硬纸板的边 与 平行, 只要边 紧贴着桌面, 边 转动时就不可能与桌面有公共点, 所以它与桌面平行.
一般地, 我们有直线与平面平行的判定定理:
定理
如果平面外一条直线与此平面内的一条直线平行, 那么该直线与此平面平行.
它可以用符号表示:
例子
这一定理在现实生活中有许多应用. 例如, 安装矩形镜子时, 为了使镜子的上边框与天花板平行, 只需镜子的上边框与天花板和墙面的交线平行, 就是应用了这个判定定理.你还能举出其他一些应用实例吗?
定理告诉我们, 可以通过直线间的平行, 得到直线与平面平行. 这是处理空间位置关系的一种常用方法, 即将直线与平面的平行关系(空间问题)转化为直线间的平行关系 (平面问题).
例 2
求证: 空间四边形相邻两边中点的连线平行于经过另外两边的平面.
已知:
如图 8.5-7, 空间四边形 中, 分别是 的中点.

求证:
平面 .
证明:
连接 .
,
.
又 平面 平面 ,
平面 .
今后要证明一条直线与一个平面平行, 只要在这个平面内找出一条与此直线平行的直线就可以了.
重要过度
前面, 我们利用平面内的直线与平面外的直线平行, 得到了判定平面外的直线与此平面平行的方法, 即得到了一条直线与平面平行的充分条件. 反过来, 如果一条直线与一个平面平行, 能推出哪些结论呢? 这就是要研究直线与平面平行的性质, 也就是研究直线与平面平行的必要条件.
例子
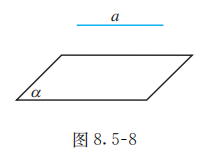
下面我们研究在直线 平行于平面 的条件下, 直线 与平面 内的直线的位置关系.
如图 8.5-8, 由定义, 如果直线 平面 , 那么 与 无公共点, 即 与 内的任何直线都无公共点. 这样, 平面 内的直线与平面 外的直线 只能是异面或者平行的关系. 那么, 在什么条件下, 平面 内的直线与直线 平行呢? 下面我们来分析一下:
假设 与 内的直线 平行, 那么由基本事实的推论 3 , 过直线 有唯一的平面 . 这样, 我们可以把直线 看作过直线 的平面 与平面 的交线. 于是可得如下结论: 过直线 的平面 与平面 相交于 , 则 .
下面, 我们来证明这一结论.
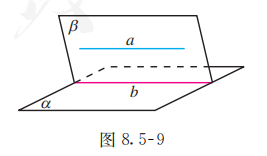
如图 8.5-9, 已知 .
求证: .
证明:
,
.
又 ,
与 无公共点.
又 ,
.
这样, 我们就得到了直线与平面平行的性质定理:
定理
一条直线与一个平面平行, 如果过该直线的平面与此平面相交, 那么该直线与交线平行.
直线与平面平行的性质定理揭示了直线与平面平行中蕴含着直线与直线平行, 这也给出了一种作平行线的方法.
例 3
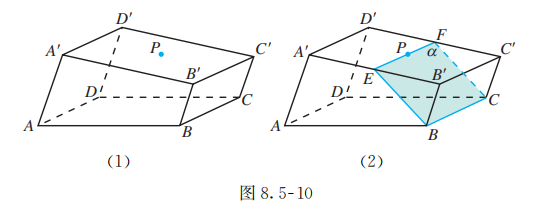
如图 8.5-10 (1) 所示的一块木料中, 棱 平行于面 .
(1) 要经过面 内的一点 和棱 将木料锯开, 在木料表面应该怎样画线?
(2) 所画的线与平面 是什么位置关系?
分析:
要经过面 内的一点 和棱 将木料锯开, 实际上是经过 及 外一点 作截面, 也就需要找出所作的截面与相关平面的交线. 我们可以依据直线与平面平行的性质定理、基本事实 4 和推论 1 画出所需要的线段.
解:
(1) 如图 8.5-10(2), 在平面 内, 过点 作直线 , 使 , 并分别交棱 于点 . 连接 , 则 就是应画的线.
(2) 因为棱 平行于平面 , 平面 与平面 相交于 , 所以 . 由 (1) 知, , 所以 . 而 在平面 内, 在平面 外,所以 平面 .
显然, 都与平面 相交.
练习
1.
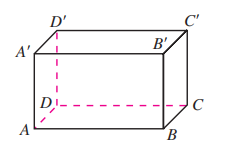
如图, 在长方体 中,
(1) 与 平行的平面是 ;
(2) 与 平行的平面是 ;
(3) 与 平行的平面是 .
2.
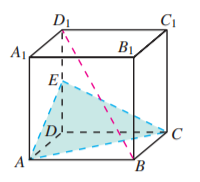
如图, 在正方体 中, 为 的中点, 判断 与平面 的位置关系, 并说明理由.
3.
判断下列命题是否正确, 正确的在括号内画 “ ”, 错误的画 “ ”.
(1) 如果直线 , 那么 平行于经过 的任何平面.
(2) 如果直线 和平面 满足 , 那么 与 内的任何直线平行.
(3) 如果直线 和平面 满足 , 那么 .
(4) 如果直线 和平面 满足 , 那么 .
4.
如图, , 求证 .
8.5.3 平面与平面平行
问
我们首先讨论平面与平面平行的判定问题.
分析
类似于研究直线与平面平行的判定, 我们自然想到要把平面与平面平行的问题转化为直线与平面平行的问题. 根据平面与平面平行的定义, 可以发现, 因为两个平行平面没有公共点, 所以一个平面内的任意一条直线都与另一个平面没有公共点. 也就是说, 如果两个平面平行, 那么一个平面内的任意一条直线都与另一个平面平行. 因为这个定义给出了两个平面平行的充要条件, 所以可以想到, 如果一个平面内的任意一条直线都与另一个平面平行, 那么这两个平面一定平行.
思考
如何判定一个平面内的任意一条直线都平行于另一个平面呢? 有没有更简便的方法?
探究
根据基本事实的推论 2, 3, 过两条平行直线或两条相交直线, 有且只有一个平面. 由此可以想到, 如果一个平面内有两条平行或相交的直线都与另一个平面平行,是否就能使这两个平面平行?
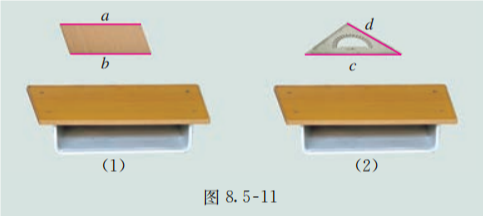
我们可以借助以下两个实例进行观察. 如图 8.5-11(1), 和 分别是矩形硬纸片的两条对边所在直线, 它们都和桌面平行, 那么硬纸片和桌面平行吗? 如图 8.5-11(2), 和 分别是三角尺相邻两边所在直线, 它们都和桌面平行, 那么三角尺和桌面平行吗?
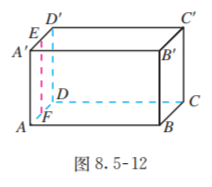
如果一个平面内有两条平行直线与另一个平面平行, 这两个平面不一定平行. 我们借助长方体模型来说明. 如图 8.5-12, 在平面 内画一条与 平行的直线 , 显然 与 都平行于平面 , 但这两条平行直线所在的平面 与平面 相交.
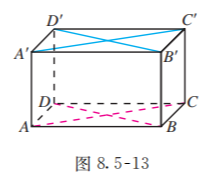
如果一个平面内有两条相交直线与另一个平面平行, 这两个平面是平行的. 如图 8.5-13 的长方体模型中, 平面 内两条相交直线 分别与平面 内两条相交直线 平行. 由直线与平面平行的判定定理可知, 这两条相交直线 都与平面 平行. 此时, 平面 平行于平面 .
思考
两条相交直线和两条平行直线都可以确定一个平面.为什么可以利用两条相交直线判定两个平面平行,而不能利用两条平行直线呢?你能从向量的角度解释吗?
一般地, 我们有如下平面与平面平行的判定定理:
定理
如果一个平面内的两条相交直线与另一个平面平行, 那么这两个平面平行.
它可以用符号表示为 (图 8.5-14)
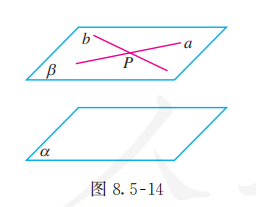
这个定理告诉我们, 可以由直线与平面平行判定平面与平面平行.
例子
如图 8.5-15, 工人师傅将水平仪在桌面上交叉放置两次, 如果水平仪的气泡两次都在中央, 就能判断桌面是水平的, 就是应用了这个判定定理.

例 4
已知正方体 (图 8.5-16), 求证:平面 平面 .
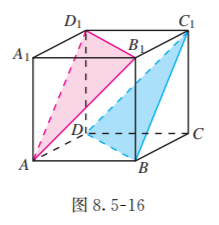
证明:
为正方体,
平行且相等于 , 平行且相等于 ,
平行且相等于 .
四边形 为平行四边形.
.
又 平面 , 平面 ,
平面 .
同理 平面 .
又 ,
平面 平面 .
重要过度
下面我们研究平面与平面平行的性质, 也就是以平面与平面平行为条件, 探究可以推出哪些结论.
根据已有的研究经验, 我们先探究两个平行平面内的直线具有什么位置关系.
如图 8.5-17, 借助长方体模型, 我们看到, 所在的平面 与平面 平行, 所以 与平面 没有公共点. 也就是说, 与平面 内的所有直线没有公共点. 因此, 直线 与平面 内的所有直线要么是异面直线, 要么是平行直线.
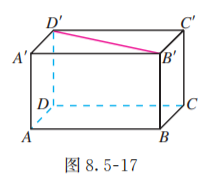
分别位于两个平行平面内的两条直线什么时候平行呢? 我们仍然依据基本事实的推论进行分析:如果 ,且 , 那么过 有且只有一个平面 . 这样, 我们可以把直线 看作平面 与平面 的交线. 于是可以猜想:两个平行平面同时与第三个平面相交, 所得的两条交线平行.
下面, 我们来证明这个结论.
如图 8.5-18, 平面 , 平面 分别与平面 相交于直线 .
,
.
又 ,
没有公共点.
又 同在平面 内,
.
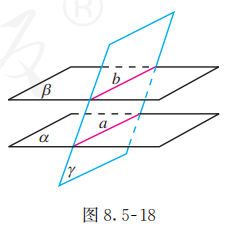
我们把这个结论作为两个平面平行的性质定理.
定理
两个平面平行, 如果另一个平面与这两个平面相交, 那么两条交线平行.
这个定理告诉我们, 可以由平面与平面平行得出直线与直线平行.
思考
如果直线不在两个平行平面内, 或者第三个平面不与这两个平面相交, 以两个平面平行为条件, 你还能得出哪些结论?
例 5
求证: 夹在两个平行平面间的平行线段相等.
如图 8.5-19, , 且 , , 求证 .
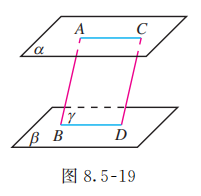
证明:
过平行线 作平面 , 与平面 和 分别相交于 和 .
,
.
又 ,
四边形 是平行四边形.
.
笔记
从本节的讨论可以看到, 由直线与直线平行可以判定直线与平面平行; 由直线与平面平行的性质可以得到直线与直线平行; 由直线与平面平行可以判定平面与平面平行; 由平面与平面平行的定义及性质可以得到直线与平面平行、直线与直线平行. 这种直线、平面之间位置关系的相互转化是立体几何中的重要思想方法.

练习
1.
判断下列命题是否正确. 若正确, 则说明理由; 若错误, 则举出反例.
(1) 已知平面 和直线 , 若 , 则 .
(2) 若一个平面 内两条不平行的直线都平行于另一平面 , 则 .
(3) 平行于同一条直线的两个平面平行.
(4) 平行于同一个平面的两个平面平行.
(5) 一条直线与两个平行平面中的一个相交, 则必与另一个相交.
2.
平面 与平面 平行的充分条件可以是 ( ).
(A) 内有无穷多条直线都与 平行
(B) 直线 , 且直线 不在 内, 也不在 内
(C) 直线 , 直线 , 且
(D) 内的任何一条直线都与 平行
3.
如图, 在正方体 中, 分别是棱 的中点. 求证: 平面 平面 .

4.
如图, 平面 . 判断 与 与 的位置关系, 并说明理由.
习题 8.5
复习巩固
1.
选择题
(1) 若直线 不平行于平面 , 则下列结论成立的是().
(A) 内的所有直线都与 异面
(B) 内不存在与 平行的直线
(C) 内的直线都与 相交
(D) 直线 与平面 有公共点
(2) 如果直线 平面 , 那么过点 且平行于直线 的直线().
(A) 只有一条, 不在平面 内
(B) 有无数条, 不一定在 内
(C) 只有一条, 且在平面 内
(D) 有无数条, 一定在 内
2.
已知平面 和直线 , 且 , 则 与 的位置关系是 .
3.
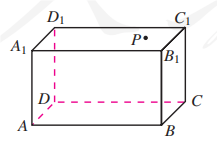
如图, 在长方体木块 中, 面 上有一点 , 怎样过点 画一条直线与棱 平行?
4.
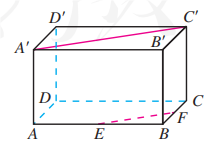
如图, 在长方体 中, 分别是 的中点, 求证 .
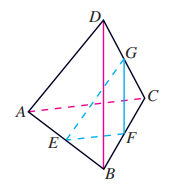
5.
如图, 在四面体 中, 分别是 的中点, 求证:
(1) 平面 ;
(2) 平面 .
6.
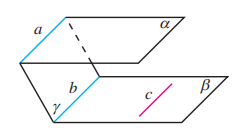
如图, 是异面直线, 画出平面 , 使 , 且 , 并说明理由.
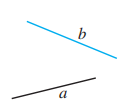
7.
如图, , 求证 .
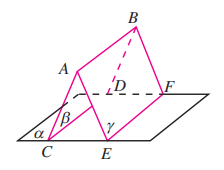
8.
如图, 直线 相交于点 , 求证:平面 平面 .
综合运用
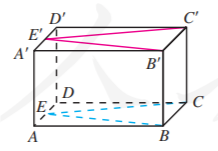
9.
如图, 分别为长方体 的棱 的中点, 求证 .
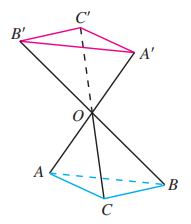
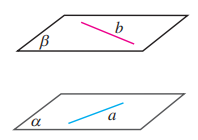
10.
如图, , 求证 .
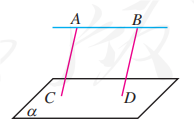
11.
已知平面外的两条平行直线中的一条平行于这个平面, 求证: 另一条也平行于这个平面.
12.
一木块如图所示, 点 在平面 内, 过点 将木块锯开, 使截面平行于直线 和 , 在木块表面应该怎样画线?
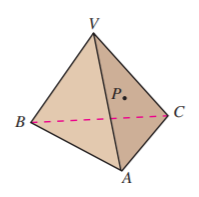
13.
如图, , 直线 与 分别交 于点 和点 , 求证 .
拓广探索
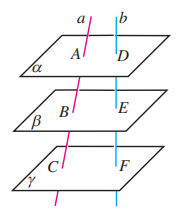
14.
如图, 是异面直线, , 求证 .
15.
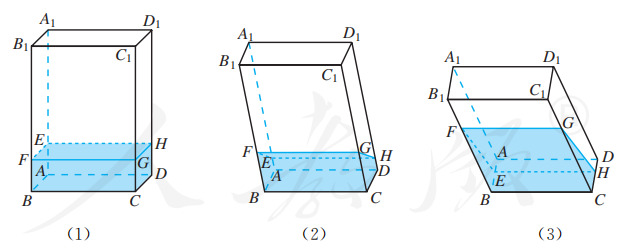
如图, 透明塑料制成的长方体容器 内灌进一些水, 固定容器底面一边 于地面上, 再将容器倾斜. 随着倾斜度的不同, 有下面五个命题:
(1) 有水的部分始终呈棱柱形;
(2) 没有水的部分始终呈棱柱形;
(3) 水面 所在四边形的面积为定值;
(4) 棱 始终与水面所在平面平行;
(5) 当容器倾斜如图 (3) 所示时, 是定值.
其中所有正确命题的序号是 , 为什么?