5.2 三角函数的概念
2024-03-14 22:19:15 新建
在弧度制下, 我们已经将角的范围扩展到全体实数. 下面借助这些知识研究上一节开头提出的问题. 不失一般性,先研究单位圆上点的运动. 现在的任务是:
探究
如图 5.2-1, 单位圆 上的点 以 为起点做逆时针方向旋转, 建立一个数学模型, 刻画点 的位置变化情况.

5.2.1 三角函数的概念
根据研究函数的经验, 我们利用直角坐标系来研究上述问题.
探究
如图 5.2-2, 以单位圆的圆心 为原点, 以射线 为 轴的非负半轴, 建立直角坐标系, 点 的坐标为 , 点 的坐标为 . 射线 从 轴的非负半轴开始, 绕点 按逆时针方向旋转角 , 终止位置为 .
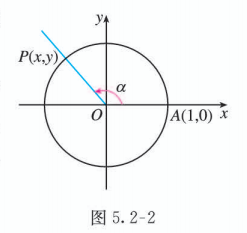
当 时, 点 的坐标是什么? 当 或 时, 点 的坐标又是什么? 它们是唯一确定的吗?
一般地, 任意给定一个角 , 它的终边 与单位圆交点 的坐标能唯一确定吗?
解
利用勾股定理可以发现, 当 时, 点 的坐标是 ; 当 或 时, 点 的坐标分别是 和 . 它们都是唯一确定的.
一般地, 任意给定一个角 , 它的终边 与单位圆交点 的坐标, 无论是横坐标 还是纵坐标 , 都是唯一确定的. 所以, 点 的横坐标 、纵坐标 都是角 的函数.
下面给出这些函数的定义.
定义 三角函数
设 是一个任意角, , 它的终边 与单位圆相交于点 .
(1) 把点 的纵坐标 叫做 的正弦函数 (sine function), 记作 , 即
(2) 把点 的横坐标 叫做 的余弦函数 (cosine function), 记作 , 即
(3) 把点 的纵坐标与横坐标的比值 叫做 的正切, 记作 , 即
可以看出, 当 时, 的终边在 轴上, 这时点 的横坐标 等于 0 , 所以 无意义. 除此之外, 对于确定的角 的值也是唯一确定的. 所以, 也是以角为自变量, 以单位圆上点的纵坐标与横坐标的比值为函数值的函数, 称为正切函数 (tangent function).
我们将正弦函数、余弦函数和正切函数统称为三角函数 (trigonometric function), 通常将它们记为:
正弦函数 ;
余弦函数 ;
正切函数 .
探究
在初中我们学了锐角三角函数, 知道它们都是以锐角为自变量, 以比值为函数值的函数. 设 , 把按锐角三角函数定义求得的锐角 的正弦记为 , 并把按本节三角函数定义求得的 的正弦记为 . 与 相等吗? 对于余弦、正切也有相同的结论吗?
例 1
求 的正弦、余弦和正切值.
解:
在直角坐标系中, 作 (图 5.2-3).
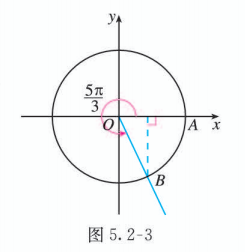
易知 的终边与单位圆的交点坐标为 . 所以,
例 2
如图 5.2-4, 设 是一个任意角, 它的终边上任意一点 (不与原点 重合) 的坐标为 , 点 与原点的距离为 . 求证: .
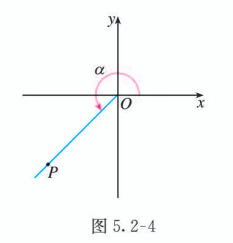
分析:
观察图 5.2-5, 由 , 根据三角函数的定义可以得到证明.
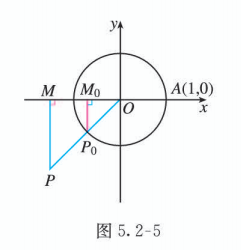
证明:
如图 5.2-5, 设角 的终边与单位圆交于点 .分别过点 作 轴的垂线 , 垂足分别为 , , 则
于是
即
因为 与 同号, 所以
即
同理可得
根据勾股定理, . 由例 2 可知, 只要知道角 终边上任意一点 的坐标,就可以求得角 的各个三角函数值, 并且这些函数值不会随 点位置的改变而改变.
练习
1.
利用三角函数定义, 求 的三个三角函数值.
2.
利用三角函数定义, 求 的三个三角函数值.
3.
已知角 的终边过点 , 求角 的三角函数值.
4.
已知点 在半径为 2 的圆上按顺时针方向做匀速圆周运动, 角速度为 . 求 时点 所在的位置.
学习了三角函数的定义, 接下来研究它们的一些性质.
探究
根据任意角的三角函数定义, 先将正弦、余弦、正切函数在弧度制下的定义域填入表 5.2-1, 再将这三种函数的值在各象限的符号填入图 5.2-6 中的括号.

例 3
求证: 角 为第三象限角的充要条件是
证明:
先证充分性, 即如果(1)(2)式都成立, 那么 为第三象限角.
因为(1)式 成立, 所以 角的终边可能位于第三或第四象限, 也可能与 轴的负半轴重合;
又因为(2)式 成立, 所以 角的终边可能位于第一或第三象限.
因为(1)(2)式都成立, 所以 角的终边只能位于第三象限. 于是角 为第三象限角.
必要性请同学们自己证明.
定理
由三角函数的定义, 可以知道: 终边相同的角的同一三角函数的值相等.
由此得到一组公式:
公式一
其中 .
由公式一可知, 三角函数值有 “周而复始” 的变化规律, 即角 的终边每绕原点旋转一周, 函数值将重复出现.
利用公式一, 可以把求任意角的三角函数值, 转化为求 (或 ) 角的三角函数值.
例 4
确定下列三角函数值的符号, 然后用计算工具验证:
(1) ;
(2) ;
(3) ;
(4) .
解:
(1) 因为 是第三象限角, 所以
(2) 因为 是第四象限角, 所以
(3) 因为 , 而 是第一象限角, 所以
(4) 因为
而 的终边在 轴上, 所以
请同学们自己完成用计算工具验证.
例 5
求下列三角函数值:
(1) (精确到 0.001);
(2) ;
(3) .
解:
(1)
(2) ;
(3) .
可以直接利用计算工具求三角函数的值. 用计算工具求值时要注意设置角的适当的度量制.
练习
1.
填表:
2.
(口答) 设 是三角形的一个内角, 在 中, 哪些有可能取负值?
3.
确定下列三角函数值的符号:
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) .
4.
对于 , , , , 与 , 选择恰当的关系式序号填空:
(1) 角 为第一象限角的充要条件是 ;
(2) 角 为第二象限角的充要条件是 ;
(3) 角 为第三象限角的充要条件是 ;
(4) 角 为第四象限角的充要条件是 .
5.
求下列三角函数值 (可用计算工具, 第 (1) 题精确到 0.000 1):
(1) ;
(2) ;
(3) ;
(4) .
5.2.2 同角三角函数的基本关系
探究
公式一表明终边相同的角的同一三角函数值相等, 那么, 终边相同的角的三个三角函数值之间是否也有某种关系呢?
解
因为三个三角函数值都是由角的终边与单位圆交点所唯一确定的, 所以终边相同的角的三个三角函数值一定有内在联系. 由公式一可知, 我们不妨讨论同一个角的三个三角函数值之间的关系.
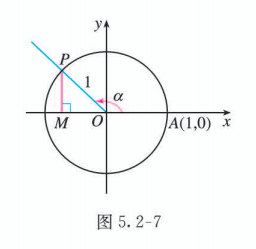
如图 5.2-7, 设点 是角 的终边与单位圆的交点. 过 作 轴的垂线, 交 轴于 , 则 是直角三角形, 而且 . 由勾股定理有
因此, , 即
显然, 当 的终边与坐标轴重合时, 这个公式也成立.
根据三角函数的定义, 当 时, 有
这就是说, 同一个角 的正弦、余弦的平方和等于 1, 商等于角 的正切.
定理 同角三角函数的基本关系
同一个角 的正弦、余弦的平方和等于 1, 商等于角 的正切.
例 6
已知 , 求 的值.
解:
因为 , 所以 是第三或第四象限角.
由 得
如果 是第三象限角, 那么 . 于是
从而
如果 是第四象限角, 那么
例 7
求证: .
证法 1:
由 , 知 , 所以 , 于是
所以, 原式成立.
证法 2:
因为
且 , 所以
定义 三角恒等式
今后, 除特殊注明外,我们假定三角恒等式是在使两边都有意义的情况下的恒等式.
练习
1.
已知 , 且 为第三象限角, 求 的值.
2.
已知 , 求 的值.
3.
已知 , 求 的值(精确到 0.01 ).
4.
化简:
(1) ;
(2) ;
(3) .
5.
求证: .
习题 5.2
复习巩固
1.
用定义法、公式一求下列角的三个三角函数值 (可用计算工具):
(1) ;
(2) ;
(3) ;
(4) .
2.
已知角 的终边上有一点 的坐标是 , 其中 , 求 的值.
3.
计算:
(1) ;
(2) ;
(3) ;
(4) .
4.
化简:
(1) ;
(2) ;
(3) ;
(4) .
5.
确定下列三角函数值的符号:
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) .
6.
(1) 已知 , 且 为第四象限角, 求 的值;
(2) 已知 , 且 为第二象限角, 求 的值;
(3) 已知 , 求 的值;
(4) 已知 , 求 的值(精确到 0.01 ).
综合运用
7.
根据下列条件求函数 的值:
(1) ;
(2) .
8.
确定下列式子的符号:
(1) ;
(2) ;
(3) ;
(4) .
9.
求下列三角函数值 (可用计算工具, 第 (1) (3) (4) 题精确到 0.000 1):
(1) ;
(2) ;
(3) ;
(4) .
10.
求证:
(1) 角 为第二或第三象限角的充要条件是 ;
(2) 角 为第三或第四象限角的充要条件是 ;
(3) 角 为第一或第四象限角的充要条件是 ;
(4) 角 为第一或第三象限角的充要条件是 .
11.
已知 , 求 的值.
12.
已知 , 求 的值.
13.
已知角 的终边不在坐标轴上,
(1) 用 表示 ;
(2) 用 表示 .
14.
求证:
(1) ;
(2) ;
(3) ;
(4) .
15.
已知 , 求 的值.
拓广探索
16.
化简 , 其中 为第二象限角.
17.
从本节的例 7 可以看出, 就是 的一个变形. 你能利用同角三角函数的基本关系推导出更多的关系式吗?
18.
(1) 分别计算 和 的值,你有什么发现?
(2) 任取一个 的值,分别计算 , 你又有什么发现?
(3) 证明: .
阅读与思考
三角学与天文学
三角学的起源、发展与天文学密不可分, 它是天文观察结果推算的一种方法.在 1450 年以前的三角学主要是球面三角, 这不但是因为航海、历法推算以及天文观测等人类实践活动的需要, 而且也因为宇宙的奥秘对人类的巨大吸引力, 这种 “量天的学问” 确实太诱人了. 后来, 由于间接测量、测绘工作的需要而出现了平面三角.
在欧洲, 最早将三角学从天文学中独立出来的数学家是德国人雷格蒙塔努斯 (J. Regiomontanus, 1436-1476). 他在 1464 年完成的 5 卷本的著作《论各种三角形》, 是欧洲第一部独立于天文学的三角学著作, 这部著作首次对三角学做出了完整、独立的阐述. 前 2 卷论述平面三角学, 后 3 卷讨论球面三角学. 前 2 卷中, 他采用印度人的正弦, 即弧的半弦, 明确使用了正弦函数, 讨论了一般三角形的正弦定理, 提出了求三角形边长的代数解法; 后 3 卷中, 给出了球面三角的正弦定理和关于边的余弦定理. 他的工作为三角学在平面与球面几何中的应用奠定了牢固基础, 对 16 世纪的数学家产生了极大影响, 也对哥白尼等一批天文学家产生了很大影响.
由于雷格蒙塔努斯仅仅采用正弦函数和余弦函数, 而且函数值也限定在正数范围内, 因而不能推出应有的三角公式, 导致计算的困难. 后来, 哥白尼的学生雷提库斯 (G. J. Rheticus, 1514-1576) 将传统的弧与弦的关系改进为角的三角函数关系, 把三角函数定义为直角三角形的边长之比, 从而使平面三角学从球面三角学中独立出来. 他还采用了六个函数 (正弦、余弦、正切、余切、正割、余割), 制定了更为精确的正弦、正切、正割表. 这些工作都极大推进了三角学的发展. 实际上, 由于天文学研究的需要, 制定更加精确的三角函数表一直是数学家奋斗的目标, 这大大推动了三角学的发展.
法国数学家韦达(F. Viete,1540-1603)所做的平面三角与球面三角系统化工作, 使得三角学得到进一步发展. 他总结了前人的三角学研究成果, 将解平面直角三角形和斜三角形的公式汇集在一起, 还补充了自己发现的新公式, 如正切公式、和差化积公式等. 他将解斜三角形的问题转化为解直角三角形的问题.对球面直角三角形, 他给出了计算的方法和一套完整的公式及其记忆法则, 并将这套公式表示成了代数形式, 这是非常重要的工作.
16 世纪, 三角学从天文学中分离出来, 成为数学的一个独立分支. 后来, 在微积分、物理学的研究和应用 (如对振动、声音传播等的研究) 中, 三角学又找到了新的用武之地.