6.6 用向量法研究三角形的性质
2024-06-10 22:38:53 新建
我们知道, 向量集数与形于一身, 每一种向量运算都有相应的几何意义. 例如, 向量加法和三角形、平行四边形有密切联系, 数乘向量和平行、图形的相似有密切联系, 而向量的数量积与距离、夹角有密切联系. 向量运算与几何图形性质的这种内在联系, 使我们自然地想到:利用向量运算研究几何图形的性质,是否会更加方便、简捷呢?
在前面的学习中我们看到, “有了运算, 向量的力量无限”. 实际上, 通过向量运算证明某些几何图形的性质, 比平面几何的 “从图形的已知性质推出待证的性质” 简便多了.
例子
例如, 平面几何中证明勾股定理时, 需要添加辅助线、构造正方形等, 不仅复杂, 而且不容易想到. 但用向量法, 我们有:
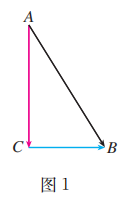
如图 1, 在 Rt 中, . 根据向量的加法法则, 有
所以 .
因为 ,
所以 .
因此 .
这个证明仅仅用到了 “三角形回路(向量加法)” 和数量积运算, 而且证明过程是程序化的, 充分体现了向量运算的作用, 确实简单多了.
下面请同学们以向量为工具, 展开一次数学探究之旅吧.
探究的内容: 用向量法研究三角形的性质
三角形是简单而重要的平面图形, 它是平面几何研究的主角. 初中我们对三角形进行了较深入的研究, 获得了许多性质. 在数学研究中, 常常用新的工具、新的方法对已研究过的对象进行再研究, 这不仅可以站在新的高度重新审视研究对象, 加深对数学对象的认识, 而且可以有所发现. 因此, 以向量为工具对三角形进行再研究是非常有意义的.
- 回顾初中研究三角形的过程, 从研究的思路、内容、方法等角度进行梳理, 并列出已经得到的结论.
- 用向量方法对已证的结论进行证明, 总结用向量方法处理几何问题的基本程序,并与平面几何中的推理论证过程进行比较, 阐述各自的特点.
- 用向量方法证明以往未加证明或你自己新发现的结论.
例子
例如, 在八年级, 我们曾经学过三角形的中线, 知道 “三角形的三条中线相交于一点, 这个交点叫做三角形的重心”. 而物理学知识告诉我们, 重心是物体各部分所受重力的合力的作用点, 形状规则且密度均匀的物体的重心就是它的几何中心. “重心” 是几何学和物理学的共同研究对象, 应该是很重要的, 但我们对它知之甚少. 那么, 它到底有哪些神秘的性质呢?
其实, 从严谨性的角度看, 三角形的两条中线相交于一点是肯定的, 但第三条中线是否经过这个交点是需要证明的. 下面我们就用向量方法来探究它是否成立.
证
如图 2, 在 中, 分别是 的中点, 设 交于一点 , 连接 .
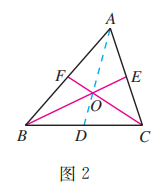
取 为基底, 并设 , 则
所以
又因为 , 所以由平面向量基本定理, 得
解得
所以
因此
于是
这样, 与 共线, 即 是 的 边上的中线, 且过 的交点 .所以, “三角形的三条中线交于一点” 成立.
思考
基底可以有不同的选择, 你可以选择其他基底试一试.
定理
另外, 你有没有发现, . 这表明: 三角形的重心分每条中线为 的两条线段, 即三角形的重心是中线的三等分点.
这样, 我们在证明三角形的三条中线交于一点的过程中, “顺便” 得到了三角形的一个重要性质. 是不是很有趣?
如果把眼光聚焦在三角形的边、外心、中线、重心、角平分线、内心、高、垂心等,你还可以发现更多的性质.
对探究活动的要求
以独立探究和小组合作相结合的方式开展探究活动.
建议按如下步骤完成:
- 小组集体讨论探究方案, 确定研究思路;
- 小组成员各自开展独立探究, 并以专题作业的形式撰写研究报告;
- 小组内进行交流讨论, 完善研究成果, 并形成一份小组研究报告;
- 全班进行成果交流、评价.
研究报告的参考形式
用向量法研究三角形的性质
_ _ _ 年 _ _ _ 班
完成时间: _ _ _
- 本课题组的成员姓名
- 发现的数学结论及发现过程概述
- 证明思路及其形成过程描述
- 结论的证明或否定
- 用向量方法探索几何图形性质的一般步骤
- 收获与体会