2.4 小结
2024-01-24 22:12:02 新建
本章知识结构
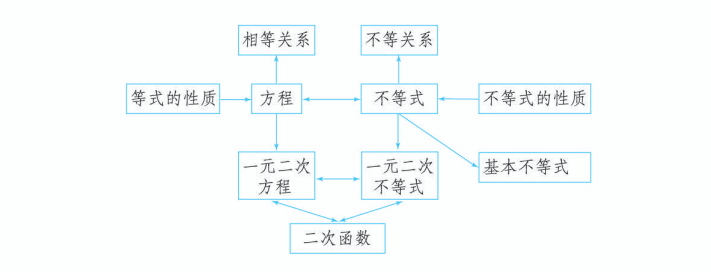
回顾与思考
本章我们类比初中学过的等式与方程学习了不等式的一些知识. 与用方程刻画相等关系类似, 我们用不等式刻画不等关系. 解决不等式问题需要利用不等式的性质, 为此, 在学习关于实数大小关系的基本事实的基础上, 类比等式的性质, 先研究了不等式的一些性质; 接着, 利用不等式的性质研究了基本不等式, 并用基本不等式解决了一些最值问题; 最后, 学习了一元二次不等式,并利用它与二次函数、一元二次方程的联系获得了求解它的一种方法.
关于实数大小关系的基本事实是解决等式、不等式问题的逻辑基础. 不等式与等式之间既有共性又有差异, 所以可以通过类比等式的内容和研究方法,获得关于不等式的内容和研究方法的启发. 其中, “运算中的不变性就是性质”指引我们发现了一些不等式的性质; 等号没有方向性而不等号具有方向性, 这使我们注意到, 在不等式两边同乘一个数(式)时, 所乘数(式)的符号对不等号方向的影响; 等等. 以实数大小关系的基本事实为基础, 先通过类比, 归纳猜想出不等式性质; 再运用逻辑推理证明不等式性质。这个过程不仅可以使我们学习发现数学关系、规律的方法, 而且可以培养我们借助直观理解数学内容、通过逻辑推理证明数学结论的思维习惯.
同样地, 类比用一次函数的观点看一元一次方程、一元一次不等式, 我们得到了以二次函数为纽带, 把一元二次方程、一元二次不等式联系起来的思想方法, 并得到了一种利用函数的零点求一元二次不等式解集的简捷方法.
因此, 类比是发现的引路人, 在今后的学习中我们会经常用到它.
思考
请你带着下面的问题, 复习一下本章内容吧!
- 举出一些蕴含不等关系的实际例子, 并用不等式描述这些不等关系.
- 你能说说用两个实数大小关系的基本事实解决问题时的基本思路吗?
- 在类比等式的基本性质研究不等式的基本性质时, 你认为应特别注意哪些问题?
- 两个正数的大小关系是完全确定的, 但通过运算就会产生非常奇妙的变化, 基本不等式就是其中之一。你还能通过运算(代数变形)得出基本不等式的一些变式吗? 通过对变式的研究, 你有什么体会?
- 用基本不等式解决最大值、最小值问题时, 你认为应注意哪些问题?
- 用函数理解方程和不等式是数学的基本思想方法, 其中函数的图象、零点、图象与 轴的关系等是关键要素. 你能以函数观点看一元二次方程、一元二次不等式为例, 谈谈体会吗?
复习参考题 2
复习巩固
1.
某夏令营有 48 人, 出发前要从 两种型号的帐篷中选择一种. A 型号的帐篷比 型号的少 5 顶. 若只选 型号的, 每顶帐篷住 4 人, 则帐篷不够; 每顶帐篷住 5 人, 则有一顶帐篷没有住满. 若只选 B 型号的, 每顶帐篷住 3 人, 则帐篷不够; 每顶帐篷住 4 人, 则有帐篷多余. 设 A 型号的帐篷有 顶, 用不等式将题目中的不等关系表示出来.
2.
用不等号 “>” 或 “ ” 填空:
(1) 若 , 且 , 则 _ _ _ ;
(2) 若 , 则 _ _ _ ;
(3) 若 , 则 _ _ _ .
3.
(1) 在面积为定值 的扇形中, 半径是多少时扇形的周长最小?
(2) 在周长为定值 的扇形中, 半径是多少时扇形的面积最大?
4.
求下列不等式的解集:
(1) ;
(2) ;
(3) ;
(4) .
综合运用
5.
若 , 且 , 求 的取值范围.
6.
当 取什么值时, 一元二次不等式 对一切实数 都成立?
7.
一般认为, 民用住宅的窗户面积必须小于地板面积, 但窗户面积与地板面积的比应不小于 , 而且这个比值越大, 采光效果越好.
(1) 若一所公寓窗户面积与地板面积的总和为 , 则这所公寓的窗户面积至少为多少平方米?
(2) 若同时增加相同的窗户面积和地板面积, 公寓的采光效果是变好了还是变坏了?
8.
相等关系和不等关系之间具有对应关系: 即只要将一个相等关系的命题中的等号改为不等号就可得到一个相应的不等关系的命题. 请你用类比的方法探索相等关系和不等关系的对应性质,仿照下表列出尽可能多的有关对应关系的命题; 指出所列的对应不等关系的命题是否正确, 并说明理由.
| 相等关系 | 不等关系 | 不等关系 |
|---|---|---|
| 相等关系的命题 | 不等关系的命题 | 判断正误 |
| (1) 若 , 则 | (1) 若 , 则 | 正确 |
| … | ||
| … |
拓广探索
9.
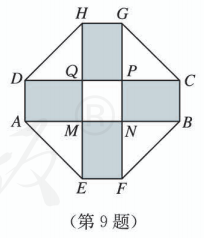
如图, 居民小区要建一座八边形的休闲场所, 它的主体造型平面图是由两个相同的矩形 和 构成的面积为 的十字形地域. 计划在正方形 上建一座花坛, 造价为 4200 元 ;在四个相同的矩形 (图中阴影部分) 上铺花岗岩地坪, 造价为 210 元 ; 再在四个空角 (图中四个三角形) 上铺草坪, 造价为 80 元 . 设总造价为 (单位: 元), 长为 (单位: ). 当 为何值时, 最小? 并求出这个最小值.
10.
购买同一种物品, 可以用两种不同的策略, 第一种是不考虑物品价格的升降, 每次购买这种物品的数量一定; 第二种是不考虑物品价格的升降, 每次购买这种物品所花的钱数一定. 哪种购物方式比较经济? 你能把所得结论作一些推广吗?