7.1 复数的概念
2024-06-12 22:17:38 新建
在解决求判别式小于 0 的实系数一元二次方程根的问题时, 一个自然的想法是, 能否像引进无理数而把有理数集扩充到实数集那样, 通过引进新的数而使实数集得到扩充, 从而使方程变得可解呢? 复数概念的引人与这种想法直接相关.
7.1.1 数系的扩充和复数的概念
从方程的角度看, 负实数能不能开平方, 就是方程 有没有解, 进而可以归结为方程 有没有解.
思考
想一想, 这是为什么?
探究
我们知道, 方程 在实数集中无解. 联系从自然数集到实数集的扩充过程, 你能给出一种方法, 适当扩充实数集, 使这个方程有解吗?
回顾已有的数集扩充过程, 可以看到, 每一次扩充都与实际需求密切相关. 例如, 为了解决正方形对角线的度量,以及 这样的方程在有理数集中无解的问题, 人们把有理数集扩充到了实数集. 数集扩充后, 在实数集中规定的加法运算、乘法运算, 与原来在有理数集中规定的加法运算、乘法运算协调一致, 并且加法和乘法都满足交换律和结合律, 乘法对加法满足分配律.
依照这种思想, 为了解决 这样的方程在实数系中无解的问题, 我们设想引入一个新数 , 使得 是方程 的解, 即使得 .
i 是数学家欧拉(Leonhard Euler, 1707-1783)最早引入的, 它取自 imaginary(想象的, 假想的)一词的词头. .
思考
把新引进的数 添加到实数集中, 我们希望数 和实数之间仍然能像实数那样进行加法和乘法运算, 并希望加法和乘法都满足交换律、结合律, 以及乘法对加法满足分配律. 那么, 实数系经过扩充后, 得到的新数系由哪些数组成呢?
答
依照以上设想, 把实数 与 相乘, 结果记作 ; 把实数 与 相加, 结果记作 . 注意到所有实数以及 都可以写成 的形式, 从而这些数都在扩充后的新数集中.
定义
我们把形如 的数叫做复数(complex number), 其中 叫做虚数单位 (imaginary unit). 全体复数构成的集合 叫做复数集(set of complex numbers). 这样, 方程 在复数集 中就有解 了.
复数通常用字母 表示, 即 . 以后不作特殊说明时, 复数 都有 , 其中的 与 分别叫做复数 的实部(real part)与虚部(imaginary part).
在复数集 中任取两个数 , 我们规定:
与 相等当且仅当 且 .
对于复数 , 当且仅当 时, 它是实数; 当且仅当 时,它是实数 0 ; 当 时, 它叫做虚数(imaginary number); 当 且 时, 它叫做纯虚数.
例子
例如, 都是虚数, 它们的实部分别是 , , 虚部分别是 , 并且其中只有 是纯虚数.
思考
复数集 与实数集 之间有什么关系?
显然, 实数集 是复数集 的真子集, 即 .
这样, 复数 可以分类如下:
复数
复数集、实数集、虚数集、纯虚数集之间的关系, 可用图 7.1-1 表示.

例 1
当实数 取什么值时, 复数 是下列数?
(1) 实数; (2) 虚数; (3) 纯虚数.
分析:
因为 , 所以 都是实数. 由复数 是实数、虚数和纯虚数的条件可以确定 的取值.
解:
(1) 当 , 即 时, 复数 是实数.
(2) 当 ,即 时,复数 是虚数.
(3) 当 , 且 , 即 时, 复数 是纯虚数.
练习
1.
说出下列复数的实部和虚部:
2.
指出下列各数中, 哪些是实数, 哪些是虚数, 哪些是纯虚数. 为什么?
3.
求满足下列条件的实数 的值:
(1) ;
(2) .
7.1.2 复数的几何意义
我们知道, 实数与数轴上的点一一对应, 因此实数可以用数轴上的点来表示. 复数有什么几何意义呢?
思考
根据复数相等的定义, 任何一个复数 都可以由一个有序实数对 唯一确定; 反之也对. 由此你能想到复数的几何表示方法吗?
答
因为任何一个复数 都可以由一个有序实数对 唯一确定, 并且任给一个复数也可以唯一确定一个有序实数对, 所以复数 与有序实数对 是一一对应的. 而有序实数对 与平面直角坐标系中的点是一一对应的, 所以复数集与平面直角坐标系中的点集之间可以建立一一对应关系.
定义
如图 7.1-2, 点 的横坐标是 , 纵坐标是 , 复数 可用点 表示. 这个建立了直角坐标系来表示复数的平面叫做复平面, 轴叫做实轴, 轴叫做虚轴. 显然, 实轴上的点都表示实数; 除了原点外, 虚轴上的点都表示纯虚数.
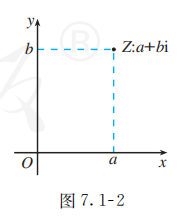
例子
例如, 复平面内的原点 表示实数 0 , 实轴上的点 表示实数 2 , 虚轴上的点 表示纯虚数 , 点 表示复数 等.
定理
按照这种表示方法, 每一个复数, 有复平面内唯一的一个点和它对应; 反过来, 复平面内的每一个点, 有唯一的一个复数和它对应. 由此可知, 复数集 中的数与复平面内的点按如下方式建立了一一对应关系
复数 复平面内的点
这是复数的一种几何意义.
思考
在平面直角坐标系中, 每一个平面向量都可以用一个有序实数对来表示, 而有序实数对与复数是一一对应的. 你能用平面向量来表示复数吗?
定理
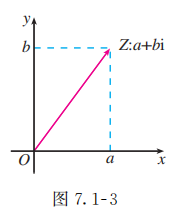
如图 7.1-3, 设复平面内的点 表示复数 , 连接 , 显然向量 由点 唯一确定; 反过来, 点 也可以由向量 唯一确定. 因此, 复数集 中的数与复平面内以原点为起点的向量建立了如下一一对应关系(实数 0 与零向量对应), 即
复数 平面向量
这是复数的另一种几何意义.
在本书的第六章, 我们提到复数的这种几何表示是由韦塞尔在 1797 年提出的. 后来, 阿尔冈出书对此进行讨论, 并得到高斯的认同, 因此这种几何表示也称阿尔冈图 (Argand diagram). 正是这种直观的几何表示, 揭开了复数的神秘的、不可思议的 “面纱”, 确立了复数在数学中的地位.
为方便起见, 我们常把复数 说成点 或说成向量 , 并且规定, 相等的向量表示同一个复数.
定义
图 7.1-3 中向量 的模叫做复数 的模 (modulus of a complex number) 或绝对值, 记作 或 . 即
其中 .
如果 , 那么 是一个实数 , 它的模就等于 ( 的绝对值).
例 2
设复数 .
(1) 在复平面内画出复数 对应的点和向量;
(2) 求复数 的模, 并比较它们的模的大小.
解:
(1) 如图 7.1-4, 复数 对应的点分别为 , 对应的向量分别为
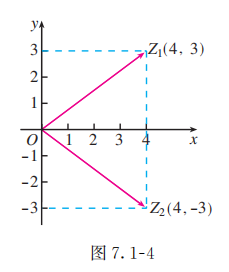
(2) ,
.
所以 .
思考
点 有怎样的关系?
定义 共轭复数
一般地, 当两个复数的实部相等, 虚部互为相反数时, 这两个复数叫做互为共轭复数 (conjugate complex number). 虚部不等于 0 的两个共轭复数也叫做共轭虚数. 复数 的共轴复数用 表示, 即如果 , 那么 .
思考
如果 是共轨复数, 那么在复平面内它们所对应的点有怎样的关系?
例 3
设 , 在复平面内 对应的点为 , 那么满足下列条件的点 的集合是什么图形?
(1) ;
(2) .
解:
(1) 由 得, 向量 的模等于 1 , 所以满足条件 的点 的集合是以原点 为圆心, 以 1 为半径的圆.
(2) 不等式 可化为不等式
不等式 的解集是圆 的内部所有的点组成的集合, 不等式 的解集是圆 外部所有的点组成的集合, 这两个集合的交集, 就是上述不等式组的解集, 也就是满足条件 的点 的集合. 容易看出, 所求的集合是以原点 为圆心, 以 1 及 2 为半径的两个圆所夹的圆环, 但不包括圆环的边界 (图 7.1-5).
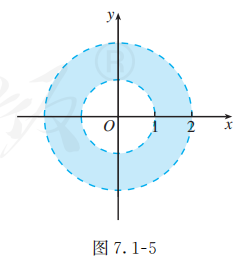
练习
1.
说出图中复平面内各点所表示的复数 (每个小方格的边长为 1 ).
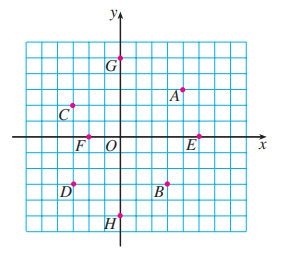
2.
在复平面内, 描出表示下列复数的点:
(1) ;
(2) ;
(3) ;
(4) ;
(5) 5 ;
(6) .
3.
已知复数 ,
(1) 在复平面内画出这些复数对应的向量;
(2) 求这些复数的模.
习题 7.1
复习巩固
1.
符合下列条件的复数一定存在吗? 若存在, 请举出例子; 若不存在, 请说明理由.
(1) 实部为 的虚数;
(2) 虚部为 的虚数;
(3) 虚部为 的纯虚数.
2.
当实数 取什么值时,复数 是下列数?
(1) 实数;
(2) 虚数;
(3) 纯虚数.
3.
求适合下列方程的实数 与 的值:
(1) ;
(2) .
4.
如果 是复平面内表示复数 的点, 分别指出在下列条件下点 的位置.
(1) ;
(2) ;
(3) ;
(4) .
5.
求复数 及 的模, 并比较它们的模的大小.
综合运用
6.
当实数 取什么值时, 复平面内表示复数 的点分别满足下列条件?
(1) 位于第四象限;
(2) 位于第一象限或第三象限;
(3) 位于直线 上.
7.
在复平面内, 是原点, 向量 对应的复数是 .
(1) 如果点 关于实轴的对称点为点 , 求向量 对应的复数;
(2) 如果 (1) 中点 关于虚轴的对称点为点 , 求点 对应的复数.
8.
设 , 在复平面内 对应的点为 , 那么满足下列条件的点 的集合是什么图形?
(1) ;
(2) .
9.
如果复数 的实部为正数, 虚部为 3 , 那么在复平面内, 复数 对应的点应位于怎样的图形上?
拓广探索
10.
已知复数 的虚部为 , 在复平面内复数 对应的向量的模为 2 , 求这个复数 .
11.
在复平面内指出与复数 对应的点 , . 判断这 4 个点是否在同一个圆上, 并证明你的结论.