4.2 指数函数
2024-02-11 22:11:39 新建
对于幂 , 我们已经把指数 的范围拓展到了实数. 上一章学习了函数的概念和基本性质, 通过对幂函数的研究, 进一步了解了研究一类函数的过程和方法. 下面继续研究其他类型的基本初等函数.
4.2.1 指数函数的概念
问题 1
随着中国经济高速增长, 人民生活水平不断提高, 旅游成了越来越多家庭的重要生活方式. 由于旅游人数不断增加, A, B 两地景区自 2001 年起采取了不同的应对措施, A 地提高了景区门票价格, 而 B 地则取消了景区门票. 表 4.2-1 给出了 A, B 两地景区 2001 年至 2015 年的游客人次以及逐年增加量.
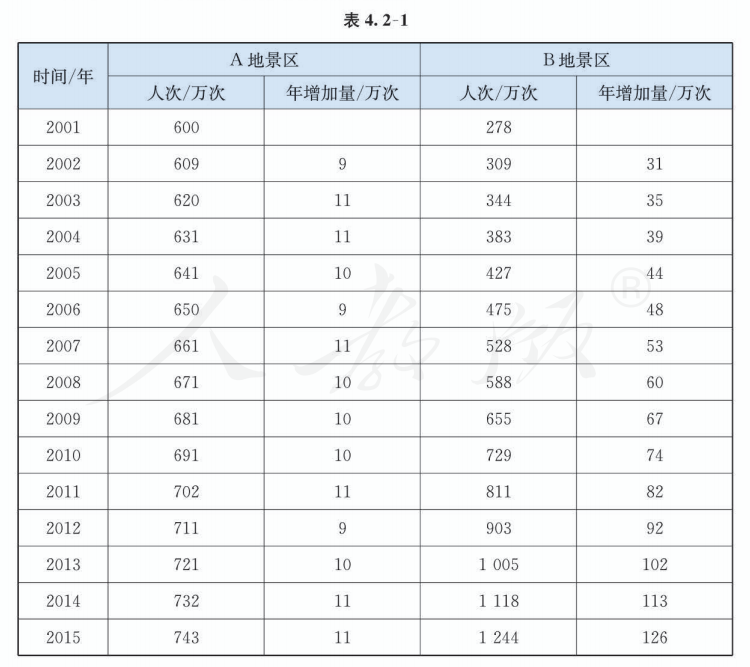
比较两地景区游客人次的变化情况, 你发现了怎样的变化规律?
解
为了有利于观察规律, 根据表 4.2-1, 分别画出 A, B 两地景区采取不同措施后的 15 年游客人次的图象 (图 4.2-1 和图 4.2-2).
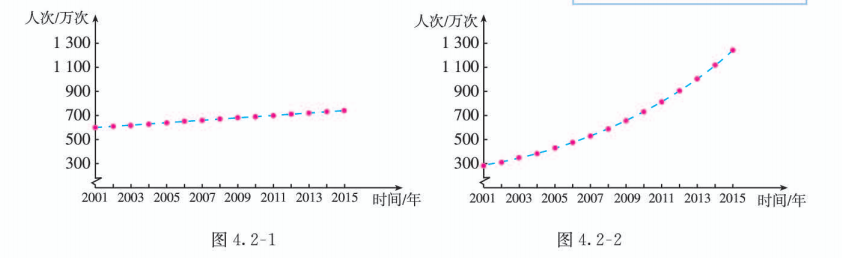
为了便于观察, 可以先根据表格中的数据描点, 然后用光滑的曲线将离散的点连起来.
观察图象和表格, 可以发现, A 地景区的游客人次近似于直线上升 (线性增长), 年增加量大致相等 (约为 10 万次); 地景区的游客人次则是非线性增长, 年增加量越来越大, 但从图象和年增加量都难以看出变化规律.
探究
我们知道, 年增加量是对相邻两年的游客人次做减法得到的. 能否通过对 地景区每年的游客人次做其他运算发现游客人次的变化规律呢? 请你试一试.
做减法可以得到游客人次的年增加量, 做除法可以得到游客人次的年增长率. 增加量、增长率是刻画事物变化规律的两个很重要的量.
解
从 2002 年起, 将 地景区每年的游客人次除以上一年的游客人次, 可以得到
结果表明, 地景区的游客人次的年增长率都约为 , 是一个常数.
像这样, 增长率为常数的变化方式, 我们称为指数增长. 因此, B 地景区的游客人次近似于指数增长.
显然, 从 2001 年开始, B 地景区游客人次的变化规律可以近似描述为:
1 年后, 游客人次是 2001 年的 倍;
2 年后, 游客人次是 2001 年的 倍;
3 年后, 游客人次是 2001 年的 倍;
年后, 游客人次是 2001 年的 倍.
如果设经过 年后的游客人次为 2001 年的 倍, 那么
这是一个函数, 其中指数 是自变量.
问题 2
当生物死亡后, 它机体内原有的碳 14 含量会按确定的比率衰减(称为衰减率), 大约每经过 5730 年衰减为原来的一半, 这个时间称为 “半衰期”. 按照上述变化规律, 生物体内碳 14 含量与死亡年数之间有怎样的关系?
设死亡生物体内碳 14 含量的年衰减率为 , 如果把刚死亡的生物体内碳 14 含量看成 1 个单位, 那么
死亡 1 年后, 生物体内碳 14 含量为 ;
死亡 2 年后, 生物体内碳 14 含量为 ;
死亡 3 年后, 生物体内碳 14 含量为 ;
死亡 5730 年后, 生物体内碳 14 含量为 .
根据已知条件, , 从而 , 所以 .
设生物死亡年数为 , 死亡生物体内碳 14 含量为 , 那么 , 即
这也是一个函数, 指数 是自变量. 死亡生物体内碳 14 含量每年都以 的衰减率衰减. 像这样, 衰减率为常数的变化方式, 我们称为指数衰减. 因此, 死亡生物体内碳 14 含量呈指数衰减.
如果用字母 代替上述 ① ② 两式中的底数 1.11 和 , 那么函数 和 就可以表示为
的形式, 其中指数 是自变量, 底数 是一个大于 0 且不等于 1 的常量.
定义 指数函数
一般地, 函数 , 且 叫做指数函数(exponential function), 其中指数 是自变量, 定义域是 .
例 1
已知指数函数 , 且 , 且 , 求 , 的值.
分析:
要求 的值, 应先求出 的解析式, 即先求 的值.
解:
因为 , 且 , 则 , 解得 , 于是
所以, .
例 2
(1) 在问题 1 中, 如果平均每位游客出游一次可给当地带来 1000 元门票之外的收入, A 地景区的门票价格为 150 元, 比较这 15 年间 A, B 两地旅游收入变化情况.
(2) 在问题 2 中,某生物死亡 10000 年后,它体内碳 14 的含量衰减为原来的百分之几?
解:
(1) 设经过 年, 游客给 两地带来的收人分别为 和 , 则
利用计算工具可得,
当 时, .
当 时, .
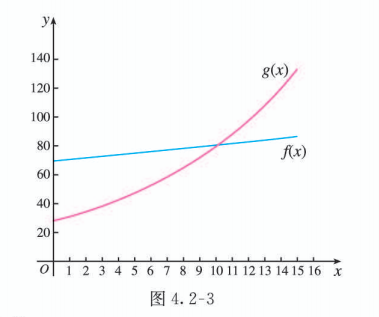
结合图 4.2-3 可知:
当 时, ,
当 时, .
当 时, .
这说明, 在 2001 年, 游客给 地带来的收人比 地多 412000 万元; 随后 10 年, 虽然 , 但 的增长速度大于 ; 根据上述数据, 并考虑到实际情况, 在 2011 年 3 月某个时刻就有 , 这时游客给 地带来的收入和 地差不多; 此后, , 游客给 地带来的收入超过了 地; 由于 增长得越来越快, 在 2015 年, 地的收人已经比 地多 347303 万元了.
(2) 设生物死亡 年后, 它体内碳 14 含量为 .
如果把刚死亡的生物体内碳 14 含量看成 1 个单位, 那么
当 时, 利用计算工具求得 .
所以, 生物死亡 10000 年后, 它体内碳 14 含量衰减为原来的约 .
在实际问题中, 经常会遇到类似于例 2(1) 的指数增长模型: 设原有量为 , 每次的增长率为 , 经过 次增长, 该量增长到 , 则 . 形如 ,且 , 且 的函数是刻画指数增长或指数衰减变化规律的非常有用的函数模型.
练习
1.
下列图象中, 有可能表示指数函数的是 ( ).

2.
已知函数 , 且 , 求函数 的一个解析式.
3.
在某个时期, 某湖泊中的蓝藻每天以 的增长率呈指数增长, 那么经过 30 天, 该湖泊的蓝藻会变为原来的多少倍? (可以使用计算工具)
阅读与思考
放射性物质的衰减
本节问题 2 中的碳 14 是一种著名的放射性物质, 像铀 235 、锶 90 、碘 131 、铯 137、镭 226 等也都是放射性物质. 放射性物质是指那些能自然地向外辐射能量, 发出射线的物质. 在一个给定的单位时间内, 放射性物质的质量会按某个衰减率衰减. 一般是用放射性物质质量衰减一半所用的时间来描述其衰减情况, 这个时间被称做半衰期. 那么连续两个半衰期是否就是一个 “全衰期”(放射性物质质量衰减为 0 所用的时间)?
实际上, 在连续两个半衰期里, 放射性物质将衰减为原有质量的 .所以, 连续两个半衰期并非是一个全衰期.
在问题 2 中, 我们知道碳 14 的半衰期为 5730 年, 如果 是碳 14 的初始质量, 那么经过 年后, 碳 14 所剩的质量 .
一般地, 如果某物质的半衰期为 , 那么经过时间 后, 该物质所剩的质量 , 其中 是该物质的初始质量. 你能说明理由吗?
如果某函数呈指数增长, 那么称函数值增长为原来两倍所用的时间为 “倍增期”. 你能通过上网查询, 给出一个倍增的指数函数模型实例吗?
4.2.2 指数函数的图象和性质
下面我们类比研究幂函数性质的过程和方法, 进一步研究指数函数. 首先画出指数函数的图象, 然后借助图象研究指数函数的性质.
过程
先从简单的函数 开始.
请同学们完成 的对应值表 4.2-2, 并用描点法画出函数 的图象 (图 4.2-4).
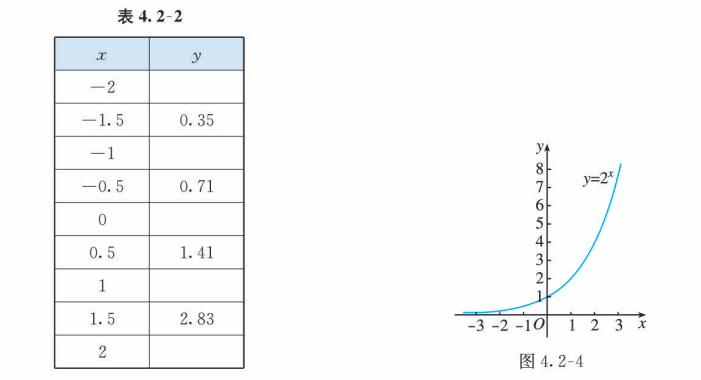
为了得到指数函数 , 且 的性质, 我们还需要画出更多的具体指数函数的图象进行观察.
探究
画出函数 的图象, 并与函数 的图象进行比较, 它们有什么关系?能否利用函数 的图象, 画出函数 的图象?
解
因为 , 点 与点 关于 轴对称, 所以函数 图象上任意一点 关于 轴的对称点 都在函数 的图象上, 反之亦然. 由此可知, 底数互为倒数的两个指数函数的图象关于 轴对称. 根据这种对称性, 就可以利用一个函数的图象, 画出另一个函数的图象, 比如利用函数 的图象, 画出 的图象 (图 4.2-5).
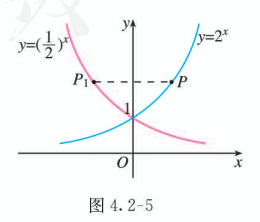
探究
选取底数 , 且 的若干个不同的值, 在同一直角坐标系内画出相应的指数函数的图象. 观察这些图象的位置、公共点和变化趋势, 它们有哪些共性? 由此你能概括出指数函数 , 且 的值域和性质吗?
解
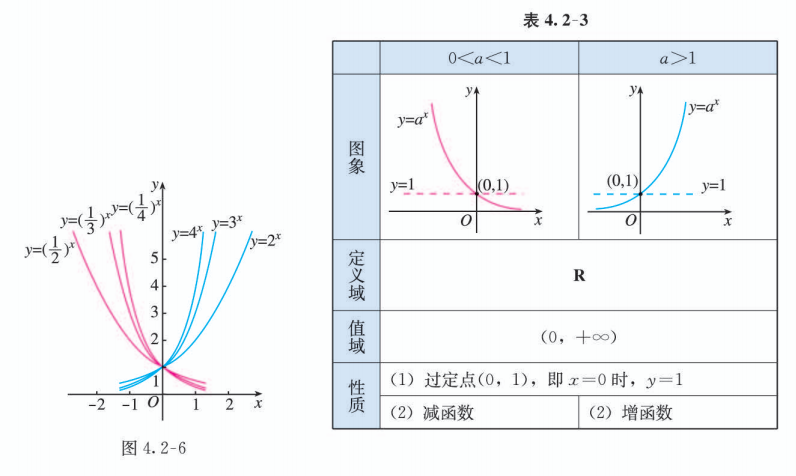
如图 4.2-6, 选取底数 的若干值, 用信息技术画图, 发现指数函数 的图象按底数 的取值, 可分为 和 两种类型. 因此, 指数函数的性质也可以分 和 两种情况进行研究.
一般地, 指数函数的图象和性质如表 4.2-3 所示.
例 3
比较下列各题中两个值的大小:
(1) ;
(2) ;
(3) .
分析:
对于 (1) (2), 要比较的两个值可以看作一个指数函数的两个函数值, 因此可以直接利用指数函数的单调性进行比较; 对于 (3), 和 不能看作某一个指数函数的两个函数值. 可以利用函数 和 的单调性, 以及 “ 时, ”这条性质把它们联系起来.
解:
(1) 和 可看作函数 当 分别取 2.5 和 3 时所对应的两个函数值.
因为底数 , 所以指数函数 是增函数.
因为 , 所以 .
(2) 同 (1) 理, 因为 , 所以指数函数 是减函数.
因为 , 所以 .
(3) 由指数函数的性质知
所以 .
由例 3 可以看到, 利用指数函数的单调性, 通过自变量的大小关系可以判断相应函数值的大小关系.
例 4
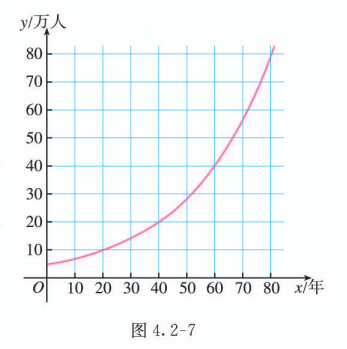
如图 4.2-7, 某城市人口呈指数增长.
(1) 根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2) 该城市人口从 80 万人开始, 经过 20 年会增长到多少万人?
分析:
(1) 因为该城市人口呈指数增长,而同一指数函数的倍增期是相同的, 所以可以从图象中选取适当的点计算倍增期.
(2) 要计算 20 年后的人口数, 关键是要找到 20 年与倍增期的数量关系.
解:
(1) 观察图 4.2-7, 发现该城市人口经过 20 年约为 10 万人, 经过 40 年约为 20 万人, 即由 10 万人口增加到 20 万人口所用的时间约为 20 年, 所以该城市人口每翻一番所需的时间约为 20 年.
(2) 因为倍增期为 20 年, 所以每经过 20 年,人口将翻一番. 因此, 从 80 万人开始, 经过 20 年, 该城市人口大约会增长到 160 万人.
练习
1.
在同一直角坐标系中画出函数 和 的图象, 并说明它们的关系.
2.
比较下列各题中两个值的大小:
(1) ;
(2) ;
(3) .
3.
体内癌细胞初期增加得很缓慢, 但到了晚期就急剧增加, 画一幅能反映体内癌细胞数量随时间变化的示意图.
习题 4.2
复习巩固
1.
求下列函数的定义域:
(1) ;
(2) ;
(3) ;
(4) .
2.
一种产品原来的年产量是 件, 今后 年内, 计划使产量平均每年比上一年增加 , 写出年产量 (单位: 件) 关于经过的年数 的函数解析式.
3.
比较满足下列条件的 的大小:
(1) ;
(2) ;
(3) ;
(4) .
4.
设函数 , 且 .
(1) 求函数 的增长率 ;
(2) 求 的值.
综合运用
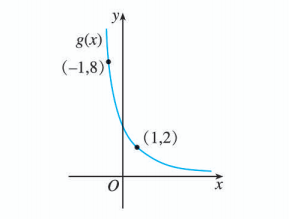
5.
求下列函数可能的一个解析式:
(1) 函数 的数据如下表:

(2) 函数 的图象如下:
6.
比较下列各题中两个值的大小:
(1) ;
(2) ;
(3) ;
(4) .
7.
当死亡生物组织内碳 14 的含量不足死亡前的千分之一时, 用一般的放射性探测器就测不到碳 14 了. 如果死亡生物组织内的碳 14 经过九个 “半衰期” 后, 那么用一般的放射性探测器能测到碳 14 吗?
8.
按复利计算利息的一种储蓄, 本金为 (单位: 元), 每期利率为 , 本利和为 (单位: 元), 存期数为 .
(1) 写出本利和 关于存期数 的函数解析式;
(2) 如果存人本金 1000 元, 每期利率为 , 试计算 5 期后的本利和.
复利是一种计算利息的方法, 即把前一期的利息和本金加在一起算作本金, 再计算下一期的利息.我国现行定期储蓄中的自动转存业务就是类似复利计算的储蓄.
拓广探索
9.
已知函数 的图象过原点, 且无限接近直线 但又不与该直线相交.
(1) 求该函数的解析式, 并画出图象;
(2) 判断该函数的奇偶性和单调性.
10.
已知 , 且 ,
(1) 讨论函数 和 的单调性.
(2) 如果 , 那么 的取值范围是多少?
信息技术应用
探究指数函数的性质
函数图象是研究函数性质和进一步理解其概念的重要载体. 利用信息技术强大的作图以及对图象和数据的分析功能, 例如函数图象的动态演示, 引起图象变化的关键因素分析, 图象的局部放大和缩小等, 有利于我们观察函数的整体变化情况, 并考察其中的细节, 从而获得大量关于函数特点的信息. 这将极大地方便我们归纳、概括函数的性质以及发现不同函数之间的区别与联系. 下面,我们就利用信息技术来探究指数函数的性质.
- 用信息技术绘制函数 , 且 的图象. 由于底数 可取大于 0 且不等于 1 的所有实数, 所以不妨用一端固定于 轴的水平线段 的长度来表示底数 的值, 即点 的横坐标 显示的就是 的取值.
- 如图 1, 从左向右拖动点 , 则 的值逐渐增大. 当 的值越来越接近于 1 时, 图象就越来越接近于直线 ; 当 时, 图象就是直线 ; 继续向右拖动点 , 如图 2, 图象发生了变化, 随着 的值逐渐增大, 在第一象限内, 图象越来越接近于 轴, 在第二象限内, 图象越来越接近于 轴.
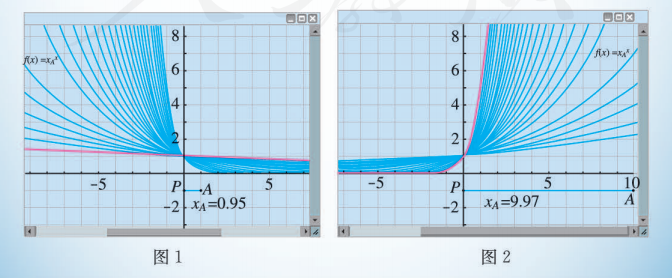
- 根据图 1 和图 2, 可以容易地发现指数函数的下列性质:
(1) 所有函数的图象都过点 .
(2) 所有函数的定义域都是 , 值域都是 .
(3) 在图 1 中, 当 时, 函数图象均呈下降趋势, 即函数为减函数;在图 2 中, 当 时, 函数图象均呈上升趋势, 即函数为增函数.
接下来, 请你思考和探究下列问题:
- 继续观察图 1 和图 2, 当自变量 取同一个数时, 对应的函数值 的大小关系是什么,你从中发现了什么规律?
- 类似地, 你可以利用信息技术绘制幂函数 的图象, 通过改变 的大小, 认识幂函数的变化规律.