2.1 等式性质与不等式性质
2024-01-16 23:31:41 新建
在现实世界和日常生活中, 大量存在着相等关系和不等关系, 例如多与少、大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过或不少于等. 类似于这样的问题, 反映在数量关系上, 就是相等与不等. 相等用等式表示, 不等用不等式表示.
问题 1
你能用不等式或不等式组表示下列问题中的不等关系吗?
(1) 某路段限速 ;
(2) 某品牌酸奶的质量检查规定, 酸奶中脂肪的含量 应不少于 , 蛋白质的含量 应不少于 ;
(3) 三角形两边之和大于第三边、两边之差小于第三边;
(4) 连接直线外一点与直线上各点的所有线段中, 垂线段最短.
解
对于 (1), 设在该路段行驶的汽车的速度为 , “限速 ” 就是 的大小不能超过 40 , 于是 .
对于 (2), 由题意, 得
对于 (3), 设 的三条边为 , 则 , .
对于 (3), 你能写出其他的可能情况吗?
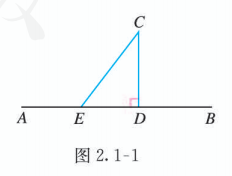
对于 (4), 如图 2.1-1, 设 是直线 外的任意一点, 垂直于 , 垂足为 是直线 上不同于 的任意一点, 则 .
以上我们根据实际问题所蕴含的不等关系抽象出了不等式. 接着, 就可以用不等式研究相应的问题了.
问题 2
某种杂志原以每本 2.5 元的价格销售, 可以售出 8 万本. 据市场调查, 杂志的单价每提高 0.1 元, 销售量就可能减少 2000 本. 如何定价才能使提价后的销售总收入不低于 20 万元?
分析
设提价后每本杂志的定价为 元, 则销售总收人为 万元. 于是,不等关系 “销售总收人不低于 20 万元” 可以用不等式表示为
求出不等式(1)的解集, 就能知道满足条件的杂志的定价范围.
如何解不等式(1)呢? 与解方程要用等式的性质一样, 解不等式要用不等式的性质. 为此, 我们需要先研究不等式的性质.
实际上, 在初中我们已经通过具体实例归纳出了一些不等式的性质. 那么, 这些性质为什么是正确的? 还有其他不等式的性质吗? 回答这些问题要用到关于两个实数大小关系的基本事实.
由于数轴上的点与实数一一对应, 所以可以利用数轴上点的位置关系来规定实数的大小关系: 如图 2.1-2, 设 是两个实数, 它们在数轴上所对应的点分别是 . 那么, 当点 在点 的左边时, ; 当点 在点 的右边时, .

定理
关于实数 大小的比较, 有以下基本事实:
如果 是正数, 那么 ; 如果 等于 0 , 那么 ; 如果 是负数,那么 . 反过来也对.
这个基本事实可以表示为
从上述基本事实可知, 要比较两个实数的大小, 可以转化为比较它们的差与 0 的大小.
0 是正数与负数的分界点, 它为实数比较大小提供了“标杆”.
例 1
比较 和 的大小.
分析:
通过考察这两个多项式的差与 0 的大小关系, 可以得出它们的大小关系.
解:
因为
所以
这里, 我们借助多项式减法运算, 得出了一个明显大于 0 的数 (式). 这是解决不等式问题的常用方法.
探究
图 2.1-3 是在北京召开的第 24 届国际数学家大会的会标, 会标是根据中国古代数学家赵爽的弦图设计的, 颜色的明暗使它看上去像一个风车, 代表中国人民热情好客. 你能在这个图中找出一些相等关系和不等关系吗?

解
将图 2.1-3 中的 “风车” 抽象成图 2.1-4.
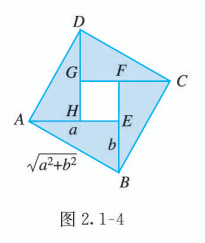
在正方形 中有 4 个全等的直角三角形. 设直角三角形的两条直角边的长为 , , 那么正方形的边长为 . 这样, 4 个直角三角形的面积和为 , 正方形的面积为 . 由于正方形 的面积大于 4 个直角三角形的面积和, 我们就得到了一个不等式
当直角三角形变为等腰直角三角形, 即 时, 正方形 缩为一个点, 这时有
于是就有 .
定理
一般地, , 有
当且仅当 时, 等号成立.
证明
事实上, 利用完全平方公式, 得
因为 , 当且仅当 时, 等号成立,所以 . 因此, 由两个实数大小关系的基本事实, 得 , 当且仅当 时, 等号成立.
练习
1.
用不等式或不等式组表示下面的不等关系:
(1) 某高速公路规定通过车辆的车货总高度 (单位: m) 从地面算起不能超过 ;
(2) 与 的和是非负实数;
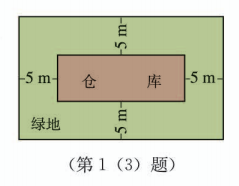
(3) 如图, 在一个面积小于 的矩形地基的中心位置上建造一个仓库, 仓库的四周建成绿地, 仓库的长 (单位: m) 大于宽 (单位: ) 的 4 倍.
2.
比较 和 的大小.
3.
已知 , 证明 .
关于两个实数大小关系的基本事实为研究不等式的性质奠定了基础. 那么, 不等式到底有哪些性质呢?
因为不等式与等式一样, 都是对大小关系的刻画, 所以我们可以从等式的性质及其研究方法中获得启发.
思考
请你先梳理等式的基本性质, 再观察它们的共性. 你能归纳一下发现等式基本性质的方法吗?
定理
等式有下面的基本性质:
性质 1 如果 , 那么 ;
性质 2 如果 , 那么 ;
性质 3 如果 , 那么 ;
性质 4 如果 , 那么 ;
性质 5 如果 , 那么 .
可以发现, 性质 1,2 反映了相等关系自身的特性, 性质 是从运算的角度提出的, 反映了等式在运算中保持的不变性.
运算中的不变性就是性质.
探究
类比等式的基本性质, 你能猜想不等式的基本性质, 并加以证明吗?
类比等式的性质 1,2 , 可以猜想不等式有如下性质:
性质 1
如果 , 那么 ; 如果 , 那么 . 即
性质 2
如果 , 那么 . 即
证明性质 2:
由两个实数大小关系的基本事实知
类比等式的性质 , 可以猜想不等式还有如下性质:
性质 3
如果 , 那么 .
这就是说, 不等式的两边都加上同一个实数, 所得不等式与原不等式同向.
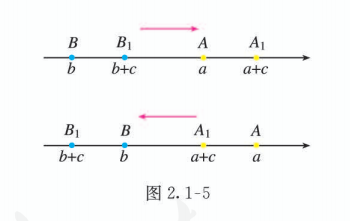
如图 2.1-5, 把数轴上的两个点 与 同时沿相同方向移动相等的距离, 得到另两个点 与 与 和 与 的左右位置关系不会改变. 用不等式的语言表示, 就是上述性质 3 .
思考
从不同角度表述不等式的性质, 可以加深理解.对其他不等式的性质,你能用文字语言表述吗?
推论
由性质 3 可得,
这表明, 不等式中任何一项可以改变符号后移到不等号的另一边.
性质 4
如果 , 那么 ; 如果 , 那么 .
这就是说, 不等式两边同乘一个正数, 所得不等式与原不等式同向; 不等式两边同乘一个负数, 所得不等式与原不等式反向.
利用这些基本性质, 我们还可以推导出其他一些常用的不等式的性质. 例如, 利用性质 2,3 可以推出:
性质 5
如果 , 那么 .
证明
事实上, 由 和性质 3 , 得 ; 由 和性质 3 , 得 . 再根据性质 2 , 即得 .
利用性质 4 和性质 2 可以推出:
性质 6
如果 , 那么 .
性质 7
如果 , 那么 .
实数大小关系的基本事实和不等式的性质是解决不等式问题的基本依据.
例 2
已知 , 求证 .
分析:
要证明 , 因为 , 所以可以先证明 . 利用已知 和性质 4 ,即可证明 .
证明:
因为 , 所以 .
于是
即
由 , 得 .
练习
1.
证明不等式性质 .
2.
用不等号 “ ” 或 “ ” 填空:
(1) 如果 , 那么 _ _ _ ;
(2) 如果 , 那么 _ _ _ ;
(3) 如果 , 那么 _ _ _ ;
(4) 如果 , 那么 _ _ _ .
习题 2.1
复习巩固
1.
举出几个现实生活中与不等式有关的例子.
2.
某市环保局为增加城市的绿地面积, 提出两个投资方案: 方案 A 为一次性投资 500 万元; 方案 为第一年投资 100 万元, 以后每年投资 10 万元. 列出不等式表示 “经过 年之后, 方案 的投入不少于方案 的投入”.
3.
比较下列各组中两个代数式的大小:
(1) 与 ;
(2) 与 ;
(3) 当 时, 与 ;
(4) 与 .
4.
一个大于 50 且小于 60 的两位数, 其个位数字比十位数字大 2 . 试用不等式表示上述关系, 并求出这个两位数 (用 和 分别表示这个两位数的十位数字和个位数字).
5.
已知 , 求 的取值范围.
6.
证明: .
综合运用
7.
已知 , 求证 .
8.
下列命题为真命题的是 ( ).
(A) 若 , 则
(B) 若 , 则
© 若 , 则
(D) 若 , 则
9.
证明: 圆的面积大于与它具有相同周长的正方形的面积. 并据此说明, 人们通常把自来水管的横截面制成圆形,而不是正方形的原因.
10.
已知 克糖水中含有 克糖 , 再添加 克糖 (假设全部溶解 , 糖水变甜了. 请将这一事实表示为一个不等式, 并证明这个不等式成立.
拓广探索
11.
已知 , 求证 .
12.
火车站有某公司待运的甲种货物 , 乙种货物 . 现计划用 A, B两种型号的货厢共 50 节运送这批货物. 已知 甲种货物和 乙种货物可装满一节 型货厢, 甲种货物和 乙种货物可装满一节 型货厢, 据此安排 A, B 两种货厢的节数, 共有几种方案? 若每节 型货厢的运费是 0.5 万元, 每节 型货厢的运费是 0.8 万元, 哪种方案的运费较少?