6.1 平面向量的概念
2024-05-13 22:29:39 新建
我们知道, 力、位移、速度等物理量是既有大小、又有方向的量. 本节我们将通过对这些量的抽象, 形成向量概念及其表示方法; 通过研究向量之间的一些特殊关系, 初步认识向量的一些特征.
6.1.1 向量的实际背景与概念
例子
在本章引言中, 小船位移的大小是 两地之间的距离 mile, 位移的方向是东南方向; 小船航行速度的大小是 mile/h, 速度的方向是东南方向. 又如, 物体受到的重力是坚直向下的 (图 6.1-1), 物体的质量越大, 它受到的重力越大; 物体在液体中受到的浮力是坚直向上的 (图 6.1-2), 物体浸在液体中的体积越大, 它受到的浮力越大.
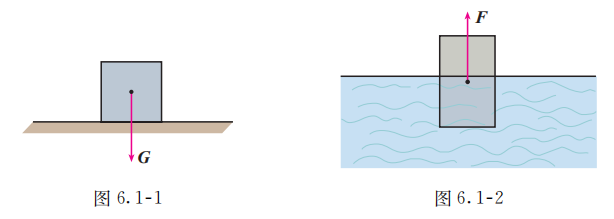
力、位移、速度等有各自的特性, 而 “既有大小, 又有方向” 是它们的共同属性. 我们知道, 从一支笔、一棵树、一本书 中, 可以抽象出只有大小的数量 “ 1 ”. 类似地, 我们可以对力、位移、速度 这些量进行抽象, 形成一种新的量.
定义 向量 数量
在数学中, 我们把既有大小又有方向的量叫做向量 (vector), 而把只有大小没有方向的量称为数量,
例子
如年龄、身高、长度、面积、体积、质量等都是数量.
思考
物理学中常称向量为矢量, 数量为标量, 你还能举出物理学中的一些向量和数量吗?
6.1.2 向量的几何表示
由于数量可以用实数表示, 而实数与数轴上的点一一对应, 所以数量可用数轴上的点表示, 而且不同的点表示不同的数量. 那么, 该如何表示向量呢?
例子
我们仍以位移为例, 小船以 为起点, 为终点, 我们可以用连接 两点的线段长度代表小船行进的距离, 并在终点 处加上箭头表示小船行驶的方向. 于是, 这条 “带有方向的线段” 就可以用来表示位移. 受此启发, 我们可以用带箭头的线段来表示向量,线段按一定比例 (标度) 画出, 它的长短表示向量的大小, 箭头的指向表示向量的方向.
定义 有向线段
通常, 在线段 的两个端点中, 规定一个顺序, 假设 为起点, 为终点, 我们就说线段 具有方向, 具有方向的线段叫做有向线段(directed line segment) (图 6.1-3).通常在有向线段的终点处画上箭头表示它的方向. 以 为起点、 为终点的有向线段记作 , 线段 的长度也叫做有向线段 的长度, 记作 .
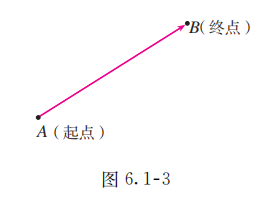
表示有向线段时,起点一定要写在终点的前面.
有向线段包含三个要素: 起点、方向、长度. 知道了有向线段的起点、方向和长度, 它的终点就唯一确定了.
向量可以用有向线段 来表示, 我们把这个向量记作向量 . 有向线段的长度 表示向量的大小, 有向线段的方向表示向量的方向. 用有向线段表示向量, 使向量有了直观形象.
定义 向量
向量 的大小称为向量 的长度 (或称模), 记作 . 长度为 0 的向量叫做零向量 (zero vector), 记作 .长度等于 1 个单位长度的向量, 叫做单位向量 (unit vector).
向量也可以用字母 表示.
印刷用黑体 , 书写用 .
例 1
在图 6.1-4 中, 分别用向量表示 地至 两地的位移, 并根据图中的比例尺, 求出 地至 两地的实际距离(精确到 ).
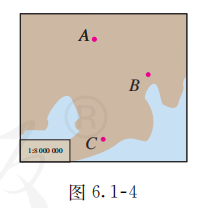
解:
表示 地至 地的位移,且 ;
表示 地至 地的位移, 且 .
6.1.3 相等向量与共线向量
下面, 我们通过向量之间的关系进一步认识向量.
定义 平行向量
方向相同或相反的非零向量叫做平行向量 (parallel vectors). 如图 6.1-5, 用有向线段表示的向量 与 是两个平行向量.向量 与 平行, 记作 .
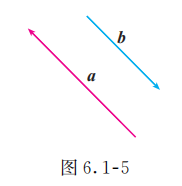
我们规定:零向量与任意向量平行, 即对于任意向量 , 都有 .
定义 相等向量
长度相等且方向相同的向量叫做相等向量 (equal vectors). 如图 6.1-6, 用有向线段表示的向量 与 相等, 记作 .
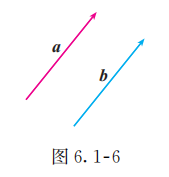
定理
任意两个相等的非零向量, 都可用同一条有向线段表示, 并且与有向线段的起点无关; 同时, 两条方向相同且长度相等的有向线段表示同一个向量, 因为向量完全由它的模和方向确定.
定义 共线向量
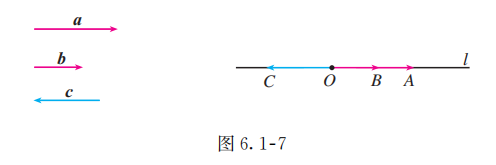
如图 6.1-7, 是一组平行向量, 任作一条与 所在直线平行的直线 , 在 上任取一点 , 则可在 上分别作出 . 这就是说, 任一组平行向量都可以平移到同一条直线上, 因此, 平行向量也叫做共线向量 (collinear vectors).
例 2
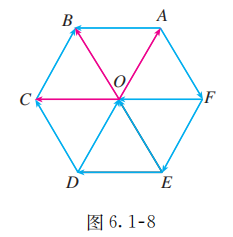
如图 6.1-8, 设 是正六边形 的中心.
(1) 写出图中的共线向量;
(2) 分别写出图中与 相等的向量.
解:
(1)
是共线向量;
是共线向量;
是共线向量.
(2)
;
;
.
练习
1.
下列量中哪些是向量?
悬挂物受到的拉力, 压强, 摩擦力, 频率, 加速度.
2.
画两条有向线段, 分别表示一个坚直向下、大小为 的力和一个水平向左、大小为 的力. (用 长表示 )
3.
指出图中各向量的长度. (规定小方格的边长为 0.5 )
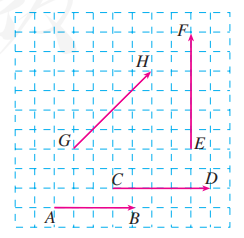
4.
将向量用具有同一起点 的有向线段表示.
(1) 当 与 是相等向量时, 判断终点 与 的位置关系;
(2) 当 与 是平行向量, 且 时, 求向量 的长度, 并判断 的方向与 的方向之间的关系.
习题 6.1
复习巩固
1.
在如图所示的坐标纸 (规定小方格的边长为 1) 中, 用直尺和圆规画出下列向量:
(1) , 点 在点 正南方向;
(2) , 点 在点 北偏西 方向;
(3) , 点 在点 南偏西 方向.

2.
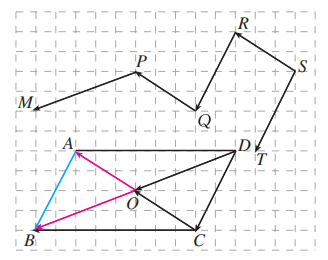
如图, 点 是平行四边形 的对角线的交点, 且 , 分别写出 和折线 MPQRST 中与 相等的向量.
综合运用
3.
判断下列结论是否正确(正确的在括号内打 “ ”, 错误的打 “ ”), 并说明理由.
(1) 若 与 都是单位向量, 则 .
(2) 方向为南偏西 的向量与北偏东 的向量是共线向量.
(3) 直角坐标平面上的 轴、 轴都是向量.
(4) 若 与 是平行向量, 则 .
(5) 若用有向线段表示的向量 与 不相等, 则点 与 不重合.
(6) 海拔、温度、角度都不是向量.
拓广探索
4.
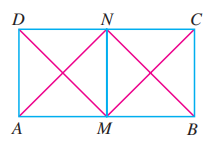
如图, 在矩形 中, 分别为边 , 的中点, 在以 为起点和终点的所有有向线段表示的向量中, 相等的向量共有多少对?
阅读与思考
向量及向量符号的由来
向量最初应用于物理学, 被称为矢量. 很多物理量, 如力、位移、速度、电场强度、磁感应强度等都是向量. 向量的概念萌芽于两千多年前, 大约在公元前 350 年, 古希腊著名学者亚里士多德 (Aristotle, 公元前 384 - 前 322) 就知道了力可以表示成向量. “向量”一词来自力学、解析几何中的有向线段. 最先使用有向线段表示向量的是英国科学家牛顿(Isaac Newton,1642-1727).
向量是一种带几何性质的量, 除零向量外, 总可以画出 “箭头表示方向, 线段长表示大小” 的有向线段来表示它. 1806 年, 瑞士人阿尔冈 (J. R. Argand, 1768-1822) 以 表示有向线段或向量. 1827 年, 默比鸟斯(A. F. Möbius, 1790-1868) 以 表示起点为 , 终点为 的向量, 这种用法被数学家广泛接受. 另外, 哈密顿 (W. R. Hamilton, 1805-1865) 、吉布斯 (J. W. Gibbs, 1839-1903)等人则以小写希腊字母表示向量. 后来, 字母上加箭头表示向量的方法逐渐流行, 尤其用在手写稿中; 为了方便印刷, 人们又用粗黑体小写字母 , 等表示向量. 这两种符号一直沿用至今.
莱布尼茨 (G. W. Leibniz, 1646-1716) 曾经从位置几何学研究的视角进行过预想: “我已经发现了一些完全不同的有新特点的元素, 即使在没有任何图形的情况下, 它也能有利于表达思想、表达事物的本质. 我的这个新系统能紧跟可见的图形, 以一种自然的、分析的方式, 通过一个确定的程序同时给出解、构造和几何的证明.” 莱布尼茨所说的 “有新特点的元素” 和 “新系统” 就是逐渐形成和发展起来的向量及其理论.
向量进入数学并得到发展, 是从复数的几何表示开始的. 1797 年, 丹麦测量学家韦塞尔 (Caspar Wessel, 1745-1818) 把复数表示为向量, 并利用向量定义复数运算. 他把坐标平面上的点用向量表示出来, 并把向量的几何表示用于研究几何与三角问题. 人们逐步接受了复数, 也学会了利用复数表示、研究平面中的向量.
发展到现在, 向量在数学、物理、计算机科学与技术等学科, 以及社会生产、生活、经济、金融与贸易等各领域中都有广泛的应用, 成为解决这些学科或领域中各种问题的有力工具.
思考
你能说一说用符号表示向量所起的重要作用吗?