5.8 小结
2024-05-11 22:34:30 新建
本章知识结构

回顾与思考
现实世界中存在着大量周期现象, 任意角的三角函数就是刻画这种现象的基本而有效的数学模型.
为了建立三角函数概念, 本章我们先把角的范围推广到任意角, 并引进弧度制; 然后借助单位圆建立了一般三角函数的概念. 接着, 利用单位圆的性质 (主要是对称性), 用几何直观和代数运算的方法研究了三角函数的周期性、对称性、单调性和最大(小)值等性质.和(差)角公式、倍角公式等反映了三角函数之间的内在联系, 也是圆的几何性质的代数表示, 我们借助单位圆, 通过代数运算对这些关系进行了研究. 最后, 利用三角函数的概念和性质, 建立了具有广泛应用价值的函数 , 并用它解决了许多实际问题.
根据第三章给出的概念, 函数是两个实数集之间的对应. 这样, 我们不仅可以对各种函数进行加、减、乘、除等运算, 还可以在自变量与函数值之间进行运算, 从而使函数具有更广泛的应用. 弧度制的本质是用长度单位来度量角的大小, 统一了三角函数自变量和函数值的单位, 从而使三角函数成为从实数集到实数集之间的对应. 如果只用角度制, 那么将导致自变量是 60 进位的角度、函数值是 10 进位的实数, 例如 之类的运算将失去意义. 所以, 弧度制的引入对建立任意角的三角函数概念是至关重要的. 在本章中已经看到, 三角函数可以刻画振动、波动等大量周期现象, 它们的自变量不是角度, 而是时间、距离等其他量, 这也说明了引入弧度制的必要性. 在今后的学习中, 我们还会不断体验到引入弧度制对拓展三角函数应用范围的必要性.
将角放在直角坐标系中讨论不但使角的表示有了统一的方法, 而且使我们能够借助直角坐标系中的单位圆, 建立角的变化与单位圆上点的变化之间的对应关系,从而建立正弦函数、余弦函数. 因此, 正弦函数、余弦函数的性质与圆的几何性质(主要是对称性)之间存在着非常紧密的联系. 例如, 和单位圆相关的 “勾股定理”与同角三角函数的基本关系有内在的一致性; 单位圆周长为 与正弦函数、余弦函数的周期为 是一致的; 圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的; 等等. 因此, 在研究三角函数时, 单位圆的作用非常重要.
周期性是三角函数最重要的性质, 利用周期性, 我们只要研究清楚三角函数在一个最小正周期内的性质即可; 除了奇偶性外, 三角函数还有非常丰富的对称性, 诱导公式就是三角函数对称性的体现. 利用周期性、奇偶性和诱导公式等可以发现, 轴上的点 都是正弦函数 的对称中心,而直线 则都是正弦函数 的对称轴. 对于余弦函数、正切函数可以得到类似的结论.
本章出现了大量三角公式, 这些公式具有紧密的联系. 其中, 和(差)角公式具有一般意义, 诱导公式、倍角公式等都可以看作它的特例. 学习时要充分利用这种联系性, 避免对公式的死记硬背.
三角函数是一类特殊的周期函数, 在研究三角函数时, 既可以联系物理、生物、自然界中的周期现象(运动), 也可以从已学过的指数函数、对数函数、幂函数等得到启发, 还要注意与锐角三角函数建立联系. 这种关系可以用以下框图表示:

请你带着下面的问题, 复习一下全章内容吧!
- 从本章的学习中可以看到, 弧度制的引入为三角函数的研究奠定了基础.你能概括一下引入弧度制的必要性吗?
- 回顾三角函数的定义方法, 说说它与幂函数、指数函数的定义方法的共性和差异性.
- 单位圆在三角函数的研究中有非常重要的作用. 你能借助单位圆, 自己归纳一下研究三角函数的图象与性质的过程与方法吗?
- 两角差的余弦公式 不仅是和(差)角公式的基础, 也可以看成诱导公式的一般化. 你能画一张本章公式的 “逻辑图” 吗? 推导这些公式的过程中用到了哪些数学思想方法?
- 函数 在刻画周期现象时有着非常重要的作用, 其中参数 都有相应的实际意义. 你能借助匀速圆周运动或其他周期现象(如简谐振动、单摆等), 说明这些参数的意义, 以及它们的变化对函数图象的影响吗?
- 你能针对现实生活中的某种周期现象, 用适当的方法搜集数据, 并利用这些数据为这种周期现象建立一个函数模型吗?
复习参考题 5
复习巩固
1.
写出与下列各角终边相同的角的集合 , 并且把 中适合不等式 的元素 写出来:
(1) ;
(2) ;
(3) ;
(4) 0 .
2.
一个扇形的弧长与面积的数值都是 5 , 求这个扇形中心角的度数(精确到 ).
3.
(1) 已知 , 求 .
(2) 已知 , 求角 的三个三角函数值.
4.
已知 , 计算:
(1)
(2) ;
(3) ;
(4) .
5.
计算 (可用计算工具, 第 (2) (3)题精确到 0.0001 ):
(1) ;
(2) ;
(3) .
6.
设 , 填表:
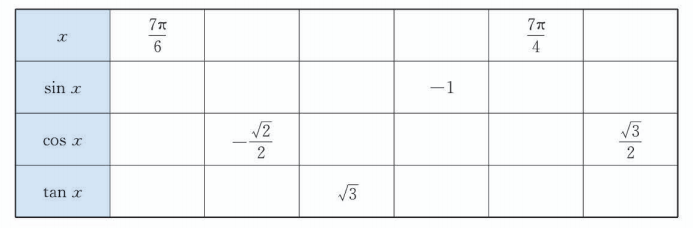
7.
求下列函数的最大值、最小值, 并求使函数取得最大、最小值的 的集合:
(1) ;
(2) .
8.
画出下列函数在长度为一个周期的闭区间上的简图, 并指出分别由函数 的图象经过怎样的变换得到:
(1) ;
(2) ;
(3) ;
(4) .
9.
(1) 用描点法画出函数 的图象.
(2) 如何根据第 (1) 小题并运用正弦函数的性质, 得到函数 的图象?
(3) 如何根据第 (2) 小题并通过平行移动坐标轴, 得到函数 都是常数) 的图象?
10.
不通过画图, 写出下列函数的振幅、周期、初相, 并说明如何由正弦曲线得到它们的图像:
(1) ;
(2) .
11.
(1) 已知 都是锐角, , 求 的值;
(2) 已知 , 求 的值;
(3) 已知 都是锐角, , 求 的值.
12.
(1) 证明 ;
(2) 求 的值;
(3) 若 , 求 的值;
(4) 求 的值.
13.
化简:
(1) ;
(2) ;
(3) ;
(4) .
14.
(1) 已知 , 求 的值;
(2) 已知 , 求 的值;
(3) 已知 , 求 的值;
(4) 已知 , 求 的值.
15.
(1) 已知 , 求 的值;
(2) 已知 , 求 的值.
综合运用
16.
证明:
(1) ;
(2) ;
(3) ;
(4) .
17.
已知 , 求 的值.
18.
已知 , 求 的值.
19.
已知 , 求证 .
20.
已知函数 ,
(1) 求 的最小正周期;
(2) 当 时, 求 的最小值以及取得最小值时 的集合.
21.
已知函数 的最大值为 1 ,
(1) 求常数 的值;
(2) 求函数 的单调递减区间;
(3) 求使 成立的 的取值集合.
22.
已知函数 在区间 上的最大值为 6 ,
(1) 求常数 的值;
(2) 当 时, 求函数 的最小值, 以及相应 的集合.
23.
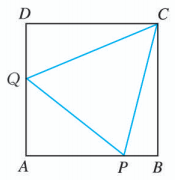
如图, 正方形 的边长为 分别为边 上的点.当 的周长为 2 时, 求 的大小.
拓广探索
24.
已知 ,
(1) 求 的值;
(2) 你能根据所给的条件,自己构造出一些求值问题吗?
25.
如图, 已知直线 是 之间的一定点, 并且点 到 的距离分别为 . 是直线 上一动点, 作 , 且使 与直线 交于点 . 设 .

(1) 写出 的面积 关于角 的函数解析式 ;
(2) 画出上述函数的图象;
(3) 由 (2) 中的图象求 的最小值.
26.
英国数学家泰勒给出如下公式:
,
其中 .
这些公式被编人计算工具, 计算工具计算足够多的项就可以确保显示值的精确性. 比如, 用前三项计算 , 就得到 .
试用你的计算工具计算 , 并与上述结果比较.
27.
在地球公转过程中, 太阳直射点的纬度随时间周而复始不断变化.
(1) 如图, 设地球表面某地正午太阳高度角为 为此时太阳直射点的纬度, 为当地的纬度值, 那么这三个量满足 .
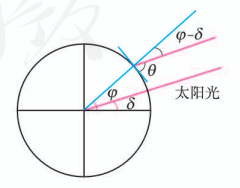
某科技小组以某年春分(太阳直射赤道且随后太阳直射点逐渐北移的时间)为初始时间, 统计了连续 400 天太阳直射点的纬度平均值(太阳直射北半球时取正值, 太阳直射南半球时取负值). 下面是该科技小组的三处观测站成员在春分后第 45 天测得的当地太阳高度角数据:
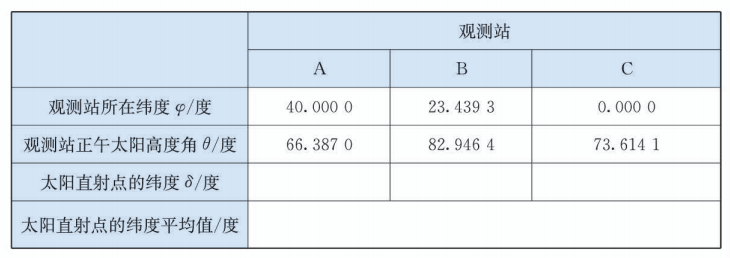
请根据数据完成上面的表格(计算结果精确到 0.0001 );
(2) 设第 天时太阳直射点的纬度平均值为 . 该科技小组通过对数据的整理和分析, 推断 与 近似满足函数 , 其中 为北回归线的纬度值, 约为 23.4392911 , 试利用 (1) 中的数据, 估计 的值(精确到 );
(3) 定义从某年春分到次年春分所经历的时间为一个回归年, 求一个回归年对应的天数(精确到 0.0001;
(4) 利用 (3) 的结果, 估计每 400 年中, 应设定多少个闰年, 可使这 400 年与 400 个回归年所含的天数最为接近(精确到 1 ).