5.7 三角函数的应用

2024-05-07 22:30:53 新建

现实生活中存在大量具有周而复始、循环往复特点的周期运动变化现象, 如果某种变化着的现象具有周期性, 那么就可以考虑借助三角函数来措述. 本节通过几个具体实例,说明三角函数模型的简单应用.

问题 1

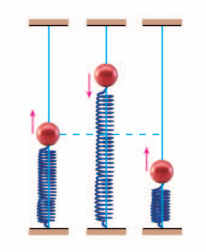
某个弹簧振子 (简称振子) 在完成一次全振动的过程中, 时间 $t$ (单位: s) 与位移 $y$ (单位: $mm$ ) 之间的对应数据如表 5.7-1 所示. 试根据这些数据确定这个振子的位移关于时间的函数解析式.

答

振子的振动具有循环往复的特点, 由振子振动的物理学原理可知, 其位移 $y$ 随时间 $t$ 的变化规律可以用函数 $y =$ $A sin (ω t + φ)$ 来刻画.

根据已知数据作出散点图, 如图 5.7-1 所示.

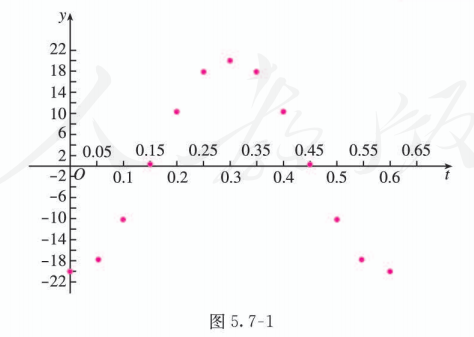
由数据表和散点图可知, 振子振动时位移的最大值为 $20 mm$ , 因此 $A = 20$ ; 振子振动的周期为 $0.6 s$ , 即 $\frac{2 π}{ω} = 0.6$ , 解得 $ω = \frac{10 π}{3}$ ; 再由初始状态 $(t = 0)$ 振子的位移为 $- 20$ , 可得 $sin φ = - 1$ , 因此 $φ = - \frac{π}{2}$ . 所以振子位移关于时间的函数解析式为

$y = 20 sin (\frac{10 π}{3} t - \frac{π}{2}), t \in [0, + \infty) .$

探究

请你查阅资料, 了解振子的运动原理.

定义简谐运动振幅、周期、频率、相位、初相

现实生活中存在大量类似弹簧振子的运动, 如钟摆的摆动, 水中浮标的上下浮动, 琴弦的振动, 等等. 这些都是物体在某一中心位置附近循环往复的运动. 在物理学中, 把物体受到的力（总是指向平衡位置）正比于它离开平衡位置的距离的运动称为 “简谐运动”.可以证明, 在适当的直角坐标系下, 简谐运动可以用函数 $y = A sin (ω x + φ), x \in [0, + \infty)$ 表示, 其中 $A > 0, ω > 0$ . 描述简谐运动的物理量, 如振幅、周期和频率等都与这个解析式中的常数有关:

$A$ 就是这个简谐运动的振幅, 它是做简谐运动的物体离开平衡位置的最大距离;
这个简谐运动的周期是 $T = \frac{2 π}{ω}$ , 它是做简谐运动的物体往复运动一次所需要的时间;
这个简谐运动的频率由公式 $f = \frac{1}{T} = \frac{ω}{2 π}$ 给出, 它是做简谐运动的物体在单位时间内往复运动的次数;
$ω x + φ$ 称为相位; $x = 0$ 时的相位 $φ$ 称为初相.

问题 2

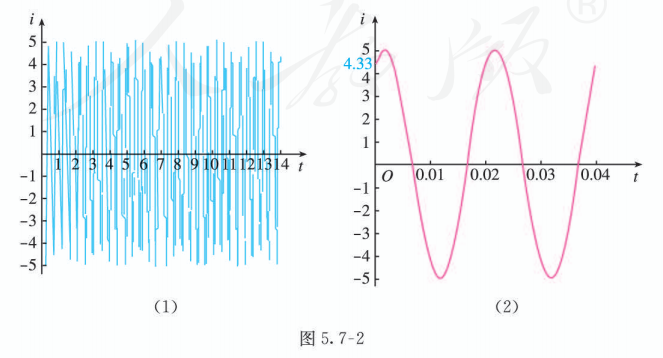
图 5.7-2(1) 是某次实验测得的交变电流 $i$ (单位: A) 随时间 $t$ (单位: s) 变化的图象. 将测得的图象放大，得到图 5.7-2(2).
(1) 求电流 $i$ 随时间 $t$ 变化的函数解析式;
(2) 当 $t = 0, \frac{1}{600}, \frac{1}{150}, \frac{7}{600}, \frac{1}{60}$ 时, 求电流 $i$ .

答

由交变电流的产生原理可知, 电流 $i$ 随时间 $t$ 的变化规律可用 $i = A sin (ω t + φ)$ 来刻画, 其中 $\frac{ω}{2 π}$ 表示频率, $A$ 表示振幅, $φ$ 表示初相.

由图 5.7-2(2) 可知, 电流最大值为 $5 A$ , 因此 $A = 5$ ; 电流变化的周期为 $\frac{1}{50} s$ , 频率为 $50 Hz$ , 即 $\frac{ω}{2 π} = 50$ , 解得 $ω = 100 π$ ; 再由初始状态 $(t = 0)$ 的电流约为 $4.33 A$ , 可得 $sin φ = 0.866$ , 因此 $φ$ 约为 $\frac{π}{3}$ . 所以电流 $i$ 随时间 $t$ 变化的函数解析式是

$i = 5 sin (100 π t + \frac{π}{3}), t \in [0, + \infty) .$

当 $t = 0$ 时, $i = \frac{5 3}{2}$ ;
当 $t = \frac{1}{600}$ 时, $i = 5$ ;
当 $t = \frac{1}{150}$ 时, $i = 0$ ;
当 $t = \frac{7}{600}$ 时, $i = - 5$ ;
当 $t = \frac{1}{60}$ 时, $i = 0$ .

探究

请你查阅资料, 了解交变电流的产生原理.

练习

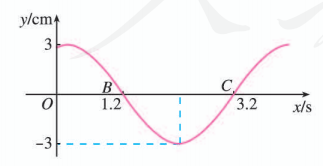
某简谐运动的图象如图所示, 试根据图像回答下列问题:
(1) 这个简谐运动的振幅、周期与频率各是多少?
(2) 写出这个简谐运动的函数解析式.

如图, 一根绝对刚性且长度不变、质量可忽略不计的线, 一端固定, 另一端悬挂一个沙漏. 让沙漏在偏离平衡位置一定角度 (最大偏角) 后在重力作用下在铅垂面内做周期摆动. 若线长为 $l cm$ , 沙漏摆动时离开平衡位置的位移 $s$ （单位: $cm$ ) 与时间 $t$ （单位: $s$ ）的函数关系是

$s = 3 cos (\frac{g}{l} t + \frac{π}{3}), t \in [0, + \infty) .$

(1) 当 $l = 25$ 时, 求该沙漏的最大偏角（精确到 $0.0001 rad ）;$
(2) 已知 $g = 9.8 m / s^{2}$ , 要使沙漏摆动的周期是 $1 s$ , 线的长度应当是多少（精确到 $0.1 cm$ )?

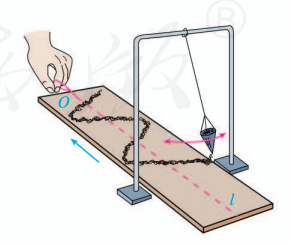
一台发电机产生的电流是正弦式电流，电压和时间之间的关系如图所示. 由图象说出它的周期、频率和电压的最大值, 并求出电压 $U$ (单位: V) 关于时间 $t$ (单位: s) 的函数解析式.

建模思想

匀速圆周运动、简谐运动和交变电流都是理想化的运动变化现象, 可以用三角函数模型准确地描述它们的运动变化规律. 在现实生活中也有大量运动变化现象, 仅在一定范围内呈现出近似于周期变化的特点, 这些现象也可以借助三角函数近似地描述.

例 1

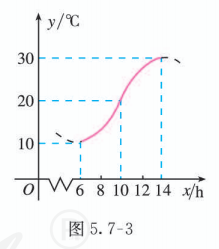
如图 5.7-3, 某地一天从 $6 \sim 14$ 时的温度变化曲线近似满足函数

$y = A sin (ω x + φ) + b .$

(1) 求这一天 $6 \sim 14$ 时的最大温差;
(2) 写出这段曲线的函数解析式.

解：

(1) 由图 5.7-3 可知, 这段时间的最大温差是 $2 0^{\circ} C$ .
(2) 由图 5.7-3 可以看出, 从 $6 \sim 14$ 时的图象是函数

$y = A sin (ω x + φ) + b (\overset{◯}{1})$

的半个周期的图象，所以

$A = \frac{1}{2} (30 - 10) = 10, b = \frac{1}{2} (30 + 10) = 20.$

因为 $\frac{1}{2} \times \frac{2 π}{ω} = 14 - 6$ , 所以 $ω = \frac{π}{8}$ .
将 $A = 10, b = 20, ω = \frac{π}{8}, x = 6, y = 10$ 代人 $\overset{◯}{1}$ 式, 可得 $φ = \frac{3 π}{4}$ .
综上, 所求解析式为

$y = 10 sin (\frac{π}{8} x + \frac{3 π}{4}) + 20, x \in [6, 14] .$

建模思想

一般地, 所求出的函数模型只能近似刻画这天某个时段的温度变化情况, 因此应当特别注意自变量的变化范围.

例 2

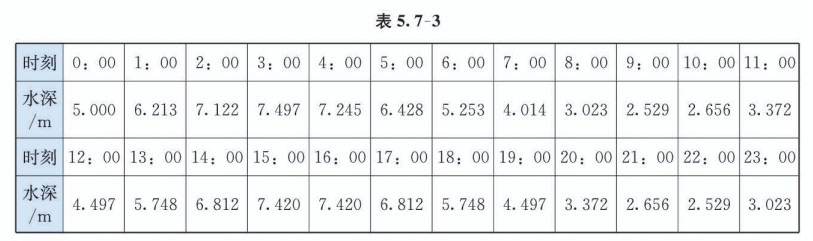
海水受日月的引力, 在一定的时候发生涨落的现象叫潮. 一般地, 早潮叫潮,晚潮叫汐. 在通常情况下, 船在涨潮时驶进航道, 靠近码头; 卸货后, 在落潮时返回海洋. 表 5.7-2 是某港口某天的时刻与水深关系的预报.

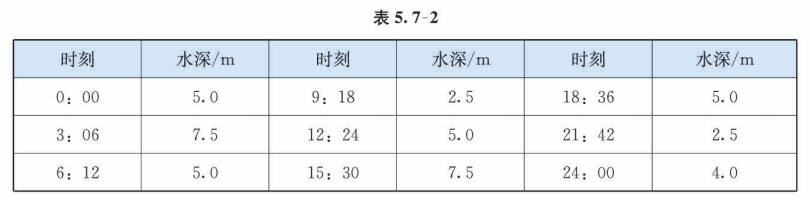
(1) 选用一个函数来近似描述这一天该港口的水深与时间的关系, 给出整点时水深的近似数值（精确到 $0.001 m$ ).
(2) 一条货船的吃水深度 (船底与水面的距离) 为 $4 m$ , 安全条例规定至少要有 $1.5 m$ 的安全间隙（船底与洋底的距离）, 该船这一天何时能进入港口? 在港口能待多久?
(3) 某船的吃水深度为 $4 m$ , 安全间隙为 $1.5 m$ , 该船这一天在 $2 : 00$ 开始卸货, 吃水深度以 $0.3 m / h$ 的速度减少. 如果这条船一直卸货, 那么港口水深将在某一时刻与这条船需要的安全水深相等. 为了安全, 这条船需要在这一时刻前至少 $0.4 h$ 停止卸货并驶离港口, 那么该船最好在什么时间停止卸货并驶离港口?

分析:

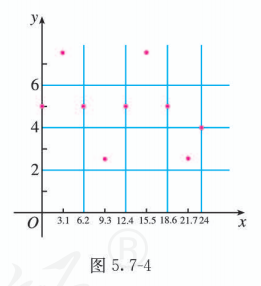
观察问题中所给出的数据, 可以看出, 水深的变化具有周期性. 根据表 5.7-2 中的数据画出散点图, 如图 5.7-4. 从散点图的形状可以判断, 这个港口的水深与时间的关系可以用形如 $y = A sin (ω x + φ) + h$ 的函数来刻画, 其中 $x$ 是时间, $y$ 是水深. 根据数据可以确定 $A, ω, φ, h$ 的值.

解：

(1) 以时间 $x$ (单位: h) 为横坐标, 水深 $y$ (单位: m) 为纵坐标, 在直角坐标系中画出散点图 (图 5.7-4).根据图象, 可以考虑用函数 $y = A sin (ω x + φ) + h$ 刻画水深与时间之间的对应关系. 从数据和图象可以得出:

$A = 2.5, h = 5, T = 12.4, φ = 0;$

由 $T = \frac{2 π}{ω} = 12.4$ , 得

$ω = \frac{5 π}{31} .$

所以, 这个港口的水深与时间的关系可用函数 $y = 2.5 sin \frac{5 π}{31} x + 5$ 近似描述.

由上述关系式易得港口在整点时水深的近似值（表 5.7-3）:

(2) 货船需要的安全水深为 $4 + 1.5 = 5.5 m$ , 所以当 $y ⩾ 5.5$ 时就可以进港. 令

$2.5 sin \frac{5 π}{31} x + 5 = 5.5, sin \frac{5 π}{31} x = 0.2.$

由计算器可得

$0.2013579208 \approx 0.2014$ .

// 科学计算器上, 有 $sin^{- 1} 、 cos^{- 1} 、 tan^{- 1}$ 三个键, 在已知一个三角函数值时, 可以利用它们求出对应的角.

如图 5.7-5, 在区间 $[0, 12]$ 内, 函数 $y = 2.5 sin \frac{5 π}{31} x + 5$ 的图象与直线 $y = 5.5$ 有两个交点 $A, B$ , 因此

$\frac{5 π}{31} x \approx 0.2014, 或 π - \frac{5 π}{31} x \approx 0.2014.$

解得

$x_{A} \approx 0.3975, x_{B} \approx 5.8025$

由函数的周期性易得：

$x_{C} \approx 12.4 + 0.3975 = 12.7975, x_{D} \approx 12.4 + 5.8025 = 18.2025.$

因此, 货船可以在零时 30 分左右进港, 5 时 45 分左右出港; 或在 13 时左右进港, 18 时左右出港. 每次可以在港口停留 5 小时左右.

(3) 设在 $x h$ 时货船的安全水深为 $y m$ , 那么 $y = 5.5 - 0.3 (x - 2) (x ⩾ 2)$ . 在同一直角坐标系内画出这两个函数的图象, 可以看到在 $6 \sim 8$ 时之间两个函数图象有一个交点 (图 5.7-6).

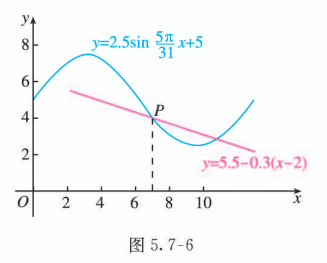
借助计算工具, 用二分法可以求得点 $P$ 的坐标约为 $(7.016, 3.995)$ , 因此为了安全, 货船最好在 6.6 时之前停止卸货并驶离港口.

建模思想

三角函数作为描述现实世界中周期现象的一种数学模型, 可以用来研究很多问题, 在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.

具体地, 我们可以利用搜集到的数据, 先画出相应的 “散点图”、观察散点图, 然后进行函数拟合获得具体的函数模型, 最后利用这个函数模型来解决相应的实际问题.

实际问题通常涉及复杂的数据, 因此往往需要使用信息技术.

练习

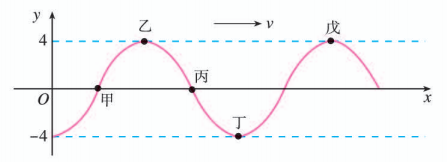
下图为一向右传播的绳波在某一时刻绳子各点的位置图, 经过 $\frac{1}{2}$ 周期后, 乙点的位置将移至何处?

自出生之日起, 人的体力、情绪、智力等心理、生理状况就呈周期变化. 根据心理学家的统计, 人体节律分为体力节律、情绪节律和智力节律三种. 这些节律的时间周期分别为 23 天、 28 天、 33 天.每个节律周期又分为高潮期、临界日和低潮期三个阶段. 以上三个节律周期的半数为临界日, 这就是说 11.5 天、 14 天、 16.5 天分别为体力节律、情绪节律和智力节律的临界日. 临界日的前半期为高潮期, 后半期为低潮期. 生日前一天是起始位置 (平衡位置), 请根据自己的出生日期, 绘制自己的体力、情绪和智力曲线, 并总结自己在什么时候应当控制情绪, 在什么时候应当鼓励自己; 在什么时候应当加强锻炼, 在什么时候应当保持体力.

习题 5.7

综合运用

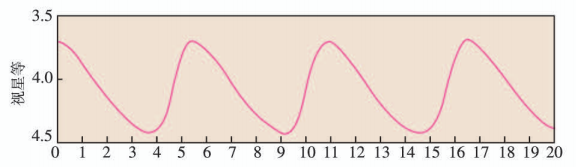
天上有些恒星的亮度是会变化的, 其中一种称为造父 (型) 变星, 本身体积会膨胀收缩造成亮度周期性的变化. 下图是一造父变星的亮度随时间的周期变化图. 此变星的亮度变化的周期为多少天? 最亮时是几等星? 最暗时是几等星?

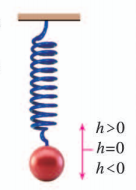
如图, 弹簧挂着的小球做上下运动, 它在 $t s$ 时相对于平衡位置的高度 $h$ (单位: $cm)$ 由关系式 $h = 2 sin (t + \frac{π}{4})$ 确定. 以 $t$ 为横坐标, $h$ 为纵坐标, 画出这个函数在一个周期的闭区间上的图象, 并回答下列问题:
(1) 小球在开始振动（即 $t = 0$ ) 时的位置在哪里?
(2) 小球的最高点和最低点与平衡位置的距离分别是多少?
(3) 经过多少时间小球往复运动一次?
(4) 每秒钟小球能往复振动多少次?

拓广探索

北京天安门广场的国旗每天是在日出时随太阳升起, 在日落时降旗. 请根据年鉴或其他参考资料, 统计过去一年不同日期的日出和日落时间.
(1) 在同一直角坐标系中, 以日期为横轴, 画出散点图, 并用曲线去拟合这些数据, 同时找到函数模型;
(2) 某同学准备在五一长假时去看升旗, 他应当在几点前到达天安门广场?

夏天是用电的高峰时期, 特别是在晚上, 为保证居民空调制冷用电, 电力部门不得不对企事业单位拉闸限电, 而到了零时以后, 又出现电力过剩的情况. 因此每天的用电也出现周期性的变化. 为保证居民用电, 电力部门提出了 “消峰平谷” 的想法, 即提高晚上高峰时期的电价, 同时降低后半夜低峰时期的电价, 鼓励各单位在低峰时用电. 请调查你们地区每天的用电情况,制定一项“消峰平谷” 的电价方案.

阅读与思考

振幅、周期、频率、相位

人体就是一个包含各种周期运动的生物体, 医学上把周期为 24 小时的生理运动称为中周期运动, 如血压、血糖浓度的变化; 小于 24 小时的叫短周期运动,如心跳、脉搏每分 $50 \sim 70$ 次、呼吸每分 $16 \sim 24$ 次; 大于 24 小时的叫长周期运动, 如人的情绪、体力、智力等.

声音中也包含着正弦函数, 声音是由于物体的振动产生的能引起听觉的波. 每一个音都是由纯音合成的, 纯音的数学模型是函数 $y = A sin ω t$ . 音有四要素:音调、响度、音长和音色. 这都与正弦函数的参数有关. 响度与振幅有关, 即与声波的能量有关, 振幅越大, 响度越大. 音长也与振幅有关, 声音消失过程是由于声波在传播过程中受阻尼振动, 系统的机械能随时间逐渐减小, 振动的振幅也逐渐减小. 音调与声波的振动频率是有关的, 频率低的声音低沉, 频率高的声音尖利. 像我们平时听到的乐音不只是一个音在响, 而是许多个音的结合, 称为复合音.复合音的产生是因为发声体在全段振动, 产生频率为 $f$ 的基音的同时, 其各部分,如二分之一、三分之一、四分之一部分也在振动, 产生的频率恰好是全段振动频率的倍数, 如 $2 f, 3 f, 4 f$ 等. 这些音叫谐音, 因为其振幅较小, 我们一般不易单独听出来. 所以我们听到的声音的函数是 $y = sin x + \frac{1}{2} sin 2 x + \frac{1}{3} sin 3 x + \frac{1}{4} sin 4 x + \dots$ .

音色一般是由基音和谐音的综合作用所决定的, 不同乐器、不同人发出的音调可以相同, 但音色不同, 人们由此分辨出不同的声音.

周期函数产生了美妙的音乐！