8.1 基本立体图形
2024-06-29 22:21:37 新建
在我们周围存在着各种各样的物体, 它们都占据着空间的一部分. 如果只考虑这些物体的形状和大小, 而不考虑其他因素, 那么由这些物体抽象出来的空间图形就叫做空间几何体. 本节我们主要从几何体的组成元素及其相互关系的角度, 认识几种最基本的空间几何体.
观察
如图 8.1-1, 这些图片中的物体具有怎样的形状? 在日常生活中, 我们把这些物体的形状叫做什么? 如何描述它们的形状?

观察一个物体, 将它抽象成空间几何体, 并描述它的结构特征, 应先从整体入手, 想象围成物体的每个面的形状、面与面之间的关系,并注意利用平面图形的知识.
在图 8.1-1 中, 可以发现纸箱、金字塔、茶叶盒、金刚石、储物箱等物体有相同的特点: 围成它们的每个面都是平面图形, 并且都是平面多边形; 纸杯、腰鼓、奶粉罐、篮球和足球、铅锤等物体也有相同的特点:围成它们的面不全是平面图形,有些面是曲面.
定义
一般地, 由若干个平面多边形围成的几何体叫做多面体 (polyhedron)(图 8.1-2). 围成多面体的各个多边形叫做多面体的面, 如面 , 面 ; 两个面的公共边叫做多面体的棱, 如棱 , 棱 ; 棱与棱的公共点叫做多面体的顶点, 如顶点 , 顶点 .
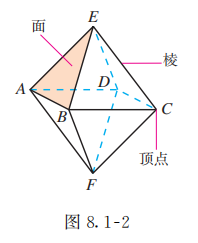
在空间几何体中说某个面是多边形, 一般也包括这个多边形内部的平面部分.
例子
图 8.1-1 中的纸箱、金字塔、茶叶盒、储物箱等物体都具有多面体的形状.
定义
一条平面曲线(包括直线)绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面, 封闭的旋转面围成的几何体叫做旋转体 (solid of rotation). 这条定直线叫做旋转体的轴. 图 8.1-3 中的旋转体就是由平面曲线 绕轴 旋转形成的.
例子
图 8.1-1 中的纸杯、奶粉罐、篮球和足球、铅锤等物体都具有旋转体的形状.
下面, 我们从多面体和旋转体组成元素的形状、位置关系入手, 进一步认识一些特殊的多面体和旋转体.
1. 棱柱
观察
观察图 8.1-4 中的长方体, 它的每个面是什么样的多边形? 不同的面之间有什么位置关系?
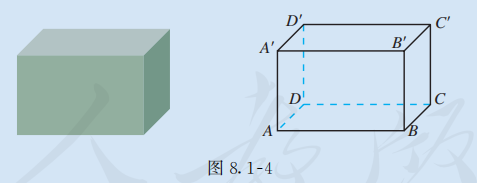
可以发现, 长方体的每个面都是平行四边形 (矩形), 并且相对的两个面, 如面 和面 , 给我们以平行的形象, 如同教室的地面和天花板一样.
定义
如图 8.1-5, 一般地, 有两个面互相平行, 其余各面都是四边形, 并且相邻两个四边形的公共边都互相平行, 由这些面所围成的多面体叫做棱柱 (prism). 图 8.1-1 中的茶叶盒所表示的多面体就是棱柱. 在棱柱中, 两个互相平行的面叫做棱柱的底面, 它们是全等的多边形; 其余各面叫做棱柱的侧面, 它们都是平行四边形; 相邻侧面的公共边叫做棱柱的侧棱; 侧面与底面的公共顶点叫做棱柱的顶点.
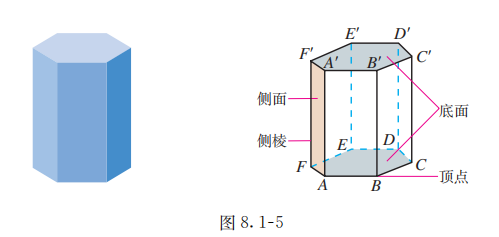
棱柱用表示底面各顶点的字母来表示, 如图 8.1-5 中的棱柱记作棱柱 . 棱柱的底面可以是三角形、四边形、五边形 , 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱 .
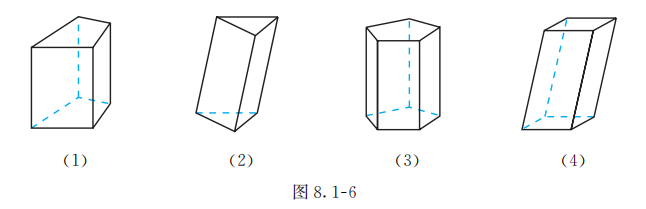
在图 8.1-4 中的长方体中, 侧棱和底面给我们以垂直的形象, 如同教室里相邻墙面的交线和地面的关系一样. 一般地, 我们把侧棱垂直于底面的棱柱叫做直棱柱(图 8.1-6(1) (3)), 侧棱不垂直于底面的棱柱叫做斜棱柱 (图 8.1-6(2)(4)). 底面是正多边形的直棱柱叫做正棱柱 (图 8.1-6(3)). 底面是平行四边形的四棱柱也叫做平行六面体 (图 8.1-6(4)).
2. 棱锥
像图 8.1-1 中金字塔这样的多面体, 均由平面图形围成, 其中一个面是多边形, 其余各面都是三角形, 并且这些三角形有一个公共顶点.
定义
如图 8.1-7, 一般地, 有一个面是多边形, 其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥 (pyramid). 这个多边形面叫做棱锥的底面; 有公共顶点的各个三角形面叫做棱锥的侧面; 相邻侧面的公共边叫做棱锥的侧棱; 各侧面的公共顶点叫做棱锥的顶点.
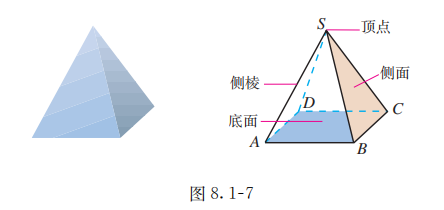
棱锥用表示顶点和底面各顶点的字母来表示, 如图 8.1-7 中的棱锥记作棱锥 . 棱锥的底面可以是三角形、四边形、五边形 ,我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱锥 ,其中三棱锥又叫四面体. 底面是正多边形, 并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.
3. 棱台
定义
如图 8.1-8, 用一个平行于棱锥底面的平面去截棱锥,我们把底面和截面之间那部分多面体叫做棱台(frustum of a pyramid). 图 8.1-1 中的储物箱就给我们以棱台的形象.在棱台中, 原棱锥的底面和截面分别叫做棱台的下底面和上底面. 类似于棱柱、棱锥, 棱台也有侧面、侧棱、顶点.
思考
请你仿照棱锥中侧面、侧棱、顶点的定义,给出棱台侧面、侧棱、顶点的定义, 并在图 8.1-8 中标出它们.
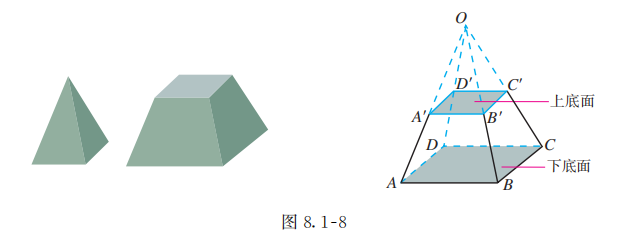
棱台用表示底面各顶点的字母来表示, 如图 8.1-8 中的棱台记作棱台 . 由三棱锥、四棱锥、五棱锥 截得的棱台分别叫做三棱台、四棱台、五棱台
例 1
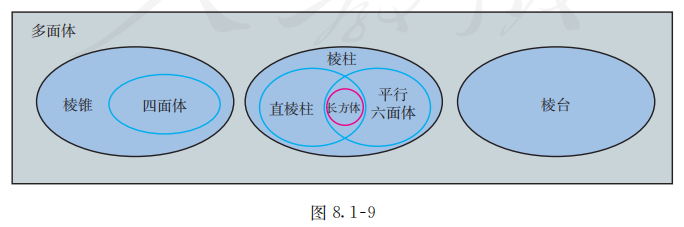
将下列各类几何体之间的关系用 Venn 图表示出来:
多面体, 长方体, 棱柱, 棱锥, 棱台, 直棱柱, 四面体, 平行六面体.
解:
如图 8.1-9 所示.
练习
1.
观察图中的物体, 说出它们的主要结构特征.

2.
判断下列命题是否正确, 正确的在括号内画 “ ”, 错误的画 “ ”.
(1) 长方体是四棱柱, 直四棱柱是长方体.
(2) 四棱柱、四棱台、五棱锥都是六面体.
3.
填空题
(1) 一个几何体由 7 个面围成, 其中两个面是互相平行且全等的五边形, 其他各面都是全等的矩形,则这个几何体是
(2) 一个多面体最少有 个面, 此时这个多面体是 .
4.
设计一个平面图形, 使它能折成一个直三棱柱.
4. 圆柱
定义
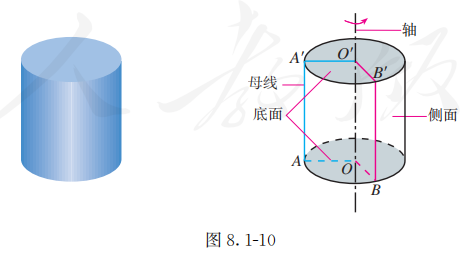
如图 8.1-10, 以矩形的一边所在直线为旋转轴, 其余三边旋转一周形成的面所围成的旋转体叫做圆柱 (circular cylinder). 旋转轴叫做圆柱的轴; 垂直于轴的边旋转而成的圆面叫做圆柱的底面; 平行于轴的边旋转而成的曲面叫做圆柱的侧面; 无论旋转到什么位置, 平行于轴的边都叫做圆柱侧面的母线.
圆柱用表示它的轴的字母表示, 如图 8.1-10 中的圆柱记作圆柱 .
例子
在生活中, 许多物体和容器都是圆柱形的, 如图 8.1-1 中的奶粉罐.
5. 圆锥
定义
与圆柱一样, 圆锥也可以看作由平面图形旋转而成的. 如图 8.1-11, 以直角三角形的一条直角边所在直线为旋转轴, 其余两边旋转一周形成的面所围成的旋转体叫做圆锥 (circular cone).
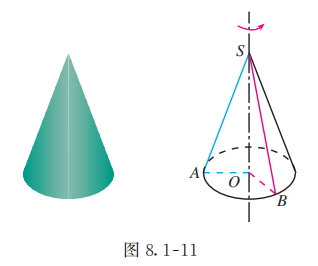
例子
图 8.1-1 中的铅锤就是圆锥形物体.
圆锥也有轴、底面、侧面和母线.
思考
请你仿照圆柱中轴、底面、侧面、母线的定义,给出圆锥的轴、底面、侧面、母线的定义, 并在图 8.1-11 中标出它们.
圆锥也用表示它的轴的字母表示, 如图 8.1-11 中的圆锥记作圆锥 .
6. 圆台
定义
如图 8.1-12, 与棱台类似, 用平行于圆锥底面的平面去截圆锥, 底面与截面之间的部分叫做圆台 (circular truncated cone).
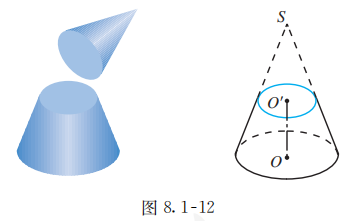
例子
图 8.1-1 中的纸杯就是具有圆台结构特征的物体.
与圆柱和圆锥一样, 圆台也有轴、底面、侧面、母线
思考
(请你在图 8.1-12 中标出它们).
圆台也用表示它的轴的字母表示, 如图 8.1-12 中的圆台记作圆台 .
探究
圆柱可以由矩形旋转得到, 圆锥可以由直角三角形旋转得到. 圆台是否也可以由平面图形旋转得到? 如果可以, 由什么平面图形旋转得到? 如何旋转?
7. 球
定义
如图 8.1-13, 半圆以它的直径所在直线为旋转轴, 旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体 (spheroid), 简称球. 半圆的圆心叫做球的球心; 连接球心和球面上任意一点的线段叫做球的半径; 连接球面上两点并且经过球心的线段叫做球的直径. 球常用表示球心的字母来表示, 如图 8.1-13 中的球记作球 .
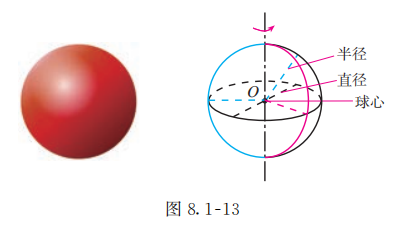
棱柱、棱锥、棱台、圆柱、圆锥、圆台和球是常见的简单几何体. 其中棱柱与圆柱统称为柱体, 棱锥与圆锥统称为锥体, 棱台与圆台统称为台体.
探究
棱柱、棱锥与棱台都是多面体, 它们在结构上有哪些相同点和不同点? 当底面发生变化时, 它们能否互相转化? 圆柱、圆锥与圆台呢?
8. 简单组合体
定义
现实世界中的物体表示的几何体, 除柱体、锥体、台体和球等简单几何体外, 还有大量的几何体是由简单几何体组合而成的, 这些几何体称作简单组合体.
简单组合体的构成有两种基本形式: 一种是由简单几何体拼接而成,如图 8.1-14 (1) (2) 中物体表示的几何体;一种是由简单几何体截去或挖去一部分而成, 如图 8.1-14 (3) (4) 中的几何体. 现实世界中的物体大多是由具有柱体、锥体、台体、球等结构特征的物体组合而成.
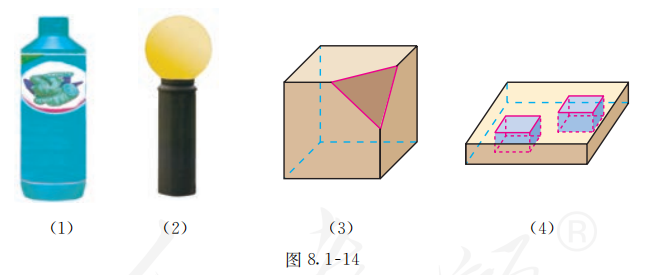
思考
请你说一说图 8.1-14 中各几何体是由哪些简单几何体组合而成的.
例 2
如图 8.1-15 (1), 以直角梯形 的下底 所在直线为轴, 其余三边旋转一周形成的面围成一个几何体. 说出这个几何体的结构特征.
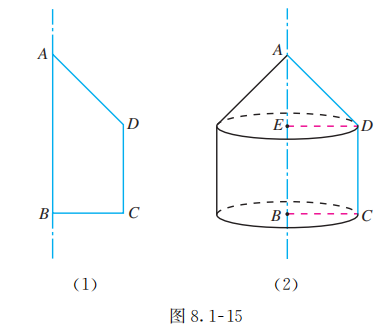
解:
几何体如图 8.1-15 (2) 所示, 其中 , 垂足为 .
这个几何体是由圆柱 和圆锥 组合而成的. 其中圆柱 的底面分别是 和 , 侧面是由梯形的上底 绕轴 旋转形成的; 圆锥 的底面是 , 侧面是由梯形的边 绕轴 旋转而成的.
练习
1.
观察图中的物体, 说出它们的主要结构特征.
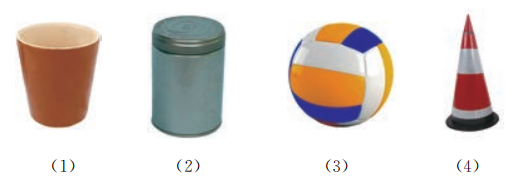
2.
说出图中物体的主要结构特征.

3.
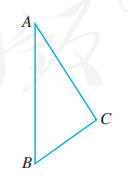
如图, 以三角形 的一边 所在直线为轴, 其余两边旋转一周形成的面围成一个几何体. 说出这个几何体的结构特征.
4.
观察我们周围的物体, 说出这些物体所表示的几何体的主要结构特征.
习题 8.1
复习巩固
1.
如图, 在长方体 中, 指出经过顶点 的棱和面.
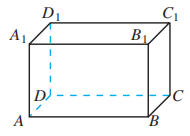
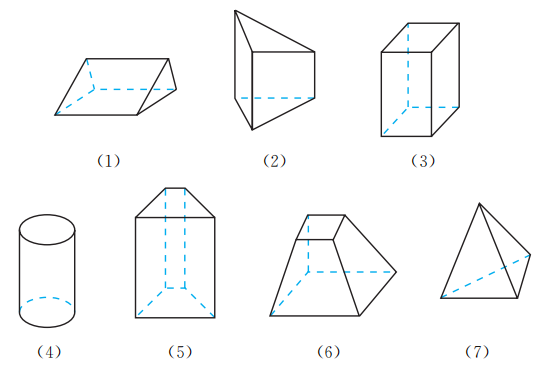
2.
如图, 下列几何体中为棱柱的是 (填写序号).
3.
如图, 汽车内胎可以由下面某个图形绕轴旋转而成, 这个图形是().

4.
如图, 判断下列几何体是不是台体, 并说明为什么.

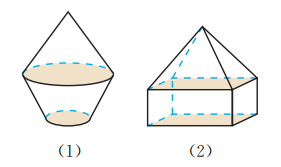
5.
如图, 说出图中两个几何体的结构特征.
综合运用
6.
判断下列命题是否正确, 正确的在括号内画 “ ”, 错误的画 “ ”.
(1) 一个棱柱至少有 5 个面.
(2) 平行六面体中相对的两个面是全等的平行四边形.
(3) 有一个面是平行四边形的棱锥一定是四棱锥.
(4) 正棱锥的侧面是全等的等腰三角形.
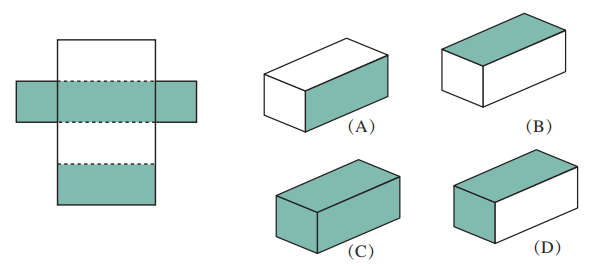
7.
如图, 右边长方体中由左边的平面图形围成的是 .
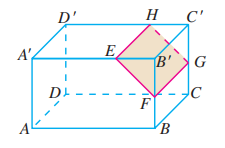
8.
如图, 长方体 被一个平面截成两个几何体, 其中 . 请说出这两个几何体的名称.
9.
如图, 以平行四边形 的一边 所在直线为轴, 其他三边旋转一周形成的面围成一个几何体. 画出这个几何体的图形, 并说出其中的简单几何体及有关的结构特征.
拓广探索
10.
下列命题是否正确? 若正确, 请说明理由; 若错误, 请举出反例.
(1) 有两个面平行, 其他各个面都是平行四边形的多面体是棱柱;
(2) 有两个面平行且相似, 其他各个面都是梯形的多面体是棱台.