4.4 对数函数
2024-02-18 22:09:54 新建
在 4.2 节中, 我们用指数函数模型研究了呈指数增长或衰减变化规律的问题. 对这样的问题, 在引入对数后, 我们还可以从另外的角度, 对其蕴含的规律作进一步的研究.
4.4.1 对数函数的概念
思考
在 4.2.1 的问题 2 中, 我们已经研究了死亡生物体内碳 14 的含量 随死亡时间 的变化而衰减的规律. 反过来, 已知死亡生物体内碳 14 的含量, 如何得知它死亡了多长时间呢? 进一步地, 死亡时间 是碳 14 的含量 的函数吗?
解
根据指数与对数的关系, 由 得到 . 如图 4.4-1, 过 轴正半轴上任意一点 作 轴的平行线, 与 的图象有且只有一个交点 .

这就说明, 对于任意一个 , 通过对应关系 , 在 上都有唯一确定的数 和它对应, 所以 也是 的函数. 也就是说, 函数 刻画了时间 随碳 14 含量 的衰减而变化的规律.
定义 对数函数
同样地, 根据指数与对数的关系, 由 , 且 可以得到 , 且 也是 的函数. 通常, 我们用 表示自变量, 表示函数. 为此, 将 , 且 中的字母 和 对调, 写成 , 且 .
一般地, 函数 , 且 叫做对数函数 (logarithmic function), 其中 是自变量, 定义域是 .
例 1
求下列函数的定义域:
(1) ;
(2) , 且 .
解:
(1) 因为 , 即 , 所以函数 的定义域是
(2) 因为 , 即 , 所以函数 的定义域是
例 2
假设某地初始物价为 1 , 每年以 的增长率递增, 经过 年后的物价为 .
(1) 该地的物价经过几年后会翻一番?
(2) 填写下表, 并根据表中的数据, 说明该地物价的变化规律.

解:
(1) 由题意可知, 经过 年后物价 为
由对数与指数间的关系, 可得
由计算工具可得, 当 时, .
所以,该地区的物价大约经过 14 年后会翻一番.
(2) 根据函数 , 利用计算工具, 可得下表:

由表中的数据可以发现, 该地区的物价随时间的增长而增长, 但大约每增加 1 所需要的年数在逐渐缩小.
练习
1.
求下列函数的定义域:
(1) ;
(2) ;
(3) ;
(4) , 且 .
2.
画出下列函数的图象:
(1) ;
(2) .
3.
已知集合 , 集合 , 下列表达式能建立从集合 到集合 的函数关系的是 _ _ _
(1) ;
(2) ;
(3) ;
(4) .
4.4.2 对数函数的图象和性质
与研究指数函数一样, 我们首先画出其图象, 然后借助图象研究其性质.
例子
不妨先画函数 的图象.
请同学们完成 的对应值表 4.4-1, 并用描点法画出函数 的图象 (图 4.4-2).

思考
我们知道, 底数互为倒数的两个指数函数的图象关于 轴对称. 对于底数互为倒数的两个对数函数, 比如 和 , 它们的图象是否也有某种对称关系呢? 可否利用其中一个函数的图象画出另一个函数的图象?
解
利用换底公式, 可以得到 . 因为点 与点 关于 轴对称, 所以 图象上任意一点 关于 轴的对称点 都在 的图象上, 反之亦然. 由此可知, 底数互为倒数的两个对数函数的图象关于 轴对称. 根据这种对称性, 就可以利用 的图象画出 的图象 (图 4.4-3).
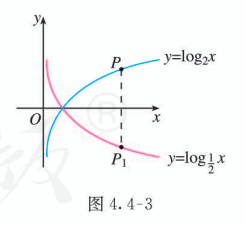
为了得到对数函数 , 且 的性质, 我们还需要画出更多具体对数函数的图象进行观察.
探究
选取底数 , 且 的若干个不同的值, 在同一直角坐标系内画出相应的对数函数的图象. 观察这些图象的位置、公共点和变化趋势, 它们有哪些共性? 由此你能概括出对数函数 , 且 的值域和性质吗?
解
如图 4.4-4, 选取底数 的若干值, 用计算工具画图, 发现对数函数 的图象按底数 的取值, 可分为 和 两种类型. 因此, 对数函数的性质也可以分 和 两种情况进行研究.

对数函数的图象和性质
一般地, 对数函数的图象和性质如表 4.4-2 所示.

例 3
比较下列各题中两个值的大小:
(1) ;
(2) ;
(3) , 且 .
解:
(1) 和 可看作函数 的两个函数值. 因为底数 , 对数函数 是增函数, 且 , 所以
(2) 和 可看作函数 的两个函数值. 因为底数 ,对数函数 是减函数, 且 , 所以
(3) 和 可看作函数 的两个函数值. 对数函数的单调性取决于底数 是大于 1 还是小于 1 , 因此需要对底数 进行讨论.
当 时, 因为函数 是增函数, 且 , 所以
当 时, 因为函数 是减函数, 且 , 所以
例 4
溶液酸碱度的测量.
溶液酸碱度是通过 计量的. 的计算公式为 , 其中 表示溶液中氢离子的浓度, 单位是摩尔/升.
(1) 根据对数函数性质及上述 的计算公式, 说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2) 已知纯净水中氢离子的浓度为 摩尔/升, 计算纯净水的 .
解:
(1) 根据对数的运算性质, 有
在 上, 随着 的增大, 减小,相应地, 也减小, 即 减小. 所以, 随着 的增大, 减小, 即溶液中氢离子的浓度越大, 溶液的酸性就越强.
(2) 当 时, . 所以, 纯净水的 是 7 .
思考
胃酸中氢离子的浓度是 摩尔/升, 胃酸的 是多少?
定义 反函数
前面根据指数与对数间的关系, 由 得 . 由函数定义可知 是一个函数. 这样, 由指数函数 , 可得到对数函数 , 这个对数函数的定义域 、值域 分别是指数函数 的值域和定义域. 这时就说函数 是函数 的反函数 (inverse function).
例子
通常, 我们用 表示自变量, 表示函数. 为此, 把 写成 , 这样, 对数函数 是指数函数 的反函数. 同时, 指数函数 也是对数函数 的反函数. 因此, 指数函数 与对数函数 互为反函数, 它们的定义域与值域正好互换.
探究
对于指数函数 , 你能利用指数与对数间的关系, 得到与之对应的对数函数吗? 它们的定义域、值域之间有什么关系? 它们也互为反函数吗?
解
一般地, 指数函数 , 且 与对数函数 , 且 互为反函数, 它们的定义域与值域正好互换.
练习
1.
在同一直角坐标系中画出函数 和 的图象, 并说明它们的关系.
2.
比较下列各题中两个值的大小:
(1) ;
(2) ;
(3) .
3.
某地去年的 GDP (国内生产总值) 为 3000 亿元人民币, 预计未来 5 年的平均增长率为 .
(1) 设经过 年达到的年 GDP 为 亿元, 试写出未来 5 年内, 关于 的函数解析式;
(2) 经过几年该地 GDP 能达到 3900 亿元人民币?
探究与发现
互为反函数的两个函数图象间的关系
我们知道, 指数函数 , 且 与对数函数 , 且 互为反函数. 它们的图象是否有关系? 有什么关系呢? 下面, 请你运用所学的数学知识和计算工具, 探索几个问题, 亲自发现其中的奥秘吧!
- 在同一直角坐标系中, 画出指数函数 及其反函数 的图象.你能发现这两个函数的图象有什么对称关系吗?
- 取 图象上的几个点, 如 , 关于直线 的对称点的坐标是什么? 它们在 的图象上吗?为什么?
- 如果点 在函数 的图象上, 那么 关于直线 的对称点在函数 的图象上吗? 为什么?
- 根据上述探究过程, 你可以得到什么结论?
- 上述结论对于指数函数 , 且 及其反函数 ,且 ) 也成立吗? 为什么?
4.4.3 不同函数增长的差异
在前面的学习中我们看到, 一次函数与指数函数的增长方式存在很大差异. 事实上,这种差异正是不同类型现实问题具有不同增长规律的反映. 因此, 如果把握了不同函数增长方式的差异, 那么就可以根据现实问题的增长情况, 选择合适的函数模型刻画其变化规律. 下面就来研究一次函数、指数函数和对数函数增长方式的差异.
探究
选取适当的指数函数与一次函数, 探索它们在区间 上的增长差异, 你能描述一下指数函数增长的特点吗?
解
不妨以函数 和 为例.
利用信息技术, 列出上述两个函数的自变量与函数值的对应值表 (表 4.4-3), 并在同一直角坐标系中画出它们的图象 (图 4.4-5). 可以看到, 函数 和 的图象有两个交点 . 在区间 上, 函数 的图象位于 的图象之上, ; 在区间 上, 函数 的图象位于 的图象之下, ; 在区间 上, 函数 的图象位于 的图象之上, . 这表明, 虽然这两个函数在 上都单调递增, 但它们的增长速度不同, 函数 的增长速度保持不变, 而函数 的增长速度在变化.
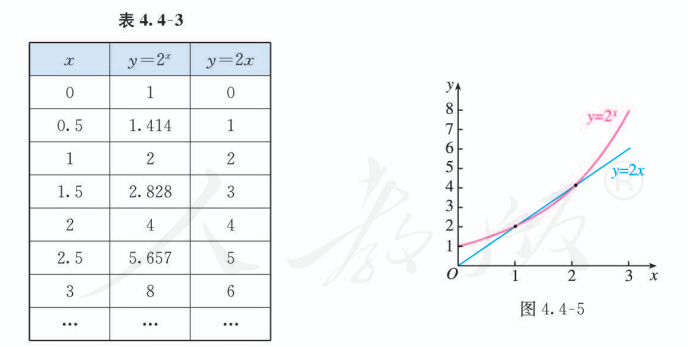
下面在更大的范围内, 观察 和 的增长情况.
从表 4.4-4 和 图 4.4-6 可以看到, 当自变量 越来越大时, 的图象就像与 轴垂直一样, 的值快速增长; 而函数 的增长速度依然保持不变, 与函数 的增长速度相比几乎微不足道.
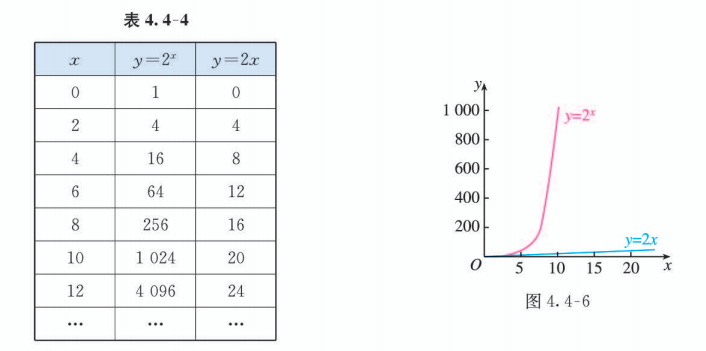
综上所述, 虽然函数 与 在区间 上都单调递增, 但它们的增长速度不同, 而且不在同一个 “档次”上. 随着 的增大, 的增长速度越来越快,会超过并远远大于 的增长速度. 尽管在 的一定变化范围内, 会小于 , 但由于 的增长最终会快于 的增长, 因此, 总会存在一个 , 当 时, 恒有 .
指数函数的爆炸性增长
一般地, 指数函数 与一次函数 的增长差异都与上述情况类似. 即使 的值远远大于 的值, 的增长速度最终都会大大超过 的增长速度.
指数函数不像一次函数那样按同一速度增长,而是越来趟快, 呈爆炸性增长.
探究
选取适当的对数函数与一次函数, 探索它们在区间 上的增长差异, 你能描述一下对数函数增长的特点吗?
解
不妨以函数 和 为例.
利用信息技术, 列出上述两个函数的自变量与函数值的对应值表 (表 4.4-5), 并在同一直角坐标系中画出它们的图象 (图 4.4-7). 可以看到, 虽然它们在 上都单调递增, 但增长速度存在着明显的差异. 函数 的增长速度保持不变, 而 的增长速度在变化. 随着 的增大, 函数 的图象离 轴越来越远, 而函数 的图象越来越平缓, 就像与 轴平行一样. 例如 ; 而 . 这说明,当 , 即 时, 与 相比增长得就很慢了.
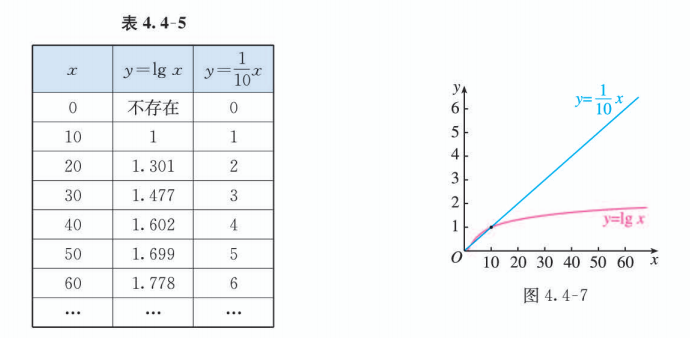
思考
如果将 放大 1000 倍, 再对函数 和 的增长情况进行比较, 那么仍有上述规律吗?
对数函数的平缓增长
一般地, 虽然对数函数 与一次函数 在区间 上都单调递增, 但它们的增长速度不同. 随着 的增大, 一次函数 保持固定的增长速度, 而对数函数 的增长速度越来越慢. 即使 的值很小, 在一定范围内, 可能会大于 , 但由于 的增长最终会慢于 的增长, 因此总会存在一个 , 当 时, 恒有 .
对数函数比较适合于描述增长速度平缓的变化规律.
探究
类比上述过程,
(1) 画出一次函数 , 对数函数 和指数函数 的图象, 并比较它们的增长差异;
(2) 试着概括一次函数 , 对数函数 和指数函数 的增长差异;
(3) 讨论交流 “直线上升” “对数增长” “指数爆炸” 的含义.
练习
1.
三个变量 随变量 变化的数据如下表:

其中关于 呈指数增长的变量是 _ _ _ .
2.
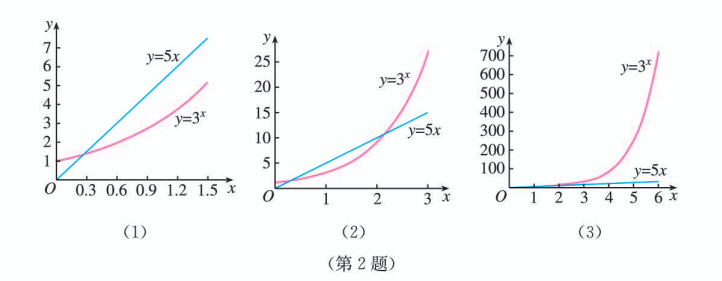
(1) (2) (3) 分别是函数 和 在不同范围的图象, 借助计算工具估算出使 的 的取值范围(精确到 0.01 ).
3.
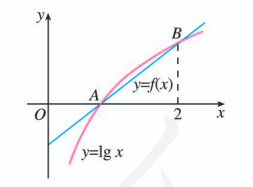
如图, 对数函数 的图象与一次函数 的图象有 两个公共点. 求一次函数 的解析式.
4.
函数 的图象如图所示, 则 可能是 ( ).
(A)
(B)
©
(D)

习题 4.4
复习巩固
1.
求下列函数的定义域:
(1) ;
(2) .
2.
比较满足下列条件的两个正数 的大小:
(1) ;
(2) ;
(3) ;
(4) .
3.
在不考虑空气阻力的条件下, 火箭的最大速度 (单位: ) 和燃料的质量 (单位: )、火箭 (除燃料外) 的质量 (单位: ) 的函数关系是 . 当燃料质量是火箭质量的百分之几时, 火箭的最大速度可达到 ?
4.
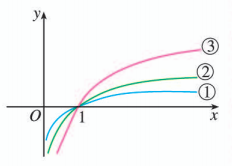
函数 的图象如图所示,
(1) 试说明哪个函数对应于哪个图象, 并解释为什么;
(2) 以已有图象为基础,在同一直角坐标系中画出 , 的图象;
(3) 从(2)的图中你发现了什么?
5.
大西洋鲑鱼每年都要逆流而上, 游回产地产卵. 研究鲑鱼的科学家发现鲑鱼的游速 (单位: ) 可以表示为 , 其中 表示鱼的耗氧量的单位数.
(1) 当一条鱼的耗氧量是 2700 个单位时, 它的游速是多少?
(2) 计算一条鱼静止时耗氧量的单位数.
6.
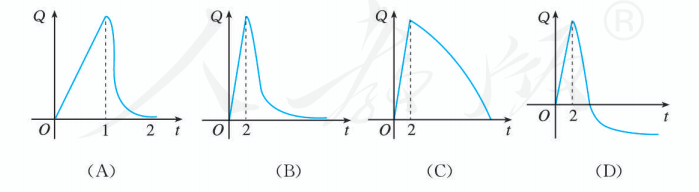
在 内将某种药物注射进患者的血液中. 在注射期间, 血液中的药物含量呈线性增加; 停止注射后, 血液中的药物含量呈指数衰减. 能反映血液中药物含量 随时间 变化的图象是 ( ).
综合运用
7.
判断下列各对函数是否互为反函数. 若是, 则求出它们的定义域和值域:
(1) ;
(2) .
8.
设 表示摄氏温度为 时, 华氏温度为 ,
(1) 如果函数 的反函数是 , 那么 表示什么?
(2) 如果 , 那么求 , 并说明其实际意义.
9.
某地由于人们健康水平的不断提高, 某种疾病的患病率正以每年 的比例降低. 要将当前的患病率降低一半, 需要多少年?
10.
声强级 (单位: dB) 由公式
给出, 其中 为声强 (单位: ).
(1) 一般正常人听觉能忍受的最高声强为 , 能听到的最低声强为 . 求人听觉的声强级范围.
(2) 平时常人交谈时的声强约为 , 求其声强级.
11.
假设有一套住房的房价从 2002 年的 20 万元上涨到 2012 年的 40 万元. 下表给出了两种价格增长方式, 其中 是按直线上升的房价, 是按指数增长的房价, 是 2002 年以来经过的年数.
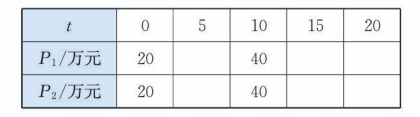
(1) 求函数 的解析式;
(2) 求函数 的解析式;
(3) 完成上表空格中的数据, 并在同一直角坐标系中画出两个函数的图象, 然后比较两种价格增长方式的差异.
拓广探索
12.
已知 , 求实数 的取值范围.
13.
比较下列各题中三个值的大小:
(1) ;
(2) .